基于异构并行计算的单细胞测序数据聚类算法
谢林娟,李荔瑄,张少强
天津师范大学 计算机与信息工程学院,天津 300387
在过去的几年里,为了人类健康以及诊断、监测和治疗疾病,单细胞RNA测序(scRNA-seq)相关的研究得到了迅速的发展。包含数十万甚至上百万个单细胞测序数据的多个图谱项目相继完成[1-2]。这些项目主要归功于单细胞测序技术的发展。目前主流的测序平台能够一次完成数千到数万个细胞的测序[3]。但是,由于测序手段的限制以及基因表达高度复杂等原因,scRNA-seq数据普遍存在噪声较大、维度较高、稀疏性较强等特点[4]。细胞分型是单细胞数据分析的重要流程之一[5]。现在主流的细胞分型方法先运用主成分分析(principal component analysis,PCA)、t分布随机近邻嵌入(t-dis‐tributed stochastic neighbor embedding,t-SNE)或均匀流形近似和投影(uniform manifold approximation and projection,UMAP)[6]等经典数据降维方法进行数据降维或者进行特征选择,然后采用DBSCAN、谱聚类、层次聚类、K-means等经典聚类方法进行分型。例如SC3[7]运用PCA和t-SNE降 维及K-means进行 一 致性聚类;CI‐DR[8]运用PCA降维和层次聚类;SCENA先特征选择再谱聚类[9]。在几千细胞的小规模测序数据,这些算法均具有良好的性能。
目前针对大规模单细胞RNA测序数据的聚类基本采用构建简单的细胞关系网络,并对该网络运用社区检测的算法(例如鲁汶算法[10])来进行。而谱聚类和层次聚类算法受限于计算复杂性,很难应用于大数据集。PhenoGraph[11]需要是先构造k最近邻(k-nearest neigh‐bors,KNN)图然后对每一对细胞的共享最近邻居(shared nearest neighbors,SNN)重新加权再用鲁汶社区检测算法聚类。SCANPY[12]基于UMAP降维后构造KNN图再调用PhenoGraph聚类。DropClust[13]使用了对数时间的局部敏感哈希(locality sensitive hashing,LSH)算法来确定每个细胞的近似KNN,然后用鲁汶算法聚类。PARC[14]用对数时间复杂性的“分层导航小世界”(hierarchical navigable small world,HNSW)[15]搜索每个细胞的近似KNN,然后用莱顿模块优化(Leiden modularity optimization)[16]的社区检测算法进行聚类。这些大规模聚类工具大都通过近似构造KNN图来提高计算速度。虽然基于社区检测的莱顿算法和鲁汶算法能够保证计算速度,但是其准确度低于其他聚类算法[17-18]。scAIDE[19]是一个先用自动编码器插补和降维,然后用随机投影哈希(random projection hashing,RPH)初始化聚类质心(centroid)来加速k-means的方法,该工具可以快速处理大规模数据,但需要事先确定类簇数目。
因此如果能够构造更符合细胞关系的网络图并能够在聚类过程中自动确定类簇数目,将能够提升单细胞数据的聚类准确度。此外,在聚类之前耗费时间最长的是计算细胞间的相似度。为此,本文结合openMP和CUDA来进行CPU+GPU的异构并行计算,并采用KNN和细胞相似度阈值相结合的方法构建相似网络,最后通过改进马尔可夫聚类算法(Markov clustering,MCL)[20]来进行快速聚类。该算法命名为SCMC(single-cell Markov clustering),其C++代码在Github开源共享,其代码及算法说明文档详见https://github.com/shaoqiang‐zhang/SCMC/。
1 方法与数据
1.1 方法概述
给定由细胞集合C组成的单细胞表达矩阵X,其中m为基因数,n为细胞数。SCMC首先对输入表达矩阵X的每个细胞的元素进行标准化处理;然后计算所有基因的变异系数,并根据变异系数阈值进行特征基因的选择;再运用并行计算技术计算细胞之间的相似度构建细胞相似网络;最后通过采用修改的马尔科夫聚类算法对细胞相似度网络进行快速聚类,得到细胞类型。算法流程见图1,具体方法步骤见1.2节至1.5节描述。
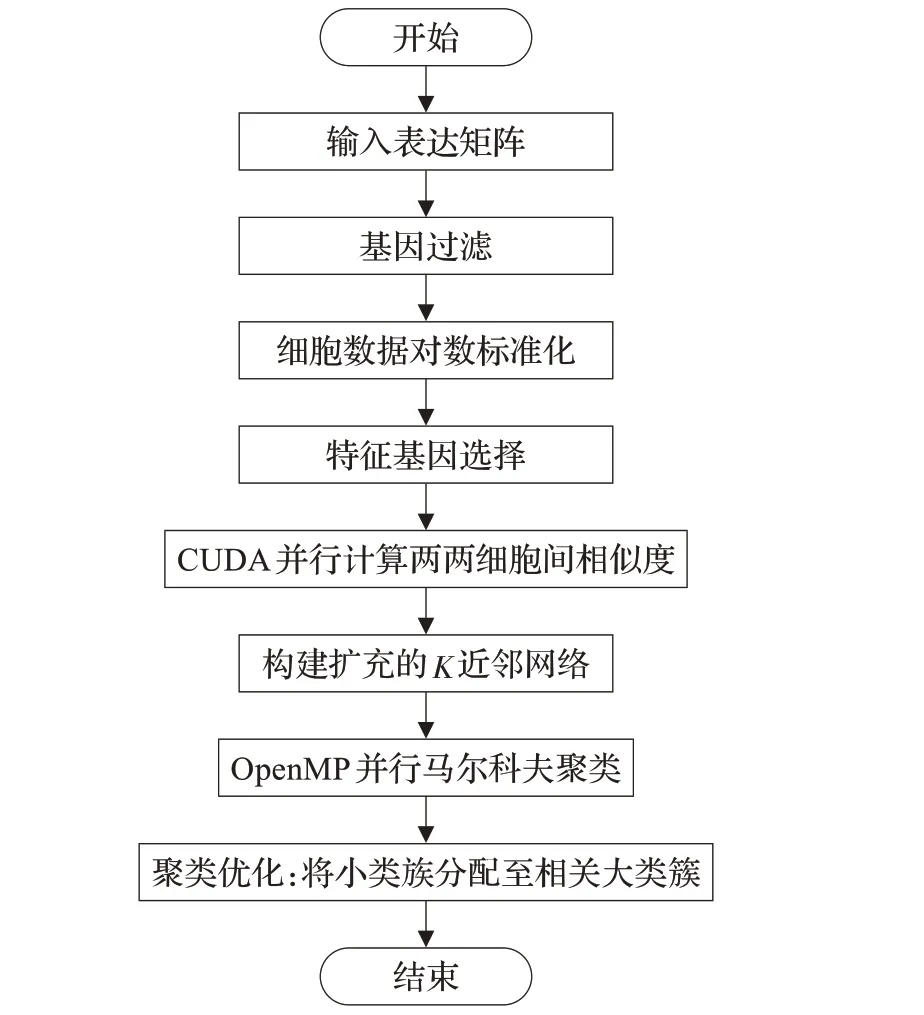
图1 SCMC算法流程图Fig.1 Flow chart of SCMC
1.2 数据预处理和特征基因选择
数据预处理分为以下两个步骤:基因过滤和细胞数据对数标准化(log-normalization)。即先从X中移除在所有细胞表达值均为0的基因(行),然后对矩阵的每个元素除以该元素所在细胞列的元素总和再乘以一个比例因子(默认为10 000),最后加上伪数1取对数,见公式(1):

对对数标准化后的矩阵(x'ij),计算每个基因的变异系数(coefficient of variation)。变异系数为基因所在行元素的标准差除以均值。根据所有基因变异系数的长尾分布(heavy-tailed)曲线设置变异系数变化趋缓的长尾阈值α,根据阈值α选取变异系数最大的前T个基因作为特征基因。注意不同的数据集会选择不同的阈值,从而选择不同数量的特征基因。
1.3 计算细胞相似度构建扩充的K近邻网络
构建K近邻(K-nearest neighbors,KNN)网络是目前多数大规模细胞聚类的通用方法。在构建KNN网络之前,需要计算降维后的两两细胞对应特征表达向量的欧氏距离。设细胞i和j对应的特征基因的表达向量分别为x和y,按照公式(2)计算两细胞之间的余弦相似度。

根据公式(3)的推导,计算标准化后两向量的欧氏距离D等价于计算向量的余弦距离[21]。余弦相似度相当于对细胞的特征表达向量做了标准化处理再求欧氏距离D,因此无需对降维后的细胞表达向量再标准化。
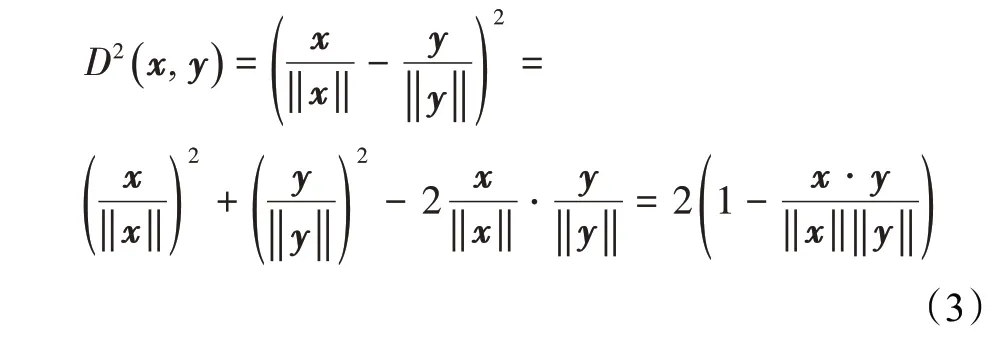
因为计算一对细胞的余弦相似度不需要与别的细胞交换信息,因此将n个细胞的所有可能的C2n种细胞对(cell pairs)组合分配到GPU的所有k个内核上进行CUDA并行计算。这样理论上比CPU单线程的运算提高k倍。
对每个细胞x,计算x与其他所有细胞间的余弦相似度,并保留相似度最高的前条边集合Nx和相似度超过阈值β的边集Bx,得到与顶点x关联的边集Nx⋃Bx。由此构造扩充的K近邻网络(expanded KNN),其中顶点集合为细胞集合C,边集为
1.4 马尔科夫聚类算法的并行实现
运用马尔科夫聚类(Markov clustering,MCL)算法对扩充的KNN网络进行聚类。MCL算法是van Dongen[20]开发的基于图的聚类的算法,主要思想是通过概率状态转移矩阵进行随机游走(random walk)。该算法不需预先设定聚类数目,通过反复修正矩阵以实现随机流模拟。
首先根据细胞相似网络构造邻接矩阵,然后对邻接矩阵进行标准化,即每个矩阵元素除以所在列的所有元素之和得到概率转移矩阵,如公式(4):

构造邻接矩阵每列元素的概率用不到其他列的信息,因此针对每列进行并行化设计(即矩阵每列指派不同的线程处理)。MCL算法是“扩展”(Expansion)操作和“膨胀”(Inflation)操作交替重复执行的过程。首先将概率矩阵进行扩展操作,对矩阵N*进行p次幂方得到矩阵M如公式(5):

随即进行膨胀操作,对矩阵M内元素进行r次幂方得到矩阵G,如公式(6):

判断矩阵G与扩展操作前的矩阵N*是否非常接近,即矩阵G与N*所有相同位置元素之差小于规定的误差ε(例如ε=10-4),则收敛,输出聚类结果;否则令N*=G继续迭代执行扩展操作和膨胀操作直至收敛。
在实际聚类中,设置p=2,r=1.5。其中扩展操作(公式(5))实际就是矩阵的乘法运算,矩阵被按行和列分块进行并行计算;而膨胀操作(公式(6))与(公式(4))类似的并行设计,即对G的每列进行并行化处理。本文调用openMP并行库(https://www.openmp.org/)来并行化MCL的C++代码。
1.5 马尔科夫聚类的改进
原始的马尔科夫聚类结果常常会产生规模很小的类簇,甚至只包含一个顶点的孤立点簇(统称“小类簇”)。对于较大规模的单细胞数据,这些小类簇应该不是新的细胞类型。为此,为了提高聚类的准确度,SCMC将小类簇重新分配到其他类簇(统称“大类簇”)中。对每个小类簇S,在扩充的KNN网络中标记与该小类簇每个顶点s∈S关联的相似度最高的顶点所属的大类簇编号l(s);从而得到小类簇S关联度最高的大类簇编号集合L(S)={l (s),s∈S}。取L(S)中出现频次最高的大类簇作为S的最终目标类簇,将S分配给该类簇。如果n中存在多个频次最高的大类簇,则选择与S中所有顶点相似度最高的顶点所属类簇。
1.6 数据集和评估指标
为了测试算法的性能,本文选取7个较大规模具有代表性的单细胞测序数据集(依次编号Data1~Data7)。这些数据集分别从基因表达综合数据库(gene expres‐sion omnibus,GEO)和10X Genomics官网(https://www.10xgenomics.com/resources/datasets)免费获取。Data1为3 005个小鼠大脑皮层(cerebral cortex)细胞scRNA-seq数据集(GEO编号:GSE60361)[22];Data2为10X Genom‐ics的4 340个健康人体外周血单核细胞(peripheral blood mononuclear cells,PBMCs)数据集;Data3、Da‐ta4、Data5分别为三个混合人体HEK293T细胞和小鼠NIH3T3细胞的数据集(样本标识分别为10k_hgmm_3p、10k_hgmm_3p_nextgem_Chromium_X 和20k_hgmm_5pv2_HT_nextgem_Chromium_X);Data6为24 822个 小鼠前额叶皮层(prefrontal cortex)细胞数据集(GEO编号:GSE124952)[23];Data7为68 579个健康人体外周血单核细胞(peripheral blood mononuclear cells,PBMCs)数据集。实验所用数据集的具体信息见表1。
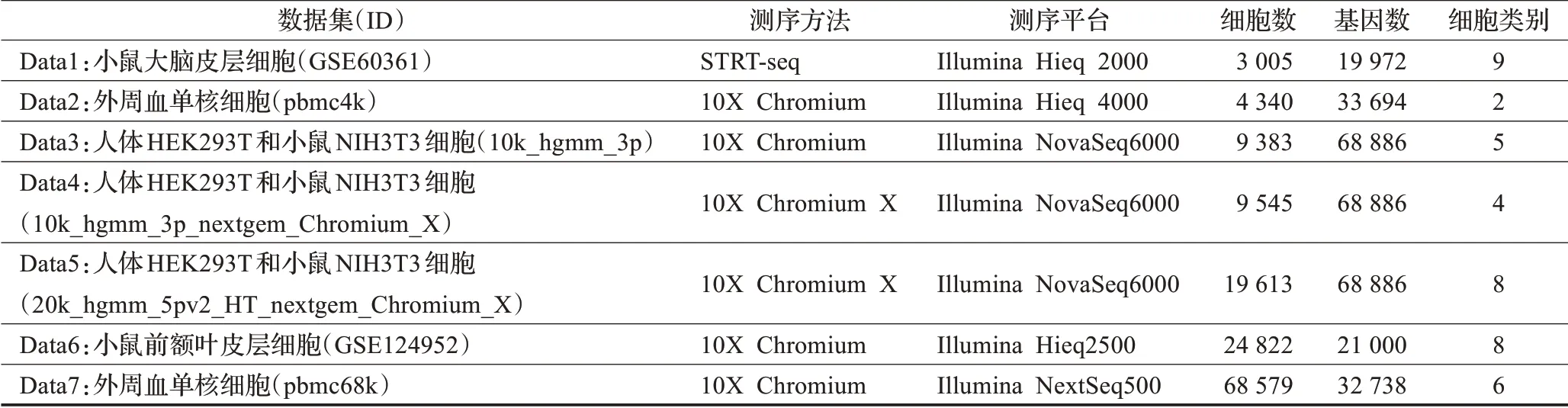
表1 实验数据集Table 1 Experimental data set
调整兰德系数(adjusted Rand index,ARI)[24]被广泛用于评估单细胞数据聚类效果[25]。给定n个目标(细胞)的聚类结果X=( )X1,X2,…,Xr和真实划分结果调整兰德系数的定义如公式(7):
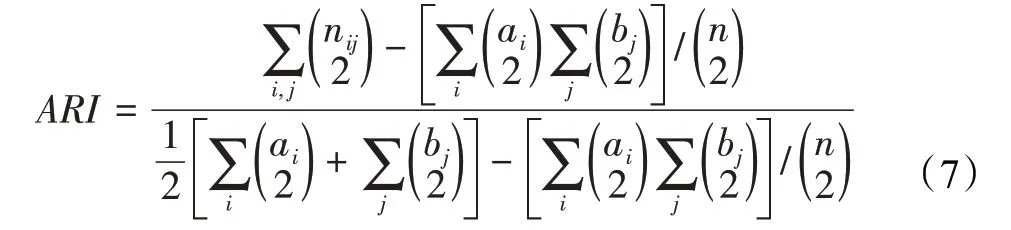
其中,nij代表Xi和Yj中均有的目标数目,ai和bj分别表示在Xi和Yj中的细胞数目。
1.7 方法选择和参数设置
在大规模单细胞聚类中应用最广泛的是SEURAT4[26],该工具均直接调用PhenoGraph中的鲁汶算法进行聚类。SCENA是最新的单细胞聚类算法,该方法基于多特征选择的谱聚类算法并声明在大多数实验数据上优于SEURAT4和SC3等主流工具[9]。本文重点将SCMC与SCENA和SEURAT4,以及另一基于鲁汶算法的工具SCANPY进行比较。所有比较工具的参数均采用默认参数,其中KNN的参数K均设置为相同值。单细胞数据的预处理(包括对数标准化和删除低表达基因等)均按照各个工具默认参数进行。所有程序均在Linux工作站(CPU为Intel Xeon E5-2620/2.10 GHz/8×2 cores,GPU为NVidia GTX1080Ti)上运行。
2 方法与数据
2.1 扩充KNN网络提高聚类效果
以前的方法大都根据细胞相似性构建KNN网络或者近似KNN网络,然后对网络图进行聚类。直接用KNN网络进行聚类效果并不理想,单纯KNN网络没有充分考虑细胞之间的相似度。一对高度相似表达的细胞因为数目K的限制,可能在KNN图中没有直接连接,因此通过保留高相似度(相似度>0.95)的连接来扩充KNN网络。如表2所示,分别在7个单细胞数据集上构造单纯的KNN网络与扩充的KNN网络并进行后续聚类步骤,发现对大部分数据集,在扩充KNN网络的聚类比在单纯KNN网络上聚类效果显著增强。只有Data2数据集效果没有显著变化,这可能该数据集本身容易聚类(ARI=0.974)。而在Data6数据集上扩充的KNN网络比单纯的KNN提升效果非常显著。
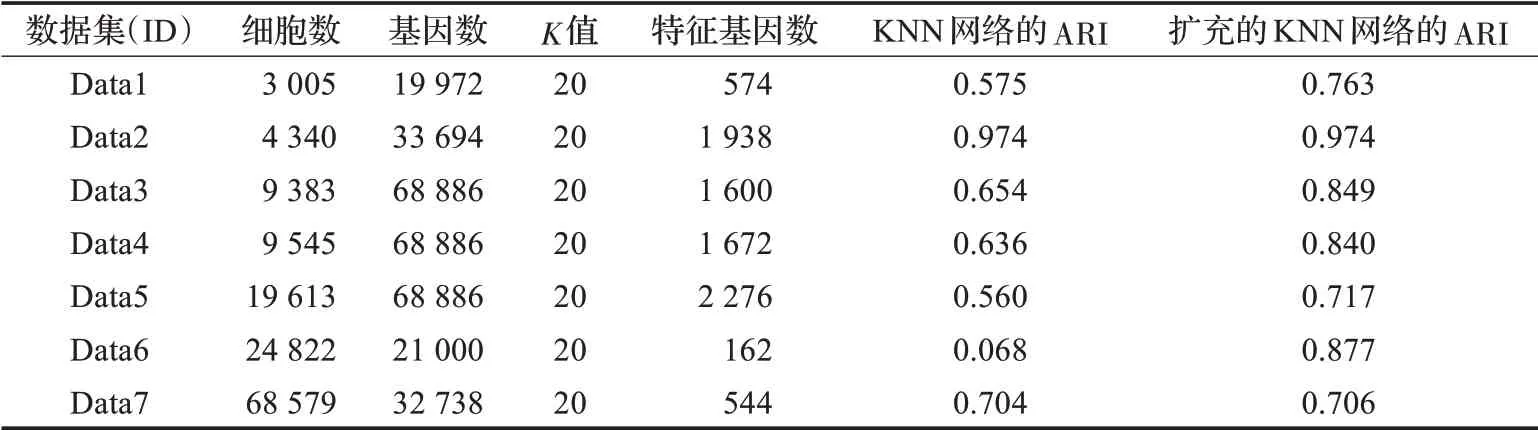
表2 KNN网络与扩充KNN网络实验比较Table 2 Experimental comparison between KNN networks and extended KNN networks
SCMC算法的主要参数指标是KNN中的最近邻数K。选取三个不同规模的数据(Data2、Data4和Data6)来验证不同K值对最终结果的影响。分别选取K=10、20、30、40,然后进行聚类并计算ARI。如图2所示,在这三个数据中SCMC算法的主要参数指标是KNN中的最近邻数K。如图2所示,在这三个数据集中,K≥20表现比较平稳,其中最大的数据集Data6,随着K增大ARI也相应也有所增加。但K越大,KNN网络的密度就会增大,算法复杂性就会增高。为此在所有较大规模数据集,为了减少算法复杂度,建议K设置为20。
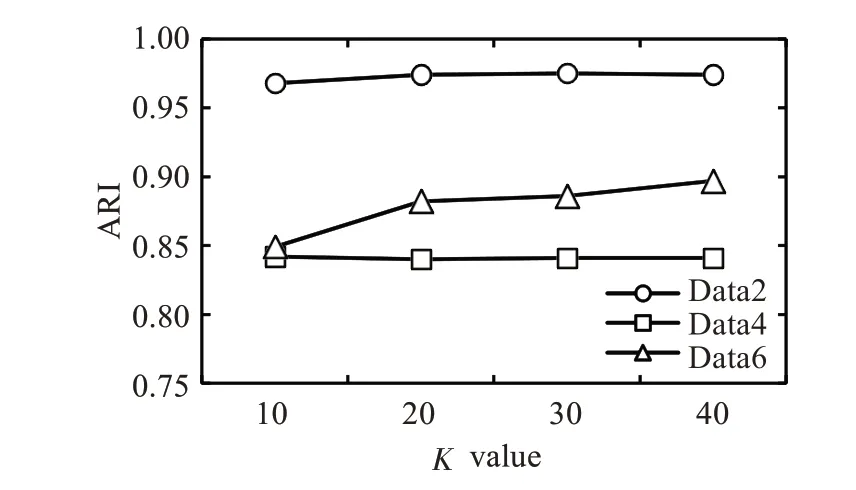
图2 不同K值对ARI的影响Fig.2 Effect of different K values on ARI
聚类算法前的特征基因选择也会影响最终的聚类结果,SCMC算法通过计算基因的变异系数(coefficient of variation)来选择高可变的基因作为特征基因。图3是7个数据集基因变异系数的分布曲线,这些曲线的形态基本一致;变异系数越高的基因越可能是特征基因,根据帕累托法则(Pareto principle),重尾(heavy-tailed)部分大概率是特征显著的基因。由于帕累托分布(Pareto distribution)属于重尾连续概率分布,与图3的曲线形态基本一致,为此,SCMC用帕累托分布来拟合基因变异系数的分布曲线(可以选用fitdistrplus的R包实现),选取面积占比5%的重尾部分的高可变基因作为特征基因,如图3所示。在算法实际运行中,也可以观测曲线选择变化开始趋缓的值作为特征基因选择的阈值(例如:曲线a点的值v(a)小于下一点a+1值v( a+1)的2倍,v(a)<2v( a+1),则取值a为阈值来选择特征基因)。
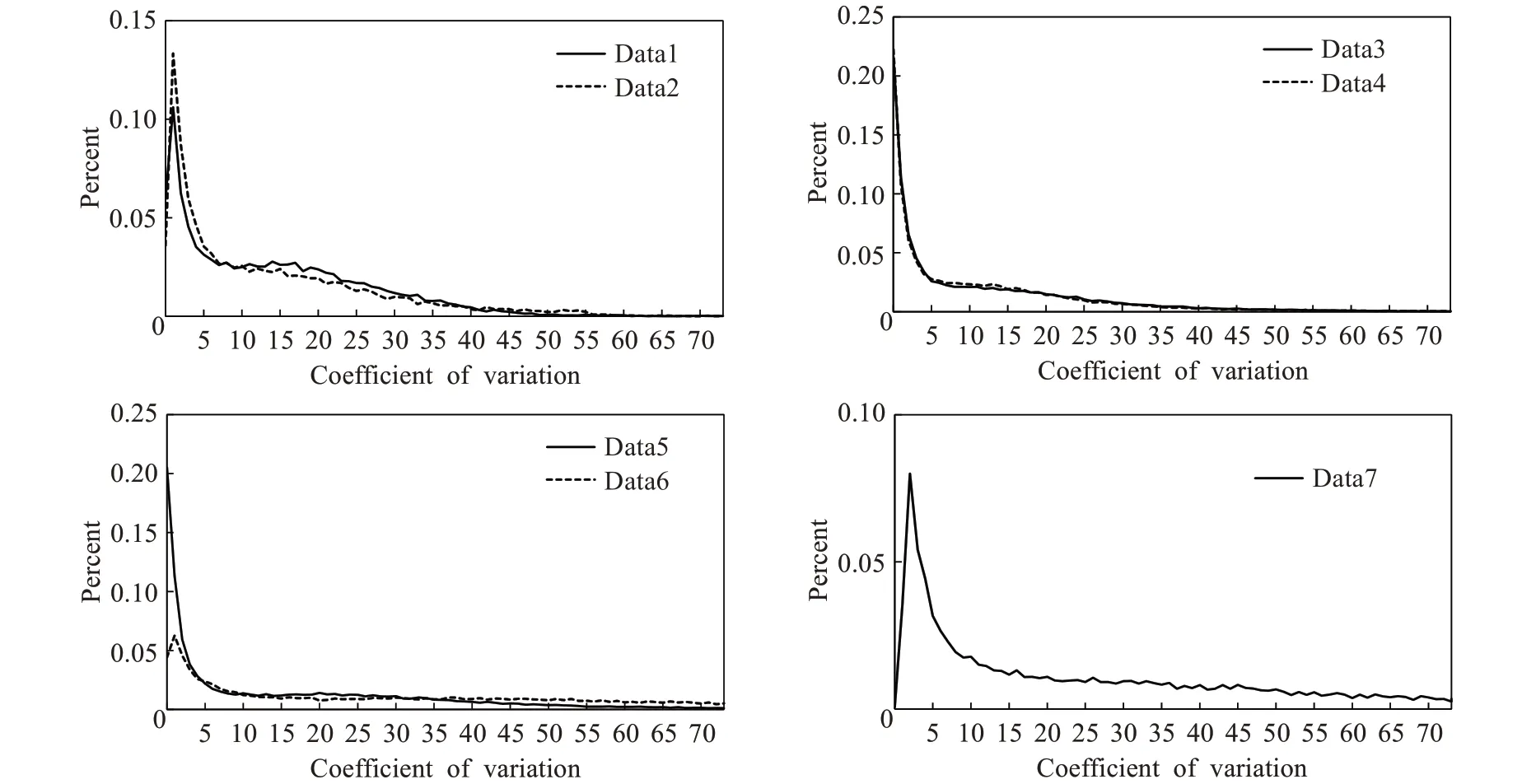
图3 各数据集基因变异系数分布曲线Fig.3 Distributi on curveDsa tao 5f coefficien of gene variation for 7 datasets
2.2 改进MCL以提高聚类效果
MCL算法是经典的图聚类算法,该算法已经被成功应用到模体聚类等研究领域。当数据规模很大的时候,该算法复杂性较高( O(n2))以及容易产生大量的离群孤立或者小规模类簇,因此在单细胞聚类中,首先对MCL算法进行openMP并行设计来加快算法,另外对MCL算法产生的孤立点和小类簇进行再分配,以提升聚类效果。
实验中将类簇规模小于3的进行再分配。如表3所示,分别比较了改进前和改进后MCL聚类的ARI结果。除了Data2、Data3和Data4的ARI没有明显变化,算法在其他数据上ARI指标均有所增加。说明对MCL的改进能够提升聚类的效果。另外,改进后的MCL聚类得到的类簇数与数据集提供的细胞类别数比较接近。对于Data7,改进后MCL的聚类结果的类簇数大幅度减少,由此可以看出算法对于大规模数据类簇数减少明显,说明MCL本身产生了较多的小类簇。
2.3 并行异构计算加速聚类算法
由于SCMC没有对细胞的特征基因进行降维,而直接计算细胞之间的相似度,因此计算细胞之间相似度并构建扩充的KNN图会占用大量的计算时间。为此,SCMC通过CUDA并行化来计算细胞相似度,通过openMP并行化MCL聚类来加快算法。从Data7中随机取样不同固定数量的细胞(从4 000到24 000个细胞)样本来分别评估SCMC在CPU+GPU异构并行的运行时间。如果单纯用30个线程的CPU,4 000个细胞就耗时十几个小时。但是如图4所示,如果采用CPU(30线程)+GPU异构计算,对于24 000个细胞的大规模数据集,SCMC的运行时间仅用时0.87 h。对于4 000个细胞的数据集,SCMC的运行时间则仅需要8 min左右。
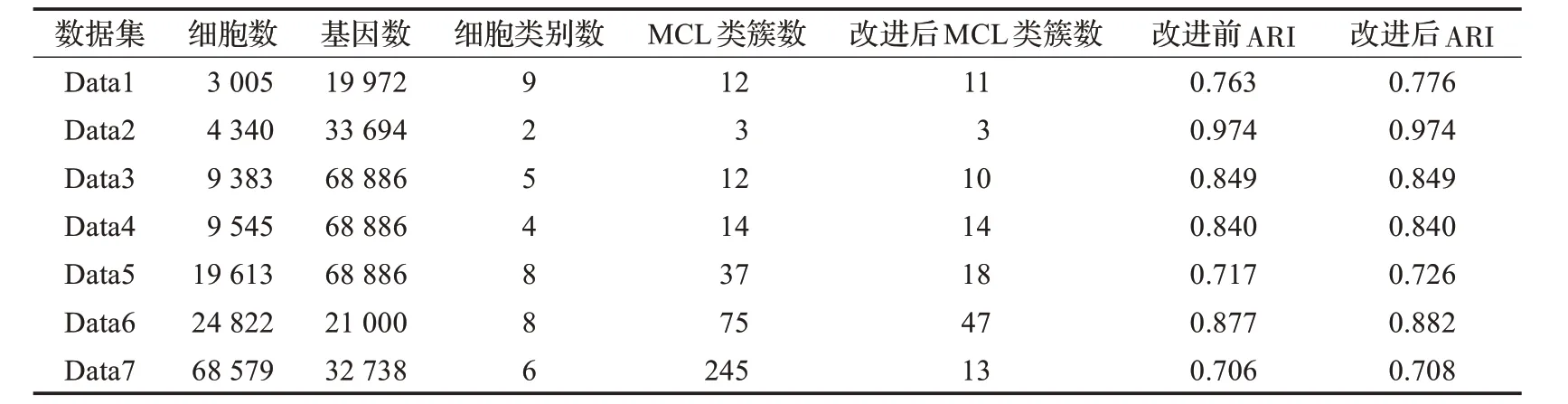
0.05表3 MCL改进前后聚类结果比较Table 3 Comparison of clustering results before and after MCL improvement
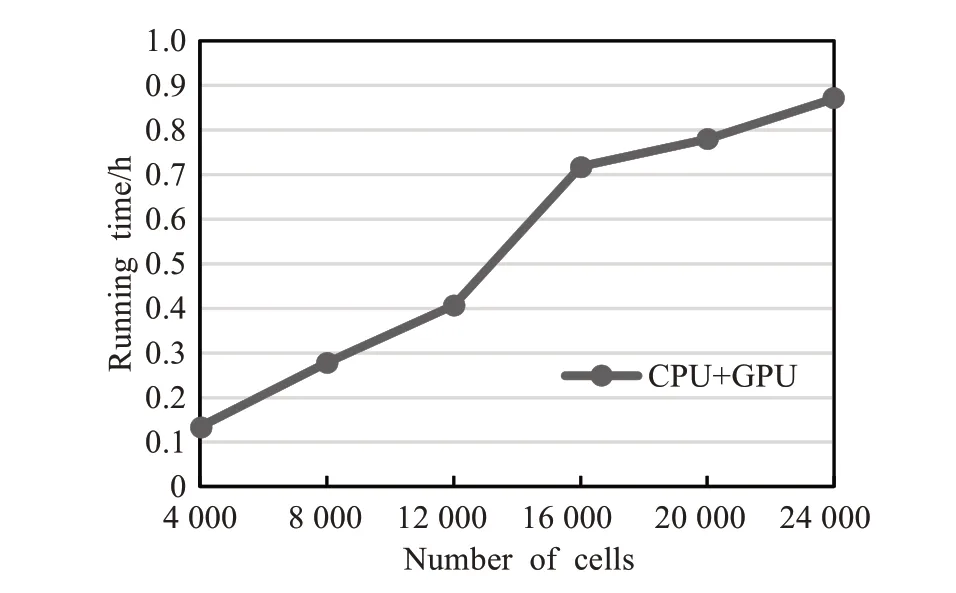
图4 SCMC算法不同细胞数量的运行时间Fig.4 Running time of SCMC on different numbers of cells
2.4 SCMC与其他聚类方法的性能比较
将SCMC与2种最流行的算法SEURAT4和SCANPY,以及最新聚类算法SCENA进行性能比较。分别用这4个工具对表1的7个数据集进行聚类,并计算聚类的ARI指标。
如图5所示,SCMC的 ARI 指标在这些工具中始终表现最好,特别是SCMC在所有测试数据上的 ARI 均大于0.7,算法具有较好的鲁棒性。由于SCMC在大部分实验数据上要比其他三个算法更接近真实类簇(细胞类型)数目,因此反映在ARI指标上要优于其他算法。因为SCANPY和SEURAT4均使用社区检测算法,在默认聚类粒度参数下,大都属于粗粒度聚类,因此得到类簇数与实际细胞类型数相差较大。SCENA采用谱聚类,并用近邻传播聚类估计类簇数。在Data6数据集上SCENA预测的聚类数是14,更接近真实聚类数目,由此SCMC与SCENA的ARI指标比较接近。但在其他测试数据上性能较明显低于SCMC,说明SCENA的鲁棒性较差SCANPY聚类。
作为无监督聚类方法,SCMC在聚类中无须在聚类前估计细胞类簇的数目。虽然SCMC输出的类簇数与数据本身提供的类簇数有所出入,但是较高的ARI指标说明SCMC可能是对大类细胞进行了亚群的细分。例如,SCMC 预测 Data7 数据(pbmc68K)有 13 个细胞类型,接近其真实的 11 个细胞亚型。再如图 6 所示,对Data2数据的聚类结果通过UMAP降维后取前两维作图发现,SCMC聚类标签与原始标签吻合度最高,并且发现右下角存在稀有细胞类型,但在原始标签中该部分被分到了距离较远的细胞类型中。从图6(c)、(d)、(e)可以看出另外三个聚类算法可视化的聚类标签比较杂乱。此外,SCMC算法另一优点是占用内存低。在构建扩充KNN图的时候,通过CUDA将每一对细胞分别输入到GPU计算单元,计算每对细胞的相似度后自动释放内存,因此SCMC算法在计算细胞相似性时候只占用小量GPU存储,而其他基于矩阵运算的算法(例如SCENA等)基本要一次读入所有细胞数据,占用大量的内存。
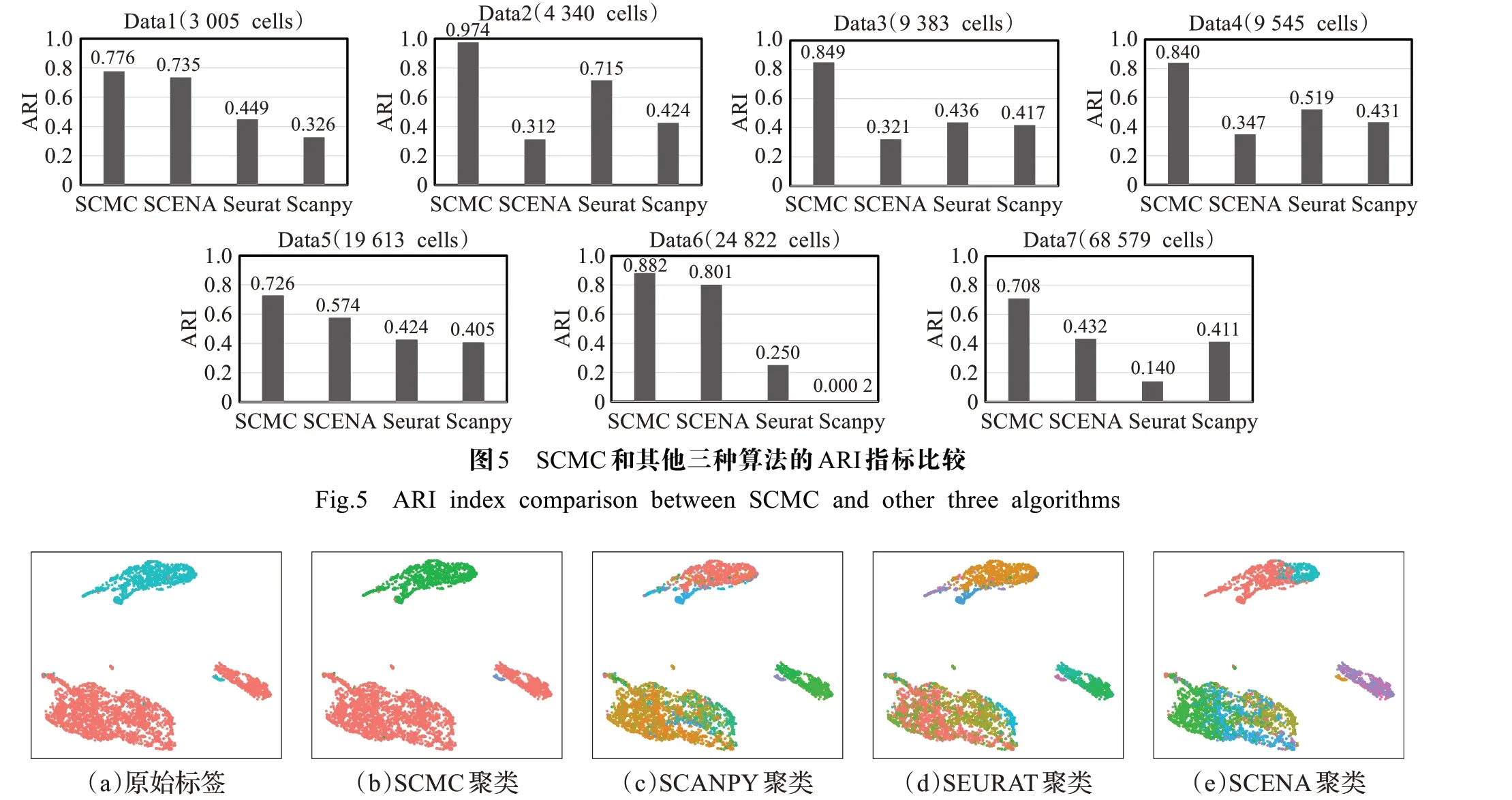
图6 UMAP降维后Data2数据集的可视化结果Fig.6 Clustering visualization effects of Data2 after UMAP dimensionality reduction
3 结论与展望
SCMC算法将扩充的KNN网络与改进的MCL聚类算法进行结合,并且基于CPU+GPU进行并行化程序设计,因此适用于规模较大的单细胞RNA测序数据的细胞分类。通过在7个10X单细胞测序数据上实验比较,算法比其他几个最流行的算法聚类效果要好,因此该算法比较适用于10X单细胞数据分析。

