基于MED和WMSDL的滚动轴承内圈故障特征诊断
周余成, 高哲瑜, 沈丹峰, 梁昌艺
(西安工程大学 机电工程学院, 陕西 西安 710048)
轴承广泛应用于各行各业,其磨损信号和磨损机理越来越受研究者的关注。点蚀和表面剥落是滚动轴承最常见的损伤类型,由两接触物发生相对滑动时产生摩擦造成的,不可逆转。
摩擦根据摩擦形式不同可分为:内摩擦和外摩擦、静摩擦和动摩擦、滑动摩擦和滚动摩擦等。根据接触面有无润滑的情况,滑动摩擦可分为:干摩擦、边界摩擦、流体摩擦和混合摩擦[1]。不同摩擦形式对机械设备零部件损伤程度不同,因此摩擦的检测及类型判别对设备零部件寿命预测及磨损程度识别具有非常重要的意义。
常用故障诊断方法有润滑油温度检测、油样分析和振动检测等。这些方法能提取故障特征,也存在局限性:润滑油温度检测存在温度滞后效应;油样分析只适用于油润滑轴承;振动检测方法易受环境噪声干扰,导致故障特征频率不易提取[2]。
在滚动轴承振动信号特征提取方面,唐贵基等[3]用变分模态分解(variational modal decomposition,VMD)和谱峭度的方法对轴承早期故障进行诊断,并与直接包络和经验模态分解(empirical mode decomposition,EMD)包络比较,发现该方法优于其他两种。陈志刚等[4]为提高早期滚动轴承噪声信号的鲁棒性,用峭度对信号进行重构降噪并提取瞬态特征,实验发现该方法的抗噪性较好。王志坚等[5]选取MED作为总体平均经验模态分解(ensemble empirical mode decomposition,EEMD)的滤波器,通过循环自相关解调分析发现,该方法可突出轴承在强背景噪声情况下的微弱故障特征。齐咏生等[6]针对滚动轴承信号非平稳性和非线性等特点提出了自适应信号稀疏共振分解(adaptive resonance-based signal sparse decomposition,ARSSD)和多点峭度最优最小熵解卷积修正的(multipoint kurtosis optimal minimum entropy deconvolution adjusted,MK-OMEDA)的方法,从多点峭度谱图中可清晰发现复合故障脉冲频率。胡爱军等[7]将谱峭度(spectral kurtosis,SK)和最大相关峭度解卷积(maximum correlate kurtosis deconvolution,MCKD)相结合诊断轴承复合故障,实验发现SK和MCKD相结合可发挥各自的优势,实现方便,具有一定的实际应用价值。姚成玉等[8]用MED对信号解卷积,将解卷积后的信号进行VMD,并用扩展粒子群算法和支持向量机识别并分类故障特征,实验发现该方法识别效果和准确率较高。综上所述,解卷积可增强信号脉冲冲击,提高信噪比,且易于实现。
课题组提出利用基于最小熵解卷积(minimum entropy deconvolution,MED)和加权多尺度字典学习(weighted multi-scale dictionary learning,WMSDL)的方法对滚动轴承内圈故障进行诊断。课题组采用MED算法对采集的信号进行解卷积降噪,用WMSDL的方法为降噪后的信号提取稀疏字典,进一步提高信号信噪比,最后进行包络解调获取故障特征频率。通过分析仿真信号和实际轴承信号数据验证所述方法的有效性。
1 基本理论
1.1 最小熵解卷积
最小熵解卷积最早是由Wiggins提出。MED本质上是信号的还原过程。MED的方法是设计一个逆滤波器与采集信号卷积,目的是使故障特征熵值最小、峭度(kurtosis)最大。由于峭度能很好的反应故障脉冲成分,因此该方法非常适用于冲击性故障的降噪和滤波[9]。
假设发生故障时的振动信号是由多个分量组成:
y(n)=h(n)*[x(n)+e(n)]。
(1)
式中:y(n)为采集的振动信号,h(n)为系统单位脉冲序列响应,x(n)为脉冲序列,e(n)为系统噪声。
由于滚动轴承脉冲序列x(n)受系统噪声和传递路径的影响使得采集到的振动信号y(n)失去原有特征。通过逆滤波器f(n)与采集的信号y(n)卷积,使其恢复原有特征,即
(2)
式中,H为滤波器长度。
Wiggins假设使得峭度最大的逆滤波器f(n)优化目标为[10]:
(3)
式中:N为采集信号的数据长度,k为峭度。
通过对优化目标求导为零,求解最优逆滤波器。求解结果为:
(4)
式中:采集的振动信号y=[y1y2…yN],脉冲序列x=[x1x2…xN]。
对式(4)进行更新迭代,并用新滤波器计算更新后的输出x(n),利用迭代次数和峰度作为迭代停止条件,从而选择最优的逆滤波器,实现对原始信号的滤波降噪。
1.2 加权多尺度字典学习原理
1.2.1 稀疏表示和字典学习
字典学习是为样本找到一个合适的字典并转化为稀疏表示的形式,简化学习任务,降低模型复杂度,也称稀疏编码。字典学习更倾向于学习字典的过程,稀疏编码则侧重于稀疏表示的过程。两者均在同一优化过程中求解,所以笼统的称为字典学习[11]。
给定数据集X=(x1,x2,x3,…,xm)d×m,则字典学习的简单形式为:
(5)
式中:Dd×ω为字典矩阵,ω为字典的词汇量,稀疏矩阵A=(α1,α2,…,αm)ω×m,αi为xi的稀疏表示。

(6)
其次,以αi的初值来更新字典D:
(7)
式中:稀疏矩阵A=(α1,α2,…,αm)ω×m;‖·‖F为矩阵的Frobenius范数。
令字典矩阵D的第i列为bi,αi为稀疏矩阵A的第i行,则式(7)可写为:
(8)
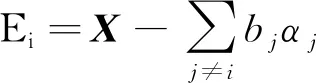
稀疏表示可降低故障特征模型复杂度,简化学习任务,实现瞬态轴承故障信号的重构和故障特征的提取与分离,从而更有效的识别出轴承故障信号。
1.2.2 加权多尺度字典学习WMSDL
加权多尺度字典学习主要是由多尺度变换、信号的系数正则和源区分加权项组成,课题组采用赵志斌等提出的WMSDL模型[12],则有:
(9)
(10)
式中:Γi表示将信号xn×1的第i个数据点开始以C为长度转化为CN×M,WT表示前向多尺度变换,Dl表示字典第l层,Al是系数第l层,K是对角矩阵包含故障信息的峰度,且有:
(11)
其中:s为总分解水平;权重kl的峰度为:
(12)
式中:〈·〉表示平均值,rl表示信号第l个分解的系数重构。
在WMSDL模型中,DA为鉴别学习,WTy为稀疏表示,λP(A)为正则项。WMSDL模型的特点:①将轴承故障信号分解成不同的尺度,每个尺度会有一个子字典,这使得组合字典D具有多尺度特性;②由于子字典是从不同频带中分解学习得到的,所以可有效的保障故障特征的周期性和全局性;③故障信号的数据长度N可人为设定,减少了计算的复杂度;④加权矩阵K对谐波干扰有很好的滤波作用。
2 仿真分析
为验证该方法的有效性,课题组模拟滚动轴承在强噪声的环境下内圈故障所产生的振动冲击信号,并向信号中添加较强高斯白噪声,仿真信号[13-16]:
(13)
式中:s(t)为脉冲冲击成分,幅值A0为1,调制频率fr1和fr2分别为50和90 Hz;载波频率fn为280 Hz,采样频率fs为8 kHz,采样数n为20 000;δ(t)为高斯白噪声。
图1(a)所示为仿真内圈故障信号的时域波形,图中可以看到由于信号中存在较强的高斯白噪声,仿真信号的故障冲击成分被噪声所淹没,因此在信号包络谱图1(b)中显示在频率小于100 Hz的噪声较为明显,在频率大于100 Hz较弱的故障特征频率被较强的噪声所淹没。图2所示为经MED算法对仿真信号进行还原后的脉冲冲击,其滤波器长度为100,算法迭代终止数为100,迭代终止条件为迭代过程中的峰度变化低于阈值迭代终止,该阈值设为0.01。图2(a)与图1(a)相比,仿真信号中的故障脉冲成分明显增多。对解卷积后的信号利用加权多尺度字典学习稀疏分解后再进行平方包络解调,结果如图2(b)所示。从图2(b)中可明显观察出调制频率fr1和fr2的二倍频和其他冲击成分处谱线幅值,轴承内圈故障特征频率被准确清晰地提取。
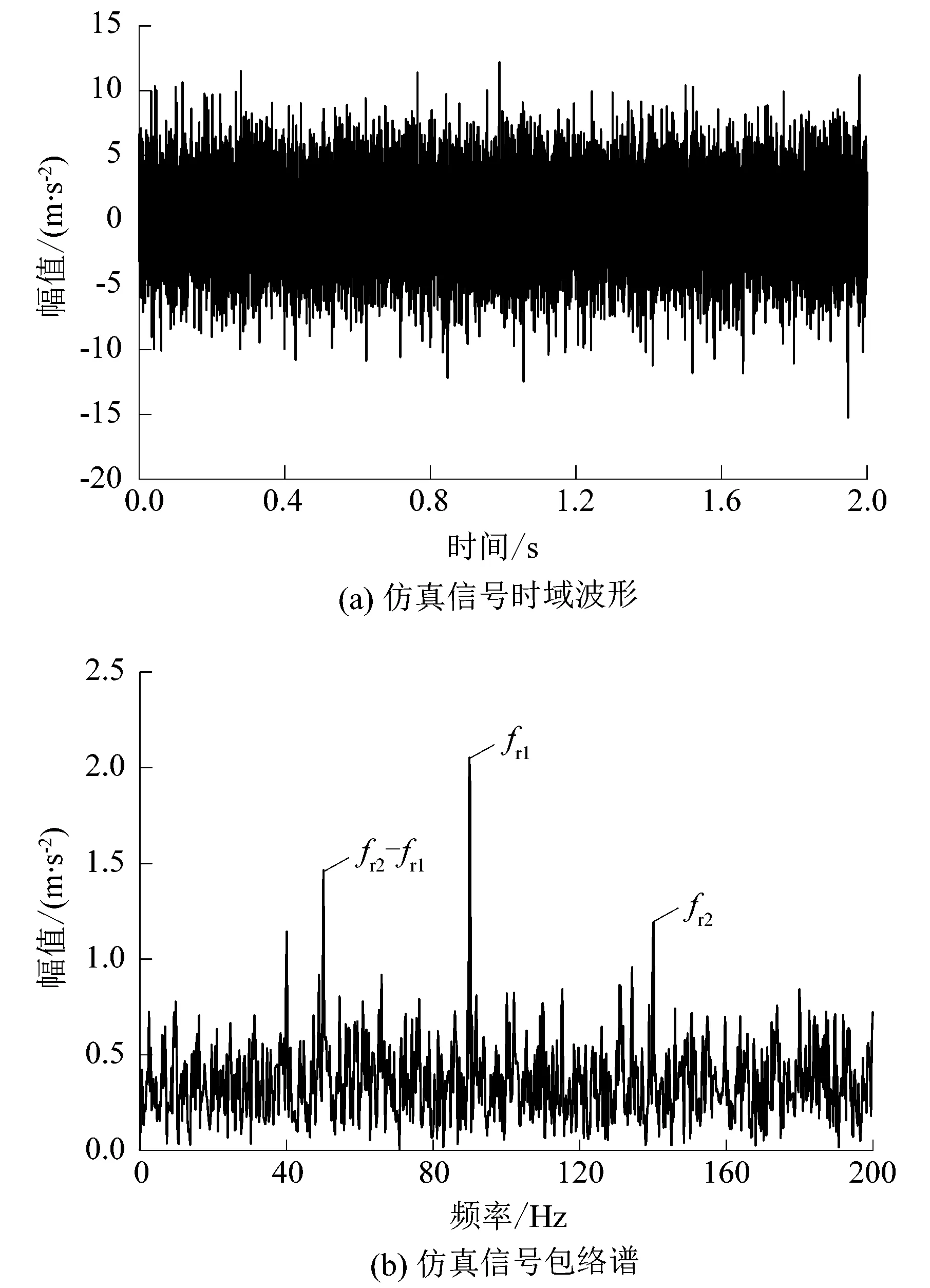
图1 仿真信号时域波形及包络谱

图2 仿真信号MED后时域波形及仿真信号经MED和WMSDL后包络谱
3 实例分析
为验证该课题组提出方法的可行性,采用雷亚国课题组的滚动轴承加速寿命实验数据集进行分析[17]。
轴承加速寿命测试平台电机转速为2 250 r/min。课题组采用2个单向加速度传感器PCB 352C33获取轴承全寿命周期振动信号并分别测试轴承的水平和竖直方位,采用DT9837采集振动信号。轴承加速寿命实验台如图3所示。滚动轴承选用LDK UER204,采样频率为25.6 kHz,施加的径向力为11 kN,轴承相关参数如表1所示。

图3 轴承加速寿命实验台

表1 轴承内圈基本参数
课题组选取测试轴承内圈数据集Bearing 2_1,其中样本总数为491,额定寿命为6.786~11.726 h,实际寿命为8.183 h,为方便分析选取2组垂直振动信号数据样本序号80和216进行分析。采用MED对输入信号进行降噪,然后利用WMSDL对降噪后的信号进行包络解调,算法涉及的参数如表2所示。

表2 算法参数设置
图4所示为滚动轴承内圈振动加速度时域波形图,由于受噪声以及谐波干扰,对信号直接做包络解调无法准确识别故障特征频率。从表2所设置的参数可看出输入信号经MED解卷积后,信号相较于原始信号中低频噪声成分减少许多,信号的信噪比提高,脉冲冲击成分较输入信号有所提升,而这些冲击成分则为轴承内圈故障特征信息,如图5所示。从解卷积后信号的冲击周期可看出,冲击按振幅大小可分为大周期和小周期2种。其中,大周期类似于样本序号216中0.9 s处,小周期类似于0.1 s处,信号的信噪比明显提高。
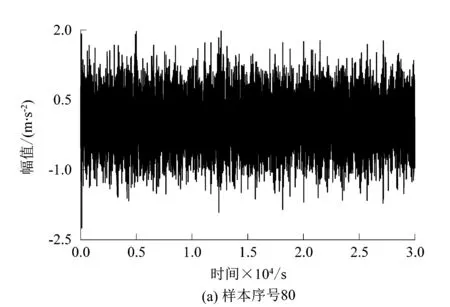
图4 样本数据原始信号加速度时时域波形
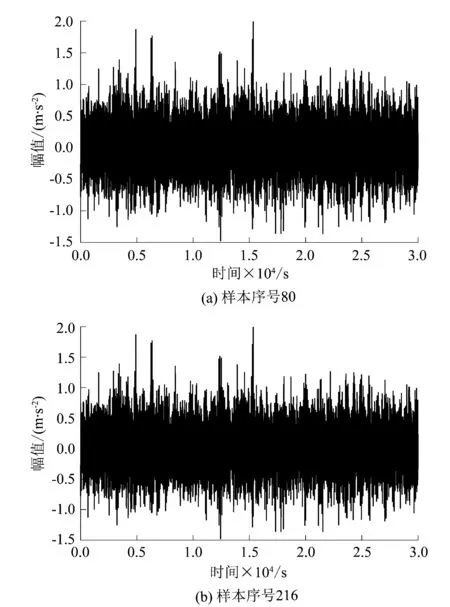
图5 样本信号经MED滤波后的时域波形
图6所示为信号经MED解卷积滤波后使用WMSDL再平方包络解调的谱图,可发现同一滚动轴承在同样的工况下均在其转频及其倍频处出现较强的频率尖峰,因此可判断出滚动轴承内圈存在局部损伤,分析结果与预先设置的故障特征情况一致。
由上述的方法对滚动轴承故障特征进行分析可知,MED和WMSDL相结合能很好的突出滚动轴承故障特征频率,同时也能提高信号的信噪比,从而准确的诊断出滚动轴承的故障。
4 结语
课题组基于滚动轴承内圈故障特征频率存在环境噪声干扰等状况,提出最小熵解卷积算法结合加权多尺度字典学习的方法进行降噪和稀疏表示,再进行包络解调提取轴承内圈故障特征频率。轴承内圈故障特征在故障初期非常微弱,对提出的模型通过仿真信号和实例验证发现,课题组提出的方法可有效降低滚动轴承摩擦故障特征信号中的噪声,增强微弱故障冲击成分,便于对故障特征早期诊断,具有一定的实际工程意义。

