基于DTCWPT分频特征和BiLSTM的滚动轴承剩余寿命预测

魏 豪， 权 伟， 何建国， 张 玮

(西安工程大学 机电工程学院, 陕西 西安 710048)

滚动轴承作为旋转机械核心零部件，广泛应用于机械设备中，对机械设备的安全运行发挥着至关重要的作用。滚动轴承的状态识别和寿命预测也是现在众多学者关注的热点问题[1-2]。轴承服役期间逐渐产生的退化和损伤，若未能及时发现或提前预测，可能会导致严重的安全事故和经济损失。因此，有必要对滚动轴承的可靠性进行评估，预测其剩余使用寿命，以维持旋转机械安全可靠运行。

目前，滚动轴承剩余寿命预测方法主要分为基于物理模型的方法和基于数据驱动的方法[3]，其中数据驱动方法更加符合现代化复杂工业和工业大数据环境，故基于统计分析和人工智能等数据驱动方法被广泛应用于寿命预测领域[4-5]。

基于数据驱动的轴承剩余使用寿命预测核心步骤为退化特征提取[6]，因此近年来国内外学者针对轴承的退化特征提取问题开展了大量研究，如经典时域、频域统计特征[7]，经验模态分解[8]，小波包分解[9]等时频域特征，机器学习[10]、深度学习[11]等退化特征提取方法被相继应用于寿命预测领域。其中，结合经典统计特征的改进特征趋势因具有较强可解释性受到众多学者青睐。曾大懿等[12]提出一种基于退化特征间相关性的评价指标，将其应用于统计特征和深度学习特征进行预测，并取得优良效果。李卓漫等[13]提出基于卷积自编码器和混合灰狼优化支持向量回归机的性能退化趋势预测方法，利用卷积自编码器将高维经典统计指标进行降维，取得了优化特征趋势的效果。陈昌等[14]提出使用威布尔形状分布参数作为轴承退化特征，结合粒子群优化的最小二乘支持向量机得到了准确的预测效果。上述退化特征提取方法虽具有一定效果，但是并未考虑到轴承初期故障包含于噪声之中，会导致退化特征状态识别滞后于真实轴承状态。

故课题组提出一种基于快速谱峭度与DTCWPT结合BiLSTM的滚动轴承剩余寿命预测方法：利用快速谱峭度对信号中冲击的敏感性，结合双树复小波包故障中心分频带提取退化特征有效降低信号噪声干扰成分；通过增强特征趋势提高对轴承真实状态的刻画能力，使用BiLSTM进行寿命预测；最后进行了试验数据验证，并与LSTM预测方法进行比较。

1 算法原理

1.1 快速谱峭度原理

快速谱峭度方法是由Antoni[15]在带通滤波的基础上提出的，其定义为：

Kx(f)=[S4(f)/(S2(f))2]-2。

(1)

式中：f≠0,Sn(f)为信号的n阶谱矩，且Sn(f)=E〈|L(f,t)|n〉,其中E〈·〉为取均值,|·|为取模，L(f,t)是信号xt在f处的复包络。

以二叉树滤波器组为例，算法的步骤如下：

1) 构造一个截止频率fc=1/8+ε的低通滤波器h(t)，ε>0。以fc=0.4为例，h(n)构造通频带为[0,1/4]的准低通滤波器h0(n)和通带为[1/4,1/2]的准高通滤波器h1(n)，具体如下：

(2)

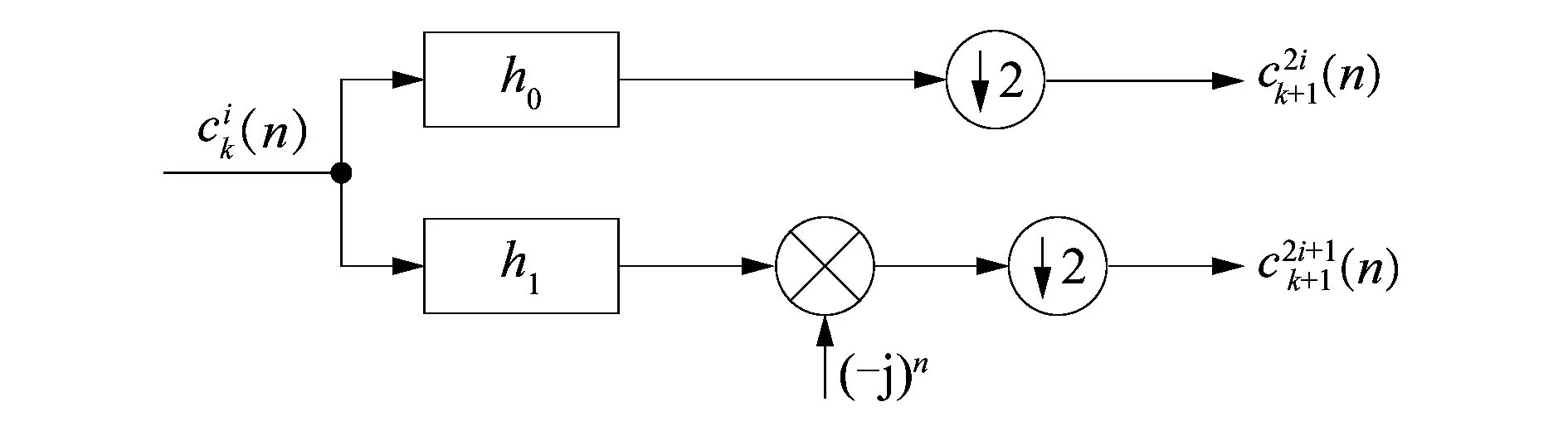
图1 低通/高通分解

图2 二叉树滤波器组及相应的滤波结果

3) 对于每一个滤波器结果，按照峭度公式计算其谱峭度：

(3)

式中，c是滤波信号的幅值。

4) 将所有的谱峭度汇总，从而得到“谱峭度图”。峭度值大的频带预示着该频带为冲击信号激发的共振频带。

1.2 双树复小波包

双树复小波包可以视为由2个并行的离散小波包变换组成，2个并行的离散小波包分别为双树复小波包的实部树和虚部树。为了有效保留信号中所有信息，解决原始小波包中信息丢失的问题，课题组重构和分解信号使其始终保持虚部树位于实部树的中间位置。DTCWPT具有近似平移不变性这样的优良性能，对信号分频处理具有更加良好的效果。

复小波基函数构造如下：

Ψc(t)=Ψr(t)+jΨi(t)。

(4)

式中：Ψr(t)为实部，Ψi(t)为虚部，如果Ψr(t)和Ψi(t)构成一对希尔伯特变换对，则Ψc(t)为解析信号。

复尺度函数与复小波函数的构造方法相似。DTCWPT实部变换的小波系数dl(k)和尺度系数εJ公式为：

(5)

(6)

式中：l为尺度因子，J为分解层数，Ψh(t)为实部树的小波函数，Φh(t)为实部树的尺度函数。

1.3 特征提取及特征筛选

经双树复小波包分频降噪处理后，对故障中心频带重构信号进行经典时域、频域特征提取。提取到的时域特征有：均方根值、最大值、最小值、峰峰值、绝对平均值、波形指标、峰值、峰值因子、脉冲因子、平均值、峭度、峭度因子、方根幅值、裕度因子、裕度指标、余隙因子、基尼系数和中值因子。提取到的频域指标有： 频域均值、频域均方根和频域重心。

为了获得对剩余寿命预测获得更有效和高效的退化特征，选用2个退化特征评估指标——时间相关性和鲁棒性。时间相关性度量用于评估滚动轴承性能的退化特征与轴承运行时间的相关性；鲁棒性度量用于评估特征指标刻画轴承性能退化趋势的鲁棒性。评估参数公式如下：

(7)

(8)

式中：corr (F,T)为时间相关性，F为特征序列，T为时间序列，rob (F)为鲁棒性，tl表示第l组特征对应的时间标签，f(l)表示l组特征，fP(l)表示平稳部分，fR(l)表示随机余量，L为样本时间总长度。

2 剩余寿命预测

2.1 BiLSTM原理

在长短记忆人工网络(long short-term memory, LSTM)解决循环神经网络(recurrent neural network， RNN)处理时间序列梯度消失和梯度爆炸问题的基础上，研究人员针对LSTM无法处理后向信息导致预测结果不准确问题，提出了BiLSTM通过前向和后向信息神经网络获取预测结果，提升了预测准确性。BiLSTM结构如图3所示。

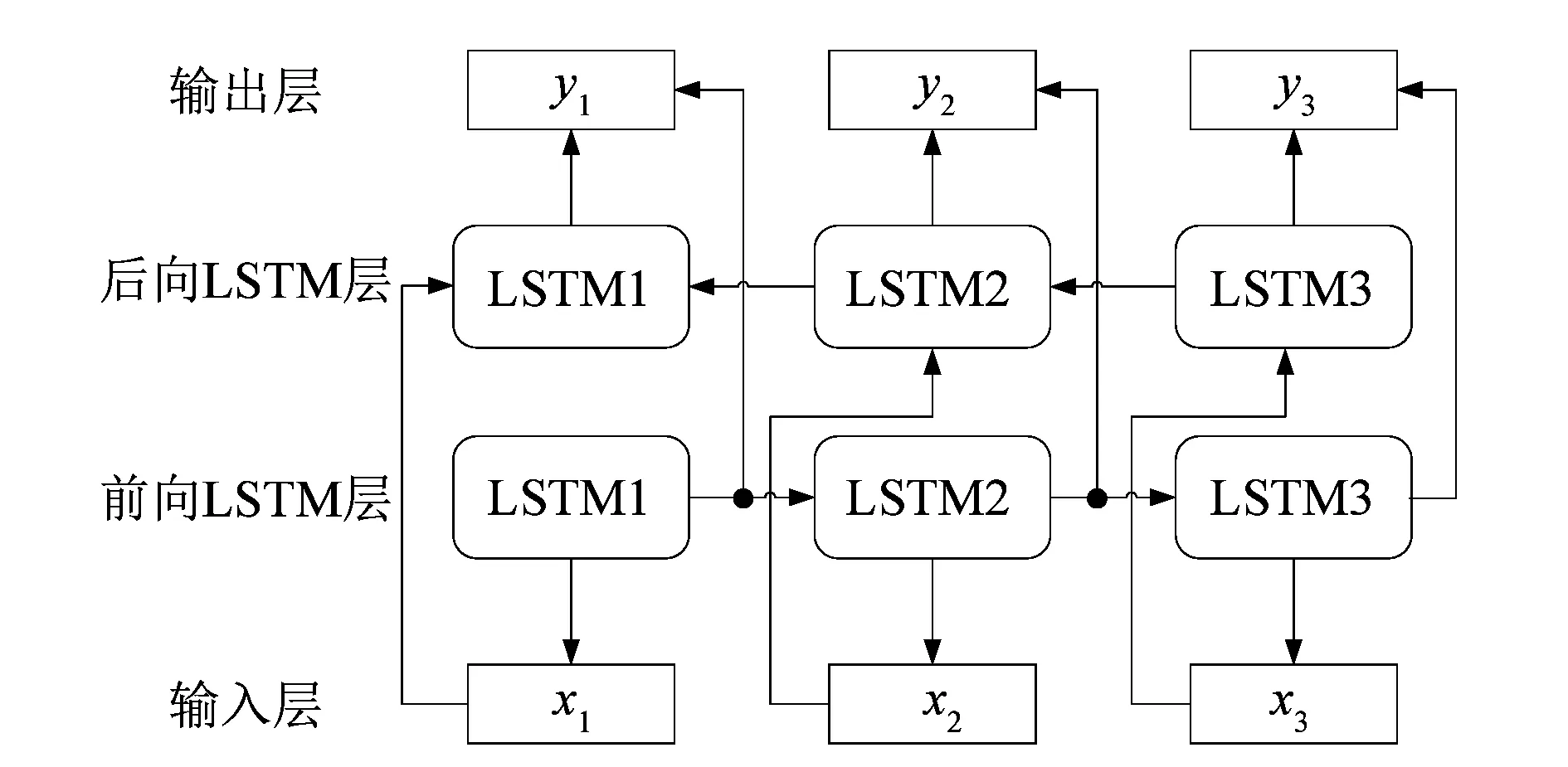
图3 BiLSTM网络结构

由图3可以看出，BiLSTM处理时间序列时，前向和后向的独立隐藏层可以同时捕获之前和之后的信息，针对轴承全寿命数据的长时间序列，具有更加优良的预测性能。

2.2 寿命预测流程

寿命预测流程如图4所示，具体步骤如下：

图4 寿命预测流程图

1) 获取轴承退化振动加速度信号；

2) 使用3σ准则估计轴承故障起始时间；

3) 对预测起始时间后的振动数据进行快速谱峭度计算，确定滤波中心频带；

4) 对振动信号进行双树复小波包分频处理；

5) 选取包含故障中心频率的频带重构信号提取时域、频域特征；

6) 使用时间相关性、鲁棒性指标对特征进行筛选；

7) 将筛选特征输入BiLSTM模型训练并预测。

3 试验分析

3.1 数据准备

为验证所提出方法的有效性，开展轴承全寿命试验获取轴承全寿命数据，试验针对SKF 6312/C3深沟球轴承开展，表1所示为SKF 6312/C3深沟球轴承参数。试验台共安装4套轴承，使用加速度传感器监测振动信号，使用电流钳监测电流信号，使用键相传感器监测主轴转速。

表1 SKF 6312/C3深沟球轴承参数

试验每间隔1 min采集1.28 s数据，采样频率12 800 Hz，包含4套轴承的振动、电流和转速等信号，试验工况如表2所示。

表2 试验工况

试验台与测点位置如图5所示。

图5 轴承寿命试验台及测点

试验所使用的4套轴承实际额定寿命、全生命周期运行时长及各轴承运行至寿命终止的失效形式如表3所示。

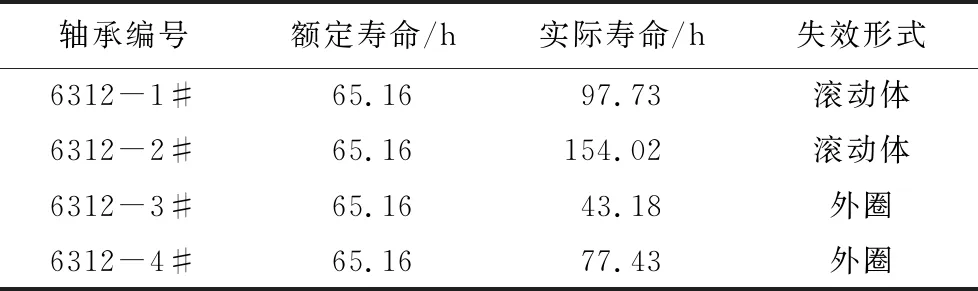
表3 试验轴承寿命及失效形式

得到轴承全寿命试验数据，首先使用3σ准则估计故障发生时刻，并对故障发生时刻振动信号进行快速谱峭度计算，结果如图6所示。快速谱峭度图中的颜色深、浅代表信号所在频带的峭度值大、小，颜色越深，峭度值越大，颜色越浅，峭度值越小；而峭度值大的频带预示着该频带为冲击信号激发的共振频带。可以看出当信号在4.4 kHz频带时，峭度值最大，故障冲击成分包含最多。

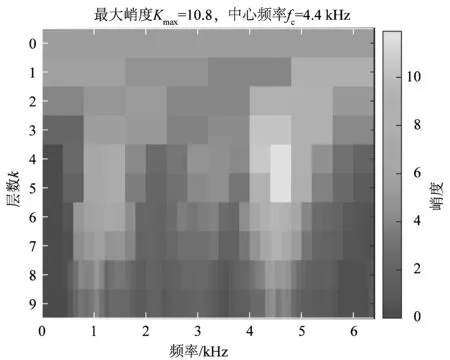
图6 快速谱峭度图

对故障发生时刻原始振动信号和包含故障中心频率4.4 kHz分频带重构时域信号进行包络解调精密分析，结果如图7所示。由图7可见：总频信号中因包含大量噪声，导致故障特征无法识别，但分频包络谱中包含清晰的故障特征，证明通过DTCWPT对故障滤波中心频带滤波后，可有效减少信号中的噪声干扰，所提取分频退化特征更加准确地反映轴承真实状态。

图7 总频与分频信号包络分析

然后对特征进行筛选，使用轴承6312-4#数据，分别从21维特征中筛选出时域统计量绝对平均值和方根幅值及频域统计量频域均值3个特征指标作为寿命预测模型训练数据集，具体内容如图8所示。

图8 特征筛选

传统轴承剩余使用寿命(remaining useful life， RUL)将轴承退化指标和时间构造为一个线性函数，但真实轴承退化一般发生在轴承全寿命的后期，前期健康阶段的退化可以忽略不计。为了更好的模拟轴承剩余使用寿命与时间的关系，构造分段线性RUL目标函数,具体如图9所示，将3σ准则估计的故障起始时刻之前看做健康阶段，之后看做轴承退化阶段，进行分段线性函数模拟。

图9 轴承分段线性RUL曲线

3.2 BiLSTM模型预测

为验证BiLSTM预测模型配合分段线性RUL函数对长时序列的预测性能，现将6312-1#数据归一化特征作为训练集对模型进行训练，并使用训练好的模型分别对测试集轴承6312-2#，6312-3#和6312-4#进行预测，训练模型参数如表4所示，图10所示为滚动轴承RUL预测结果。

表4 网络模型参数

图10 BiLSTM模型剩余使用寿命预测

使用相同训练集和测试集数据验证LSTM预测模型效果，为保证对比公平性，模型参数与BiLSTM一致，LSTM预测结果如图11所示。

对比图10和图11发现，采用课题组提出方法提取的轴承退化特征结合BiLSTM预测模型的预测结果与真实值拟合度更高，并且根据所构造的分段线性RUL函数可以有效提升轴承末期退化阶段预测准确率，与轴承寿命预测所关注的重点一致，进一步证明了本文方法的实用性。模型均方根误差如表5所示，可以看出，BiLSTM预测模型的均方根误差(root mean square error， RMSE)均远小于LSTM预测模型，验证了BiLSTM结合本文分段线性RUL函数对长时和短时轴承寿命预测的通用性。

图11 LSTM模型剩余使用寿命预测

表5 模型均方根误差对比

4 结论

针对轴承传统退化特征导致预测精度差的问题，课题组提出了基于分频特征结合BiLSTM的轴承剩余使用寿命预测方法，经过试验验证，所得结论如下：

1) 通过快速谱峭度和DTCWPT方法提取的分频退化特征可以有效降低信号中的噪声成分，准确刻画轴承的真实退化状态。

2) 结合分段线性RUL函数的BiLSTM预测模型，可以准确预测长时序列，并准确预测轴承全寿命末期结果，符合轴承寿命预测的实际需求；对比LSTM预测模型，切实提升了轴承剩余寿命预测的准确性。