基于混合蚁群算法的货物码垛模型研究
侯克金, 袁锐波*, 杨灏泉, 李 焕
(1.昆明理工大学 机电工程学院, 云南 昆明 650500; 2.云南柔控科技有限公司, 云南 昆明 650031)
目前,我国制造业正处于基本实现数字化网络化的上升期,企业正是数字化转型与改造的主体,仓储物流的高效管理是建设智能共享工厂中重要的一步,而自动化物流系统中需要解决的关键性难题就有货物的在线码垛问题[1]。货物在线码垛问题本质上为三维装箱问题(three-dimensional bin packing problem,3D-BPP),是一种复杂的空间组合优化问题,在理论上属于NP完全问题[2]。
三维装箱由于其广泛的应用领域,国内外学者对其进行了大量深入的研究,主要研究方向为模型的构建以及现代智能算法的优化。在模型构建方面,大多学者采用启发式的算法。F.G.Ortman等[3]主要是利用启发式、人工智能等方法将装箱问题的布局进行优化;阎威武等[4]是采用启发式算法来解决实际问题,采用了空间的分割与合并的策略,并且考虑了货物的装载方向、重量和卸载位置等约束,选取最优装载方案;张德富等[5]提出了一种有效的复合块生成算法和多层块选择算法来搜索最合适的块进行装载,在填充率上较以往三维装箱问题有所提高;吴蓓等[6]在空间搜索策略方面提出了自适应随机重力式空间搜索算法。在智能算法优化方面:朱向等[7]设计了双层混合遗传算法对最优方案进行求解;李伟等[8]将禁忌搜索算法和遗传算法相结合来解决集装箱的装载问题;张长勇等[9]提出了拟人装载策略,重点考虑了货物装载顺序以及垛型稳定性约束,并且改进了标准的遗传算法,加入适应度变换、最优保存策略;文献[10]中张长勇等基于关键点策略,以改进的粒子群算法进行空间位置的最优解的搜索,空间利用率有了显著提升。对于本文中研究涉及的在线装箱问题:2007 年Gerhard等[11]根据货物信息是否已知以及货物码放是否按照一定顺序,将装箱问题分为离线装箱与在线装箱;尚正阳等[12]将三维问题转化为有高度约束的二维问题,在大规模或者需要在线快速装箱时有较高的适应性,但面对强异构型货物时有一定的局限性;文献[13]中张长勇等对在线装箱问题提出了一种极值点寻找所有装箱位置点与模糊算法搜索最佳装箱点的融合算法,容积率达到一个较高的水平。
早期学者大多专注于离线式装箱的研究,后续随着装箱要求的不断提高,需要实时在线装箱,但目前对于在线式的多规格货物的装箱研究仍然较少。课题组针对实际托盘码垛作业,首先建立了码垛问题的数学模型,提出了实时在线的码放策略,同时采用混合蚁群算法来优化货物的码放位置与姿态,提高了托盘的空间利用率以及码垛的效率。通过建模与仿真,证明了课题组的研究可以预估货物的垛型,这也为以后机器人自动化码垛提供了参考。
1 模型建立
1.1 问题描述
托盘码垛即工业机器人将货物放置到托盘上,此时物件是由传送带实时传送到机器人附近,所以托盘码垛问题可以视为在线装箱问题,要求装载算法能够做到对货物进行实时规划布局。
目前大多数码垛为同种类货物的码垛,为简化问题,针对多规格货物的码垛做以下假设和规定:①货物简化为质量均匀的长方体且为刚体, 忽略挤压变形;②货物的重心在其几何重心上;③任何2个货物之间不能重叠;④根据实际货物情况,规定货物可以悬空的底面积;⑤为保证货物的稳定性,整体垛型的重心需在安全范围之内。
1.2 数学模型
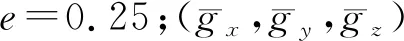
(1)
(2)
xi≥xj+lj∨xi+li≤xj。
(3)
yi≥yj+wj∨yi+wi≤yj。
(4)
zi≥zj+hj∨zi+hi≤zj。
(5)
(xj+lj)/(xi+li)≤1+e。
(6)
(yj+wj)/(yi+wi)≤1+e。
(7)
zi+hi=zj。
(8)
(9)
T=∑liwihi/[max (xi+li)max (yi+wi)max (zi+hi)]。
(10)
式中,∀(i,j)∈{1,2,3,…,n}。
式(1)表示货物不超过托盘的承载尺寸范围;式(2)表示货物的总质量不超过托盘所能承载的质量;式(3)~(5)表示任意2个货物i,j之间不可以重叠;式(6)~(8)表示在货物i上的货物j可以悬空的范围;式(9)表示货物的整体垛型重心在安全范围内;式(10)为目标函数,模型的优化目标为最大化垛型的空间利用率。
2 码放策略
2.1 可放置点策略
根据Crainic T G等[14]、张莹[15]和Mahvash B等[16]对 “关键点”码放策略的研究,提出了最优放置点的启发式算法。
最优放置点搜索原理:每当1件货物码放后,会覆盖1个原来的最优放置点,另外产生3个可放置点(会出现假可放置点,需设置一定规则去剔除假的可放置点),然后根据装载规则以及下一件货物的尺寸来选择出最优的放置货物的坐标点。
详细步骤如下:
1) 构造用于码垛的o-xyz三维坐标系。
2)装入第1件货物。当托盘上没有货物时,有很多可以放置货物的点,但是此时有1个最佳放置点坐标为(0,0,0),当以此坐标为顶点,放入1件货物后,便覆盖原最优坐标点,产生另外3个可放置的坐标点。
3) 放入第2件货物。第2件货物的最佳放置点,需要根据后续的装箱规则得出,此时覆盖原最优放置点,新产生3个可放置点。
4) 码放第3件货物。此时如图1(d)所示,第3件货物与第1件货物的右面刚好齐平或者超出,此时货物3的右侧可放置点为假点,需要剔除。

图1 可放置点示意图
最优放置点启发式算法是可以很好的契合在线装箱的条件,实时做出码放的决策,并给出最优放置点的坐标。
2.2 可放置点坐标及范围
2.2.1 新增可放置点
货物在满足可以装入的情况下,首先可以确定3个后续的货物可放置点坐标,理论上分别位于货物平
行于x轴、y轴、z轴方向上的边的延长线上; 其次, 可以确定每个可放置点的空间范围。
如图2所示,假设尺寸为(li,wi,hi)的货物i,放在可放置点o处,o点坐标为(ox,oy,oz),则理论上其新增的3个分别与x轴或y轴或z轴同方向上的可放置点坐标计算方式如下:

图2 可放置点坐标及范围
(11)
假设可放置点o点的空间范围为So,在o点处放置1个货物i,则x轴向可放置点的剩余可放置空间为Sx,y轴向可放置点的剩余可放置空间为Sy,z轴向可放置点的剩余可放置空间为Sz,其计算方式如下:
(12)
分别按照剩余空间的算法进行计算剩余空间范围。另外,z轴方向比较特殊,由于可以允许货物部分悬空,因此这里设置悬空因数e,表示可以悬空的长度占底面边长的比例。
2.2.2 确定最优可放置点
考虑到实际机器人作业情况,货物码放的顺序一般为先沿着托盘的一条边,然后铺满底面,货物的高度差不能太大,最后不断码高垛型,因此需要改变放置点的优先权,Px>Py>Pz,使其按照机器人可作业的方式进行。将正要码放的货物在每个放置点试放,并改变不同的摆放姿态,这里设置适应值函数来评价可放置点优劣。
(13)
式中:Fi为货物i在每个可放置点的适应值函数,Fi最小时表示该点为最优放置点;st表示为货物i在左、后、底面的面积,sT为货物i在左、后、底面所接触的其他货物的面积;N(s)表示货物i在左、后、底面所接触到的其他货物数,1≤N(s)≤3。
3 混合蚁群算法
由于托盘码垛的可放置点选择是根据当前货物择优选择的,不能进行整体空间的合理规划,而且后续可放置点较多时,难以挑选出最合适的货物以及最优的放置点,因此设计了混合蚁群算法来得到一个合理的码放顺序以及货物摆放姿态。
3.1 算法描述
根据可放置点寻优的策略,同时借鉴常用的免疫遗传算法求解三维装箱问题的交叉变异的思路,设计混合蚁群算法来求解该问题。因此需要重新定义蚁群算法中的蚂蚁含义、信息素和概率转移函数等特征。
1) 个体信息,将货物视为蚂蚁,蚂蚁数等于货物数。
2) 信息素,蚂蚁搜索的信息素设定为2种,一为货物的选择序列,一为货物的放置姿态。
3) 概率转移函数,即为选择下一件货物的概率,同样设置货物序列选择概率函数和货物姿态选择函数。
4) 目标函数,以货物的体积占用率为目标函数。
3.2 基本定义
对算法的基本初始定义进行设置。
3.2.1 货物的属性
定义货物编号为ki,其中i∈(1,2,3,…,n),表示第i个码放的货物;货物的属性包括两部分:一为定位属性,表示为B={xi,yi,zi,li,wi,hi},(xi,yi,zi)为货物的定位坐标,{li,wi,hi}为其长宽高;二为货物的码放属性,为U={u1,u2,u3,…,un},其中ui包括货物的编号和放置姿态,即ui={ki,ri},ri为放置姿态,有∀i≠j,ki≠kj,即对任意2个不同的货物,其编号不能相同。
3.2.2 货物的放置姿态
每个待装货物i有其放置的姿态,用ri表示。当各个方向上没有约束时,其放置姿态有6种,按与托盘的L,W,H分别平行后得到,如下所示:
li∥L,wi∥W,hi∥H,ri=1;
li∥W,wi∥L,hi∥H,ri=2;
li∥H,wi∥W,hi∥L,ri=3;
li∥H,wi∥L,hi∥W,ri=4;
li∥W,wi∥H,hi∥L,ri=5;
li∥L,wi∥H,hi∥W,ri=6。
如果有方向约束,则从其中选出所对应的ri,放置姿态示意如图3所示。
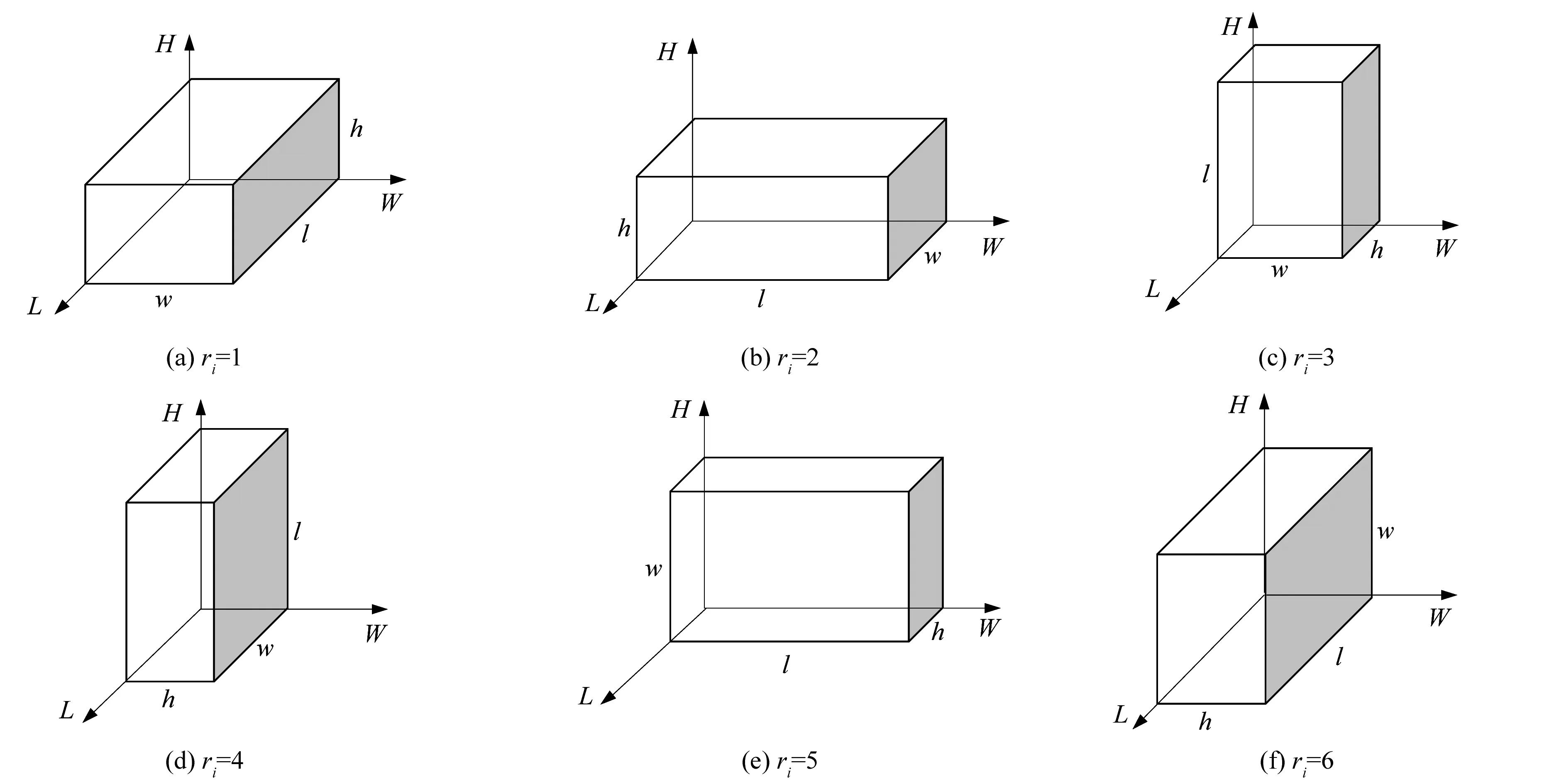
图3 货物摆放姿态示意图
3.2.3 信息素函数
(14)
式中,τi,j(0)为初始时刻货物i到货物j的信息素。
如果选择不同的货物,则信息素增大,有较大的趋势选择另一种货物,避免出现选到同一个货物的情况。
为保证货物可以顺利的放进箱体中,首先对每个货物进行姿态分析,即筛选出可以放进箱体中的姿态形式。具体方法为:将货物做6种姿态摆放,判断其是否可以放入箱体中,然后去除不可以摆放的姿态。

(15)

3.2.4 货物选择概率函数
蚂蚁搜索路径上的信息素以及根据概率转移公式,通过轮盘赌法选择下一个要码放的货物。
t时刻,蚂蚁m在货物i码放完成后选择货物j的概率转移函数为:
(16)

(17)
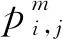
从概率转移公式可以看出,货物选择下一个货物的概率与货物选择的信息素成正比,因此只要经过迭代后,在最优的路径上留下最多的信息素,那么最后则可以得到最优的货物码放的序列。
3.2.5 姿态选择概率函数
每种货物不同的姿态也影响最终的垛型,因此对于不同姿态的选择也设置了概率函数。
(18)
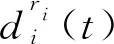
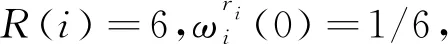
3.3 交叉变异
为了寻找出更优的解,将当代蚂蚁搜索得到的解和历史最优解进行交叉变异,从而形成3个解,然后从3个解中取出最优的装载序列作为本代最优的解。为了使交叉变异后得到的其他2个装载序列是有效的,则需要使同一个货物编号不能在装载序列中同时出现2次。
具体交叉变异操作如下:

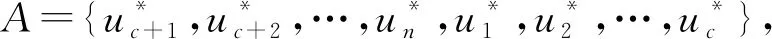
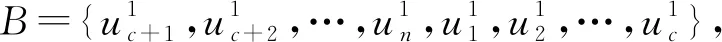
3.4 信息素更新
信息素的更新使最终结果更加偏向于最优值。在计算出蚂蚁的路径(码垛顺序)以及每个箱子的放置姿态后,评选出此时路径中最优的一个目标结果。如果当代最好结果比历史最优值大,则选择该最优值为新的最优值,更新货物选择信息素和货物姿态信息素。分别为2种信息素设置了2个挥发系数,避免某些路径产生局部最优。同时加入负反馈更新,即在一条蚂蚁路径不通时,减少该条路径上的货物选择信息素和姿态选择信息素,加快算法收敛速度。

1) 首先,进行首选货物的信息素更新。
(19)
式中:ρ为货物选择信息素挥发系数,Q为货物选择新增的信息素。
2) 后续货物选择信息素更新。
(20)

3) 货物姿态信息素更新。
(21)
式中:ρ′为货物姿态信息素挥发系数,Q′货物姿态新增的信息素。
同理,若本代同一种货物的摆放姿态和上一代的相同,则使用较小的挥发系数,同时,额外增加下一代相同货物相同的姿态的信息素,保证较大概率选取最优解的货物姿态。
3.5 算法流程
求解该问题的混合蚁群的算法流程如下:
1) 首先获取货物信息。
2) 初始化蚁群个数m、迭代次数iiter、货物选择信息素和货物姿态信息素以及它们各自对应的挥发系数。
3) 选出初始码放货物,然后根据概率选择公式,选择下一件货物以及其放置姿态。
4) 判断是否有剩余箱子,若是,对货物选择和姿态信息素进行负反馈,跳转到步骤3);否则,跳转到步骤5)。
5) 在得出一代所有的货物码放序列后,选出最优的货物码垛序列。
6) 判断是否为历史最优码垛顺序,若不是,则最优值不变,跳转到步骤7)更新信息素;否则,更新最优值。
7) 更新货物姿态和货物选择信息素。
8) 判断是否大于最大迭代次数,若是,则循环结束;否则,返回步骤3)。
9) 输出最优码放序列。

图4 混合蚁群算法流程图
4 实例测试分析
为验证混合蚁群算法对于托盘码垛问题的适用性,实验数据采用云南某公司在实际托盘作业中的货物订单信息。因为其一般托盘码放的货物数量在 24~30件之间,因此,分别选取数量为25和30的货物订单作测试,25和35件特码放货物数据如表1和2所示。托盘的尺寸为1 300 mm×1 000 mm,限高1 900 mm,允许承载的质量为800 kg。

表1 25件待码放货物数据
实验仿真环境为:CPU为i5-6200U;主频为2.4 GHz;内存为8 GB;操作系统64位Windows10;编程环境为Python3.8及Visual Studio Code1.59。实验针对不同数量的货物选择等量的蚂蚁数,每个蚂蚁分别代表每一种货物,最大迭代次数iiter为100,货物选择信息素挥发系数ρ=0.15,货物选择新增的信息素Q=0.30,姿态信息素挥发系数ρ′=0.10,姿态新增的信息素Q′=0.16,每种数量的货物分别测试5次。
分别运用可放置点算法和混合蚁群算法进行实例测试,测试的结果见表3,货物码垛仿真效果图见图5。从仿真图中可以很明显地看出混合蚁群算法所仿真出的垛型,货物排列紧密,平整性较高,没有较大空隙。

图5 多规格货物码垛仿真图
由表3数据可知:可放置点的算法在码垛高度上均高于优化后的混合蚁群算法的垛型高度;混合蚁群算法可以明显提高托盘码垛的空间利用率,可放置点的算法空间利用率在76.45%,优化后平均空间利用率在85.46%,平均提高了9.11%;在算法求解时间上,混合蚁群算法相较于可放置点算法较长,因为混合蚁群算法为了寻找出合适可放置点和货物而进行了迭代,增加了算法运行的时间,但时间在实际作业要求内,可以作为参考。

表2 30件待码放货物数据

表3 多规格货物码垛测试数据
由表3和图5可知:多规格货物的码垛,可放置点算法可以在较短的时间内仿真出货物的垛型,但是空间利用率方面有待提高;混合蚁群算法优化后,可以使空间利用率提升9.11%,但是算法的求解时间相较于可放置点算法较高,对于在线式的装箱有一定的影响,但在码垛的可控制范围内,因此混合蚁群算法仍具有较高的适应性。
5 结语
课题组综合考虑了在线码垛作业过程中的实际约束,提出了可放置点的装载策略,并设置了适应度函数来选出当前最优的可放置点。为寻找更合理的码放方案,加入混合蚁群算法进行优化,重新定义信息素以及概率转移函数以解决该问题。最后实例测试表明,可放置点的算法求解时间较短,但是最终垛型的空间利用率不高,混合蚁群算法优化后,码垛的空间利用率提升了9.11%,但求解时间相对延长,从最终目标看,混合蚁群算法模型仍具有一定的可行性,能够增加垛型的空间利用率,减少包装成本,对在线式货物码垛有一定的参考性。
未来进一步研究可以从以下几个方面入手:设定合理的算法中的参数,加快算法收敛速度,减少算法运行时间;考虑机械臂的运动轨迹,使货物的码放顺序更符合实际作业情况。

