基于加速度频域积分的振动位移测量系统
林 培, 许杨剑, 陈栋栋, 鞠晓喆, 梁利华*
(1.浙江工业大学 机械工程学院, 浙江 杭州 310014; 2.浙江省特种设备科学研究院, 浙江 杭州 310020)
在许多场合下需要对结构的振动位移进行测量,例如设备动态特性的研究、地震学科的研究以及桥梁建筑的振动研究[1-2]。杨春[3]利用激光传感器实现了对船舶结构的振动测量。王荣林等[4]利用激光传感器和LabVIEW虚拟仪器平台开发了振动位移测量系统。朱坚民等[5]利用激光测振仪对铣床铣刀的振动位移进行测量。李红伟等[6]利用2个对称放置的电涡流传感器,采用差动相反的思想对磁悬浮转子的轴向位移进行测量。孙志敬等[7]利用电涡流传感器对压缩机的振动进行监测。激光位移传感器具有测量精度高的优点,但激光传感器对安装位置要求较高且测试所得位移信号容易失真。电涡流传感器对被测对象的材料、表面状态都比较敏感,同时电涡流传感器的安装要求也比较高。
加速度传感器具有体积小、质量小和频率范围宽等优点,是工程应用中常用的振动测量传感器之一。由于加速度与位移之间具有积分运算关系,因此可以通过对测量的加速度信号进行积分运算求取位移信号。Arias-Lara等[8]对不同加速度积分方法进行研究,通过实验表明:利用加速度积分求取位移是可行的,积分方法的选取需要根据位移幅值、波形类型等因素来确定。Brandt等[9]研究了加速度频域积分方法以及加权叠加(weighted overlap-add,WOLA)技术的加速度积分方法并与时域积分方法进行比较,通过实验表明:频域加速度积分的精度受数据长度影响,WOLA技术则只适用于稳态情况。李强等[10]将加速度信号转化到频域,并对低频部分清零,在频域对加速度信号进行变换,实现对位移的求取。周小祥等[11]利用加速度时域积分求取位移,针对时域积分容易产生趋势项的问题,利用最小二乘法对趋势项进行消除。但这些研究大多应用于线下求解计算,并未应用于实际工程中的在线测量。
针对上述情况,课题组通过对加速度积分方法进行研究,借助LabVIEW平台和MATLAB开发了基于加速度频域积分的位移测量系统。通过与DIC位移测量方法进行比较,对本系统的测量效果进行了验证。
1 加速度积分方法
动态信号的积分可分为硬件积分和软件积分。硬件积分主要利用积分电路实现,但不适用于测量包含复杂频率成分的信号;软件积分则分为时域和频域积分,主要通过软件算法实现。
1.1 时域积分方法
由于存在各种干扰因素,实际测量得到的加速度信号中会包含直流分量δ,所以加速度信号表达式为:
a=a(t)+δ。
(1)
对加速度信号进行积分得到速度信号:
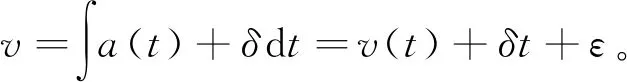
(2)
对速度信号进行积分得到位移信号:
(3)
式中:δ为趋势项中二次项系数,ε为趋势项中一次项系数,e为趋势项中常数项。

1.2 频域积分算法
根据傅里叶变换公式,加速度信号在某一频率ω的傅里叶分量可以表示成:
a(t)=Aejωt。
(4)
式中:a(t)对应频率ω时的傅里叶分量,A对应频率ω时加速度信号的系数。
对加速度信号作积分运算得到速度信号:
(5)
再对速度信号作积分运算可得位移信号:
(6)
利用频域积分求位移信号时需要先对加速度信号进行傅里叶变换,对加速度信号的频域乘以-1/ω2得到位移的频域信号,再对位移的频域信号进行傅里叶逆变换,即可得到位移的时域信号。
1.3 正弦叠加信号仿真
以含噪信号:
a(t)=0.8sin (29πt2)+1.2sin (41πt)+2.0sin (63πt)+rand ()
为例,分别采用时域积分和频域积分的方法求取位移,结果如图1所示。可以看出,频域积分效果要好于时域积分,不易受噪声影响。
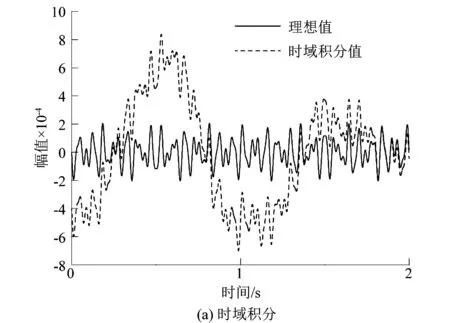
图1 含噪声信号时域积分与频域积分结果
2 测量系统程序设计
LabVIEW是一款图像化程序开发软件,广泛应用于测量系统的编写[12-13]。MATLAB作为一款强大的数学计算软件,可以实现复杂的数学算法。课题组借助LabVIEW和MATLAB开发了基于加速度频域积分的位移测量系统;利用LabVIEW实现加速度信号采集和处理;通过LabVIEW中的MathScipt窗口实现对MATLAB编写的加速度频域积分程序的调用。位移测量系统流程如图2所示。
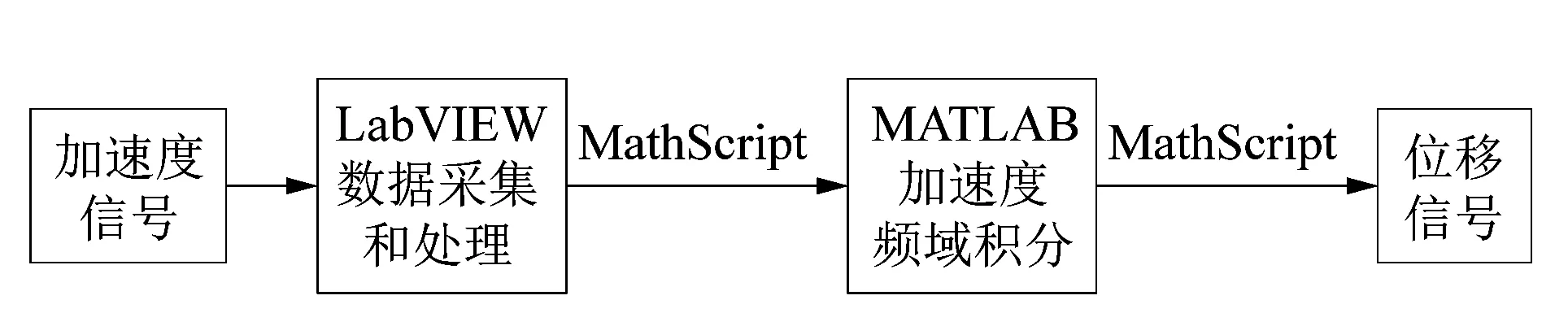
图2 位移测量系统流程图
3 频域加速度积分误差分析
在利用加速度频域积分求取位移时,需要进行频域滤波以及时域和频域的相互转化。为了更精确地得到位移测量结果,需要对加速度频域积分误差进行分析。
3.1 误差评价指标
为了对加速度信号积分结果进行评估,引入峰值误差和差值误差[14]:
(7)
(8)
式中:S′(t)为加速度积分求得的位移,S(t)为位移传感器测得的位移。
峰值误差Erp用来衡量S′(t)峰值相对于S(t)的峰值的误差;差值误差Err用来衡量[S′(t)-S(t)]的峰值相对于S(t)峰值的误差。
3.2 截止频率对频域积分结果的影响
以含噪声信号:
a(t)=0.8sin (29πt2)+1.2sin (41πt)+2.0sin (63πt)+rand ()
为例,选取不同的低截止频率进行频域积分,误差如表1所示。从表中可以看出,低截止频率对频域积分的结果影响较大,选取合适的低截止频率可以有效地滤除低频干扰。在实际应用时,可先通过频谱分析了解信号中所含有的频率成分,选取合适的低截止频率。
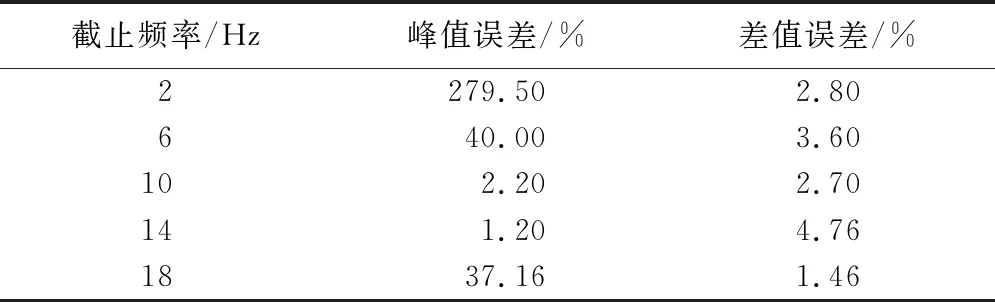
表1 不同截止频率下频域积分的误差
3.3 频率分辨率对频域积分结果的影响
以信号y=sin (2πft)+rand ()为例,分别对f=10.0和10.2 Hz的信号进行频域积分,取采样频率fs为1 000 Hz,采样点数N为1 000,结果如图3所示。可以看出,2个信号均为低频信号且频率相近,但积分结果相差较大。这是由于信号的频率分辨率为Δf=fs/N=1 000/1 000=1 Hz引起的,当f=10.2 Hz时,f不为Δf的整数倍,即没有做到整周期采样从而产生了栅栏效应,造成频域成分丢失。在实际工程应用时可通过选择合适的采样频率fs和采样点数N来提高频率分辨率,以尽可能地整周期截取信号来减小栅栏效应所带来的误差。

图3 不同频率信号的频域积分结果
4 有效性验证实验
4.1 基于DIC方法的振动位移测量实验
数字图像相关方法(digital image correlation,DIC)通过计算物体变形前后数字图形的相关性来获取感兴趣区域的位置信息,常用于物体表面位移和应变的测量[15]。DIC对实验环境要求极为宽松,并且具有全场测量、抗干扰能力强以及测量精度高等优点。因此可以利用高速相机对振动的物体进行连续拍摄,实现对振动位移的精确测量。基于DIC的振动位移测量系统如图4所示。

图4 振动位移测试装置
通过将本系统测得的位移与DIC方法测得的位移进行比较,可以对本系统的有效性进行验证。测量时在振动平台上放置加速度传感器和散斑图片用来测量振动平台竖直方向上的振动位移,设置加速度信号的采样频率为1 000 Hz,DIC的拍摄间隔分别设置为66和100 ms。
4.2 测量结果分析
由于实验过程中位移测量和加速度测量不是同一测试系统,很难保证加速度信号和位移信号在时间轴上的同步。因此后续对数据进行处理时按照DIC测量的结果在本系统测得的位移信号中提取对应的值,以确保二者在时间轴上尽量保持一致。测量结果与测量误差如表2和图5所示。可以看出,课题组开发的基于加速度频域积分的位移测量系统测量的位移结果与DIC的测量结果基本吻合,测量误差较小,可以满足实际的工程需求。

表2 DIC与加速度频域积分测量误差

图5 DIC与加速度频域积分测量结果
5 结论
针对某些场合下难以利用位移传感器对振动位移进行测量的问题,课题组选用加速度积分的方法来测量振动位移。通过仿真和实验得出以下结论:
1) 频域积分可以避免二次积分所带来的误差,相较于时域积分具有更高的稳定性;
2) 频域积分的误差主要取决于低截止频率和频率分辨率,可以通过选择合适的低截止频率以及提高采样频率来减小误差;
3) 利用LabVIEW和MATLAB联合编程开发的基于加速度频域积分的位移测量系统具有较高的测量精度,可以满足实际测量要求。

