强基计划数学备考系列讲座(10)
——圆锥曲线探究求解路径
王慧兴正高级教师 特级教师
(清华大学附属中学)
1 知识与技能
1.1 要点全览

表1
1.2 要点解析
1)定义
现行高中数学教材中删除了椭圆与双曲线的准线,这样导致离心率就沦为一个比值,失去了其几何意义,但高校强基校考坚持完整检测圆锥曲线的焦点、准线与离心率.



表2




表3

图2
6)阿波罗尼斯圆
给定两点A,B与常数k>0,且k≠1,则满足|PA|=k|PB|的动点P的轨迹是一个圆,称为阿波罗尼斯圆.


图3



表4
8)极点、极线

(2)椭圆、双曲线、抛物线对应的极点极线、配极原则以及自极三角形如图5、图6、图7所示.

图4

图5
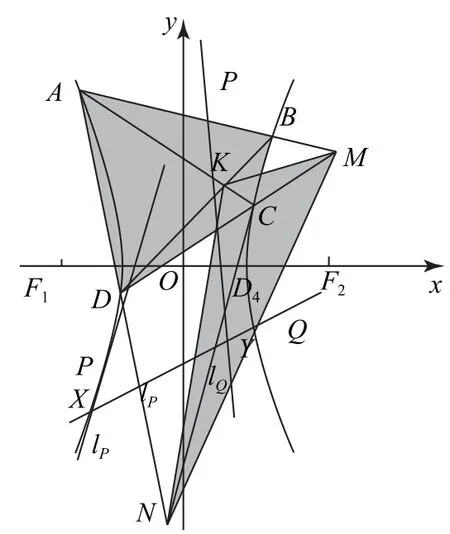
图6

图7
2 探究求解路径
2.1 基于概念

2.2 直线与曲线
1)方程分析
例2 如图8所示,在平面直角坐标系xOy中,F是x轴正半轴上一个动点,以F为焦点、O为顶点作抛物线C.设P是第一象限内C上的一点,Q是x轴负半轴上一点,满足PQ为抛物线C的切线,且|PQ|=2,圆O1,O2均与直线OP相切于点P,均与x轴相切.求点F的坐标,使得圆O1与圆O2面积之和S的值最小.

图8

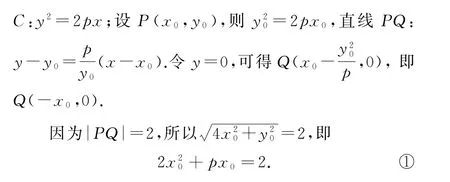

图9



3)典型结论
诸如“阿基米德三角形”“彭色列闭合定理”“对称性生成平行弦”“垂直弦生成定点弦”“阿波罗尼斯圆”等典型结论,多次成为命题立意的题材.


图10

2.3 极点极线


图11


2.4 仿射变换
通过仿射变换可以把圆与椭圆关联起来,把椭圆情境转化为圆的情境,借助圆的几何性质能够简化椭圆中繁杂的计算.


图12

2.5 组合分析

对于①,抛物线及其内部仅覆盖该直线上的一段线段;对于②,抛物线及其内部仅覆盖该直线上的一个点;对于③,抛物线及其内部不能覆盖该直线上的任意一点.
根据以上三种情况,我们知道用有限多条抛物线及其内部不能覆盖与这有限多条抛物线的对称轴均不平行的直线,而平面中存在这样的直线.于是,用有限多条抛物线及其内部不能覆盖一条直线,当然不能覆盖整个坐标平面.

本例表现抛物线的几何性质,检测考生组合分析能力.
3 实战演练



图13
7.(北京大学)A,B为y=1-x2上在y轴两侧的点,求过A,B两点的切线与x轴围成的三角形面积的最小值.
8.(浙江大学)已知点P(3,1),抛物线x2=4y上存在相异两点A,B,使得四边形PAQB是矩形,则点Q的轨迹方程是________.

11.(北京大学)如图14所示,用一个平面截一个等边圆柱(高等于底面直径),截面是椭圆,并且与圆柱底面仅有一个公共点.现沿着母线展开圆柱侧面,则展开面的交线形状是________.

图1
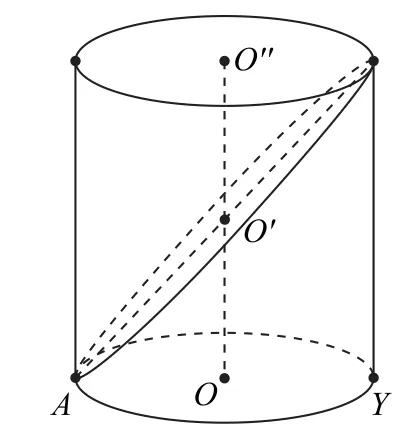
图14


