从通性通法的角度分析2022年新高考Ⅰ卷中的解析几何试题

金钟植正高级教师 特级教师

(广东省广州市白云中学)

2022年高考结束后,考生和社会各界普遍认为今年全国卷的几套数学试题特别难.但是,笔者认为看似很难的数学试卷中,并没有出现“偏、怪、难”的试题.每道试题考查的都是基础知识点和基本技能,即如果从“以不变应万变,注重数学通性通法”的角度进行备考,考生不会认为数学试题很难.下面以新高考Ⅰ卷中的解析几何试题为例,分析如何从数学通性通法的角度求解高考数学试题.

例1 (2022年新高考Ⅰ卷11,多选题)已知O为坐标原点,点A(1,1)在抛物线C:x2＝2py(p＞0)上,过点B(0,－1)的直线交C于P,Q两点,则( ).

A.C的准线为y＝－1

将直线AB的方程y＝2x－1 代入x2＝y,得x2－2x＋1＝0,解得x＝1,所以AB与C相切,故B正确.

由题知直线PQ的斜率一定存在,则可设直线

分析 如图1 所示,根据轴对称性的转化及椭圆的性质,不难发现,要求△ADE的周长,只需求长轴长的2 倍即可.离心率可确定椭圆标准方程及焦点横坐标中三个参数的比值,又因已知弦长|DE|＝6,故可根据坐标法求解相关参数的值.

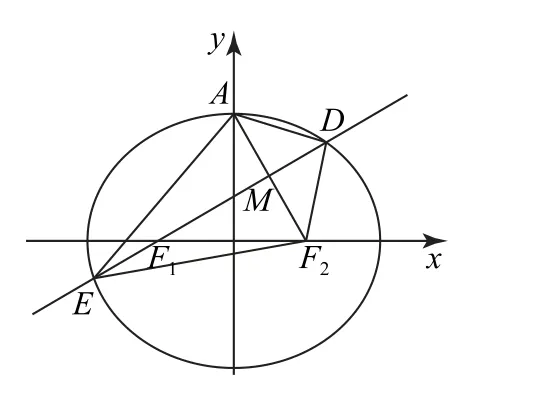
图1

分析 对于第(1)问,从题设看,要求直线l的斜率,从“直线AP,AQ的斜率之和为0”入手,有两个切入点:一个切入点是设含两个参数的直线l的方程,并将之与双曲线联立,再用“斜率之和为0”的条件构造含参数的方程,根据这个方程代数结构的特殊性求出斜率;另一个切入点是直接设出直线AP,AQ的方程(只含斜率一个参数),并与双曲线联立即可将P,Q两点的坐标用一个参数表示,通过斜率的比值“约掉”参数,两种方法本质上都属于坐标法.

对于第(2)问,根据题设和三角公式不难算出直线AP,AQ的斜率,进而可确定P,Q两点的坐标,最后利用弦长公式及三角形面积公式求解.

以上从数学通性通法的角度分析了2022年新高考Ⅰ卷中解析几何试题.从中不难发现,只要平时在备考中注重了数学通性通法,不管如何命题,应对高考是没有任何问题的.除了解析几何部分,考生普遍反映2022年新高考Ⅰ卷中的第18 题也是一道很难的题目,但仔细观察题目中的条件,只要懂得三角变换中的通性通法,即关注三种结构:角的结构、函数名的结构以及运算形式的结构,解决这个问题还是比较容易的.总之,要在高考中取得好的成绩,就要在高三备考中始终关注数学通性通法.