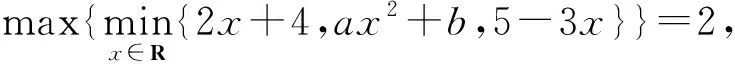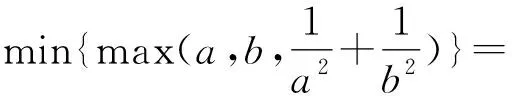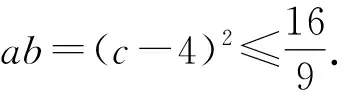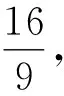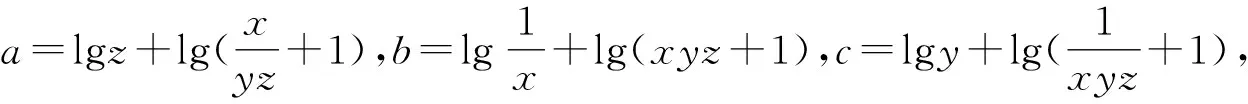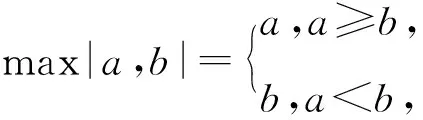数学竞赛中的复合最值问题

孙丽霞

(甘肃省天水市田家炳中学 741000)

复合最值问题出现在数学竞赛中历史悠久，直到现在还风靡在高考、自主招生和竞赛中，

初次接触的学生理解起来较难，其实就是求出函数f(x)的最小(大)值，记为f(x)min(f(x)max)，其中表达式还含有变量x或其它变量，再求f(x)min(f(x)max)的最大(小)值，可记为max{min[f(x),g(x)]}(min{max[f(x),g(x)]})，有时是两个(或多个)函数在某个特定区间进行动态比较，采用如下记号max{min[f(x),g(x)]}或者min{max[f(x),g(x)]}，用通俗的语言说就是“函数图象y=f(x)与y=g(x)，谁低取谁，再对图象求最高点的值”或者“函数图象y=f(x)与y=g(x)，谁高取谁，再对图象求最低点的值”.如果y=f(x)与y=g(x)的图象不是很好画，那就要用不等式知识，这就要掌握一定的解题技巧，用心领悟琢磨.

解析当a≤0时,f(a)=(a+1)2-2(a+1)-1=a2-2;

当a≥1时，f(a)=a2-2a-1;

当0

所以f(a)在[-1,1]上的最大值为-1.

A.-1 B.1 C.2 D.3

解析直线y=2x+4,y=5-3x分别经过(-1，2)，(1，2)，且这两点关于y轴对称，所以当b=0时，抛物线y=ax2过(-1，2)，(1，2)两点，得a=2;

当b≠0时，抛物线y=ax2+b过(-1，2)，(1，2)两点，所以a(-1)2+b=2.所以a+b=2.

例3 (2015年浙江省数学竞赛13)设函数f(x)=min{x2-1,x+1,-x+1}，其中min{x,y,z}表示x,y,z中的最小者.若f(a+2)>f(a),则实数a的取值范围为____.

解析当a+2≤-1时，a

当-1

此时有f(a)≤f(-2)=-1

当0≤a+2≤1时，-2≤a≤-1,

此时有f(a)≥f(a+2);

当1

此时有f(a)

当a+2≥2时，a≥0,

此时有f(a)≥f(a+2).

所以实数a的取值范围为(-∞,-2)∪(-1,0).

下面一题与例4有异曲同工之妙，只是在记号上面做一点花样，使有些同学看不明白.

例5 (2020年重庆赛区预赛6)若x,y为实数，则|2x+y|,|x-y|,|1+y|这三个数中最大数的最小值是____.

解析令M=max{|2x+y|,|x-y|,|1+y|},则

M≥|2x+y|,M≥|x-y|,M≥|1+y|.

所以6M≥|2x+y|+2|x-y|+3|1+y|

≥|(2x+y)-2(x-y)-3(1+y)|=3,

和例4相比，此例消元难度要大些，一方面要用到绝对值三角不等式，另一方面要配凑系数能消去变量x,y，又要保证等号取到.

解析根据柯西不等式， 有

例7 (2017年山东赛区预赛5)设a,b,c为非负实数，满足a+b+c=8,ab+bc+ca=16.记m=min{ab,bc,ca}，则m的最大值为____.

解析不妨设a≤b≤c，则

ab≤ca≤bc,m=ab.

转化为只要求ab最大值，结合已知条件

a+b=8-c,

ab=16-(bc+ca)=16-c(a+b)=(c-4)2,

进而只要求得c的范围，也就求得ab的最大值.

而a+b,ab同时出现又暗示逆用韦达定理构造a,b为实根一元二次方程，再用判别式求c的范围.

以a,b为实根的一元二次方程是

x2+(c-8)x+(c-4)2=0,

Δ=(c-8)2-4(c-4)2≥0,

解析此题历史悠久，即便放在现在依然是难题，并且有很强的指导意义，弃之不用是该题的最大技巧.

故M的最小值为lg2.

练习2 (2001年北京市数学竞赛题)设a,b,c∈R,且a+b+c=1,则min{max{a+b,b+c,a+c}的值为____.

练习3 定义max{a,b,c}为a,b,c中的最大值，令M=max{|1+a+2b|,|1+a-2b|,|2+b|},则对任意的实数a,b,M的最小值为____.

练习5 求min{max{x2+xy+x,4y2+xy+2y}}的值.

练习8 设x,y∈R,A=max={|x+y|,|x-y|,|1-x|,|1-y|},试求A的最小值.