关注立体几何常考题型
章莹莹
(江苏省新海高级中学 220006)
必修二教材所学立体几何知识,主要考查学生的空间想象能力、逻辑推理能力以及运算求解能力,同时又突出地体现了“数形结合思想”“转化思想”“分类与整合思想”等数学思想方法在解题中的灵活运用能力.关注立体几何这部分知识在试题中一般是如何考查的,有利于帮助同学们巩固基本知识,理清常用思想方法,进而提高学习的针对性和有效性.
1 考查空间的点、线、面之间的位置关系
例1 设α,β,γ是两个不同的平面,m,n是两条不同的直线,有以下四个命题:
①若α⊥β,m∥α,则m⊥β;
②若α∥β,α∥γ,则β∥γ;
③若m∥n,n⊂α,则m∥α;
④若m⊥α,m∥β,则α⊥β.
上述命题中的真命题有( ).
A.①③ B.②④ C.②③ D.①④
解析考虑长方体,我们很容易找到反面例子,可说明命题①和③均不正确.根据平面与平面之间的平行传递性,可知命题②正确.根据直线与平面平行的性质定理以及平面与平面垂直的判定定理,可以证明命题④正确.从而,上述命题中的真命题有②④.故选B.
反思与总结关于空间点、线、面位置关系的判断,一般来讲,如果要说明所给位置关系是正确的,那么就需要利用相关的公理、判定定理、性质定理等加以具体证明;如果要说明所给位置关系是不正确的,那么只需要我们找出一个具体的反例即可(而找反例时,经常考虑的是正方体、长方体、三棱锥、圆柱等熟悉的几何体).
2 考查利用判定定理证明有关的平行、垂直问题
例2如图1所示,在直三棱柱ABC-A1B1C1中,棱A1B,A1C的中点分别为点E,F,点D在B1C1上,且满足A1D⊥B1C.

图1
(1)求证:直线EF∥平面ABC;
(2)求证:平面A1FD⊥平面BB1C1C.
证明(1)因为E,F分别为A1B,A1C的中点,所以EF是△A1BC的中位线,所以根据三角形中位线性质定理可得EF∥BC.
又因为直线EF⊄平面ABC,直线BC⊂平面ABC,从而根据直线与平面平行的判定定理即得直线EF∥平面ABC.
(2)根据直三棱柱ABC-A1B1C1,可得BB1⊥平面A1B1C1.
又注意到A1D⊂平面A1B1C1,
从而可得BB1⊥A1D.
于是,结合A1D⊥B1C,BB1∩B1C=B1,
根据直线与平面垂直的判定定理即得
A1D⊥平面BB1C1C.
又A1D⊂平面A1FD,
故由平面与平面垂直的判定定理得平面A1FD⊥平面BB1C1C.
反思与总结立体几何中证明有关平行或垂直问题时,由于试题主要考查的就是有关判定定理在解题中的灵活运用,所以需要优先考虑对应的判定定理,以便迅速找到具体的解题思路.此外,值得特别提醒的是:作为证明题,利用立体几何中有关平行或垂直的判定定理时,必须将理由书写完整,这是解答题规范书写的基本要求.否则,就会被适当扣分.
3 考查利用其他方式证明有关的平行、垂直问题
例3如图2所示,在直四棱柱ABCD-A1B1C1D1中,F是棱AB的中点,而E是棱AD上的一个动点,底面ABCD是等腰梯形,且满足AB∥CD,AB=2CD,求证:直线A1E∥平面FCC1.

图2
证明因为由题意知

所以可知四边形AFCD是平行四边形.
从而可得CF∥AD.
又直线CF⊂平面FCC1,直线AD⊄平面FCC1,
从而可得AD∥平面FCC1.
①
根据直四棱柱ABCD-A1B1C1D1,
可得CC1∥DD1.
又因为直线CC1⊂平面FCC1,
直线DD1⊄平面FCC1,
从而可得DD1∥平面FCC1.
②
于是,根据①②及AD∩DD1=D,
可知平面AA1D1D∥平面FCC1.
又因为直线A1E⊂平面AA1D1D,
所以根据面面平行的性质即得直线A1E∥平面FCC1.
反思与总结证明立体几何中有关平行或垂直问题时,如果对应的判定定理不能够直接运用,那么就需要我们去考虑其他的证明途径.例如:要证明线面平行就可以先证面面平行,再利用面面平行的性质.再例如:要证明线面垂直就可以先证面面垂直,再利用面面垂直的性质.
4 考查“转化思想”在解题中的灵活运用


图3
解析如图3所示,作出正三棱锥P-ABC的侧面展开图,则△AEF的周长就是折线段AEFA′的长.
又结合图形知折线段AEFA′的长的最小值为线段AA′的长.从而,本题即求线段AA′的长.
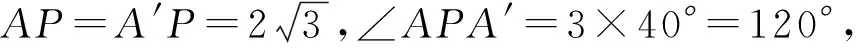
故所求△AEF周长的最小值为6.
反思与总结立体几何中遇到有关求最小值问题,往往不能直接求解,而需要先考虑其对应的侧面展开图,从而便于我们将不熟悉的“立体几何”问题转化为熟悉的“平面几何”问题,显然有利于目标问题的进一步分析与顺利求解.
5 考查“分割组合思想”在解题中的灵活运用
例5如图4所示,已知△ABC,满足∠C=90°,∠A=30°,BC=1.在△ABC内挖去一个半圆,且半圆的圆心O在边AC上,半圆与边BC,AB分别相切于点C,M,与边AC交于点N,那么图中阴影部分绕直线AC旋转一周所得旋转体的体积为____.

图4
解析根据题意,可知得到的旋转体是一个圆锥中挖去了一个球.
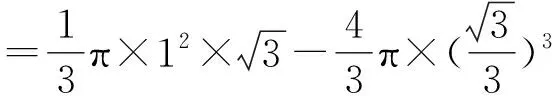
反思与总结处理立体几何中有关体积计算问题,一般比较简单的情形就是能够直接利用相关体积公式加以求解.而对于比较复杂的情形,就需要我们灵活运用“分割组合思想”去分析、解决问题.
以上,通过归类解析的形式,着重归纳总结了必修二立体几何部分有关常考题型.结合具体例题的剖析,可帮助学生加深对教材中有关公理、判定定理、性质定理的准确理解,提高对相关数学知识、思想方法的整合与运用能力,拓宽解题思维视野,积累解题经验,从而提升直观想象、逻辑推理与数学运算方面的核心素养.

