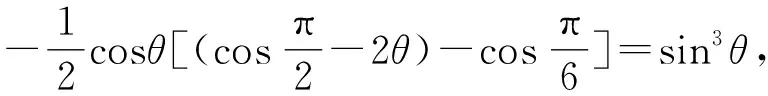对“布洛卡点”几何模型的几点思考
金 毅
(内蒙古自治区呼和浩特市第二中学 010000)
布洛卡点是一类重要的几何模型,在很多与几何有关的问题中有重要应用.我们从布洛卡点的定义出发展开思考.
1 对布洛卡点定义与存在性的思考
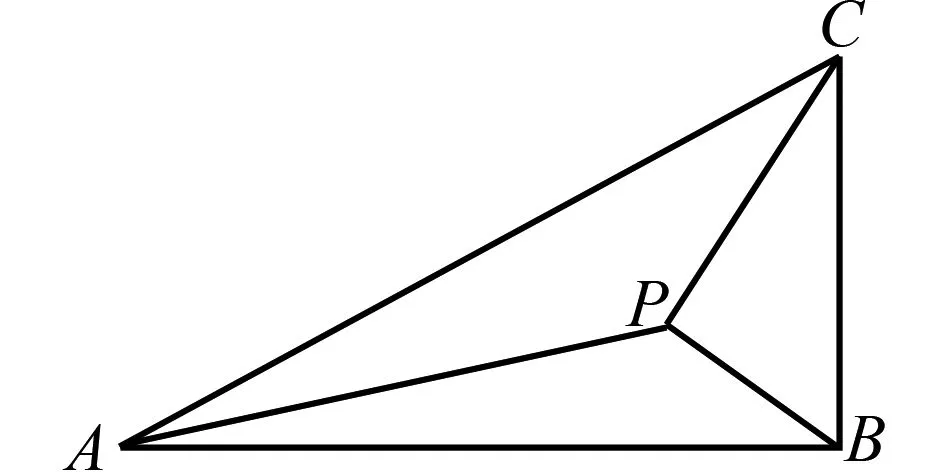
命题1(布洛卡点定义)如图1,已知△ABC中,P是内部一点,当∠PAB=∠PBC=∠PCA=θ时,点P为△ABC的布洛卡点.角θ为布洛卡角.

图1
思考在此定义中,我们有两点疑问.一是对任意的三角形,是否一定有布洛卡点?二是如果存在,如何找到布洛卡点?我们将通过以下命题来进行探究.
命题2(布洛卡点的存在性)如图2,在锐角△ABC中,过点A作垂直于AB的直线l,过点B作垂直于BC的直线m,过点C作垂直于AC的直线n,其中,l∩m=D,m∩n=E,n∩l=F,作△ABD,△BCE,△ACF的外接圆,证明:三圆共点于P,且∠PAB=∠PBC=∠PCA.

图2

故∠APC+∠APB=2π-∠AFC+∠ADB.
即∠AFC+∠ADB=2π-∠APC+∠APB=∠BPC.
同时∠AFC+∠ADB=π-∠BEC.
所以∠BPC=π-∠BEC.
故B,E,C,P四点共圆,则这三圆共点于P.
接下来证明角相等.
在圆APBD中,可得
根据BD⊥BC,可得
所以∠PAB=∠PBC.
同理,可以证得∠PAB=∠PCA.
综上,∠PAB=∠PBC=∠PCA.


图3

所以B,P,C,E四点共圆.则三圆共点于P.


所以∠PAB=∠PBC.

由此,我们得到,布洛卡点的存在性与三角形形状无关,也即对任意形状的三角形均存在布洛卡点,这是非常重要的.同时,通过对命题2的研究,我们也得到了在任意三角形内寻找布洛卡点的方法.
2 对布洛卡点性质的思考
从定义出发,我们进一步思考,提出若干命题,对布洛卡点的性质进行拓展延伸.
命题3如图1,已知△ABC中,BC=a,AC=b,AB=c,P是布洛卡点,则有等式cotA+cotB+cotC=cotθ成立.
证明如图1,根据命题1,可得
∠PAB=∠PBC=∠PCA=θ.
设△ABC的面积为S,且AP=x,BP=y,CP=z,

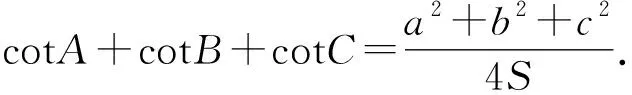



对以上cotθ三式使用合比定理,得
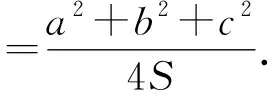
命题4已知△ABC中,P为布洛卡点,当A=2θ时,则有a2=bc.



所以a2=bc成立.


图4
证明根据命题3,有


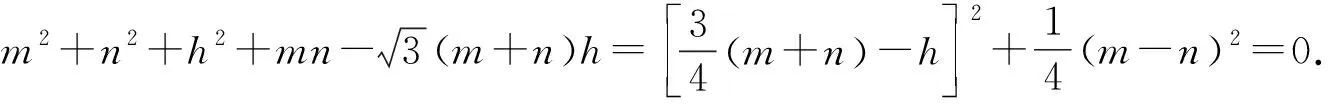


综上,△ABC为等边三角形.
命题6在△ABC中,∠PBA=∠PBC=∠PCA=θ,则有θ≤30°

思考本例说明三角形中布洛卡角的取值范围不会超过30°.并且根据命题5,当布洛卡角恰好取到30°时,此时△ABC为等边三角形.
命题7 在锐角△ABC中,∠PBA=∠PBC=∠PCA=θ,有不等式tanA+tanB+tanC>cotθ成立.
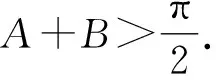
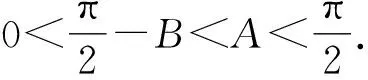

同理,可得cotC 以上相加,可得 cotA+cotB+cotC 根据命题3,即tanA+tanB+tanC>cotθ成立. 根据命题3,a2+b2+c2=4Scotθ. 命题9 在△ABC中,∠PBA=∠PBC=∠PCA=θ,有不等式2cotθ≥cscA+cscB+cscC成立. 证明根据a2+b2+c2≥ab+ac+bc,可得b2+c2-a2+a2+c2-b2+a2+b2-c2≥ab+ac+bc,2bccosA+2accosB+2abcosC≥ab+ac+bc. 根据正弦定理,可得 2sinBsinCcosA+sinAsinCcosB+sinAsinBcosC ≥sinAsinB+sinAsinC+sinBsinC. 不等式两边同除sinAsinBsinC,可得 2cotA+cotB+cotC≥cscA+cscB+cscC. 根据命题3,可得2cotθ≥cscA+cscB+cscC成立. 图5 分析当∠APB=150°时,∠APC=120°,可知∠PCA+∠PAC=∠PCA+∠PCB=60°. 所以∠PAC=∠PCB. 同理可得∠PAB+∠PBA=∠PAB+∠PAC=30°. 所以∠PBA=∠PAC. 设∠PAC=∠PBA=∠PCB=θ,可知点P为△ABC的布洛卡点. 根据命题2,可得cotA+cotB+cotC=cotθ. 思考本例首先通过证明∠PAC=∠PBA=∠PCB,说明点P是△ABC的布洛卡点,之后使用相关结论迅速解决∠PBA的正切值.当然,在这样的问题中,除了布洛卡点的性质之外,我们还可以使用“角元塞瓦定理”,也即 这说明布洛卡点的模型也可用塞瓦定理处理. 布洛卡点是平面几何中非常重要的几何模型,总结本文,有几点需要重点关注. (1)布洛卡点对任意三角形均存在,是三角形内的等角点,因而可能得到角相等或者相似的结论. (2)布洛卡角和三角形的三个内角有密切联系,它们的三角函数值存在着很多相等与不等关系,这里有很多命题值得挖掘;布洛卡点的问题可以借助别的定理解决(如塞瓦定理等),在思考时要充分对数与形的关系进行结合.数与形是数学中永恒不变的主题,良好的结合会对数学思维有极大地提升,这也是思考数学问题的乐趣所在.

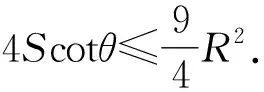

3 对布洛卡点模型应用的思考