运用函数思想证明不等式

甘肃省静宁县第一中学 鲍晓霞

函数是高中数学的重要内容之一，函数的思想和应用是贯穿整个高中数学的一条主线.运用函数的概念和性质去分析问题、转化问题和解决问题，这种思路就是函数思想.不等式也是高中数学的主要内容，它几乎涵盖了高中数学的各个领域，中学数学的各部分内容都与不等式有着千丝万缕的联系；由于不等式的证明类问题，对逻辑推理能力的要求较高，加之题型广泛，方法灵活，考查面广，深受命题者的青睐，既是近年来高考的热点问题，也是高中数学的重点和难点.人教版选修4-5的第二讲“证明不等式的基本方法”中，集中介绍和讲解了“比较法、综合法、分析法、反证法、放缩法”等常见的几种证明方法，在第四讲中还补充了“用数学归纳法证明不等式”等内容.看起来证明不等式的方法学得很多了，但是当我们用这些方法去证明一些非常规类不等式时，常常会感到力不从心，这也是许多考生对不等式证明题怀有畏难情绪的主要原因之一.看来我们还有必要学习和掌握一些应对非常规类不等式证明的方法与技巧.

运用函数思想证明不等式，就是应对那些非常规类不等式证明的一种策略，就是对那些本身没有明显函数关系的不等式，通过类比、联想、转化等方法，合理地引进函数[1]，并通过对所引进函数的定义域、值域、奇偶性、连续性、有界性等性质的研究，使不等式最终得证.

1 利用函数的单调性

函数的单调性，在具体的函数中不难判别；对有些涉及到数列以及以自然数n为变量的证明题时，如果能与函数的单调性联系起来，往往能够找到更简捷的证明方法.

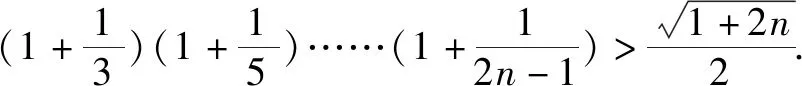
证明：当n>1,n∈N时，不妨令

f(n+1)

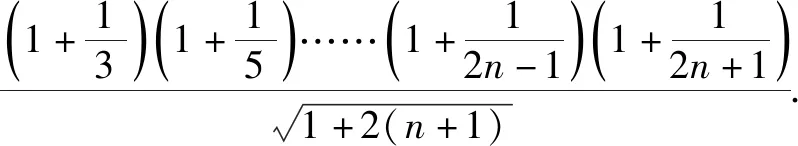
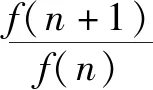
故f(n+1)>f(n).

即f(n)是单调增函数(n=2,3，……).

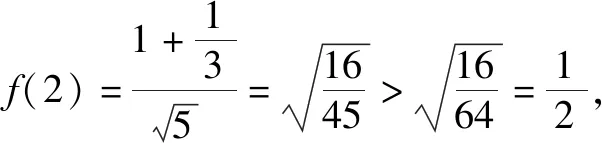
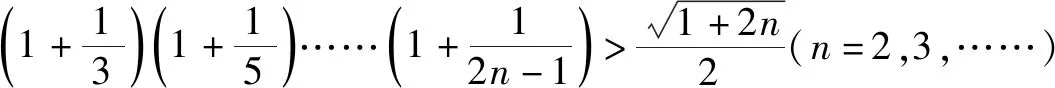
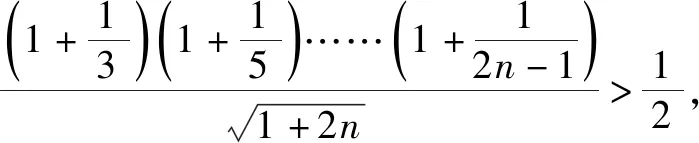
2 利用函数的奇偶性

利用偶函数的轴对称性和奇函数的中心对称性，常能使不等式的证明过程变得简捷，还能避免复杂的讨论.

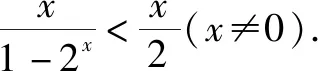
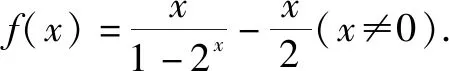
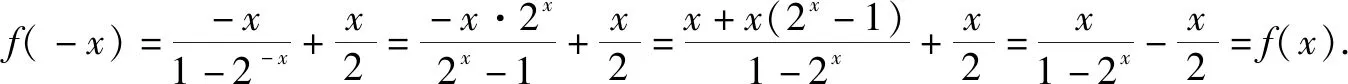
故f(x)为偶函数.

当x>0时，2x>1，即1-2x<0，则f(x)<0.

由偶函数的性质可知，当x<0时，亦有f(x)<0.

方法与技巧：本题先把不等式转化为函数，然后利用偶函数的对称性进行证明，收到了化繁为简的奇效.

3 利用三角函数的有界性

如果x∈R，那么|sinx|≤1，|cosx|≤1，这就是三角函数的有界性.对于一些与三角函数有关的不等式，如果能很好地利用其有界性，往往能够帮助我们快速找到解题的突破口，从而使问题顺利解决.

证明：因α，β为锐角，可把α，β，π-(α+β)看作三角形的三个内角，且其对边分别为a，b，c.

因为|sin(α+β)|≤1，所以sin2α+sin2β=sin(α+β)≥sin2(α+β)=sin2[π-(α+β)].

根据正弦定理，得a2+b2≥c2，从而可得

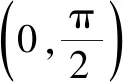
所以sin(α+β)=sin2α+sin2β>cos2β+sin2β=1，这与|sin(α+β)|≤1矛盾.

方法与技巧：从本题的证明过程可以看出，三角函数的有界性在证明不等式的过程中起到了关键的桥梁作用.所以说，运用正、余弦定理将边角关系进行巧妙转化，是函数思想的运用之妙.

4 利用二次函数的性质

根据二次函数f(x)=ax2+bx+c(a>0)，若Δ≤0，则恒有f(x)≥0；反之，若恒有f(x)≥0，则Δ≤0.依此来构造二次函数解题是常用的方法.

例4α，β，γ为任意三角形的三个内角，求证：x2+y2+z2≥2xycosα+2yzcosβ+2zxcosγ对于任意实数x，y，z总成立.

证明：令f(x)=x2-2x(ycosα+zcosγ)+y2+z2-2yzcosβ，则

Δ=4(ycosα+zcosγ)2-4(y2+z2-2yzcosβ)

=4y2(cos2α-1)+8yz(cosαcosγ+cosβ)+4z2(cos2γ-1)

=-4y2sin2α+8yz[cosαcosγ-cos(α+γ)]-4z2sin2γ

=-4y2sin2α+8yzsinαsinγ-4z2sin2γ=-4(ysinα-zsinγ)2≤0.

所以f(x)≥0.

故x2+y2+z2≥2xycosα+2yzcosβ+2zxcosγ.

方法与技巧：首先将待证的不等式整理变形为x的二次函数式f(x)=x2-2x(ycosα+zcosγ)+y2+z2-2yzcosβ≥0，只要能证明f(x)的图象不在x轴的下方即可.

5 利用二项式定理

除了直接使用二项式定理和适当变形后再运用二项式定理证明不等式的方法外，我们还可以通过利用二项式定理构造函数f(x)=(a+x)n(n∈N)的方法进行证明，这种方法在证明不等式、组合数恒等式、组合数求和等题型中得到广泛应用[2].

例5证明：当n≥3，n∈N时，2n≥2(n+1).

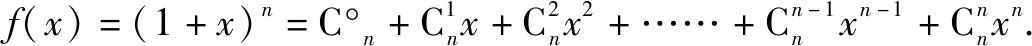
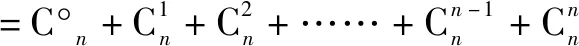
=2n.

当n=3时，2n=2(1+n)；

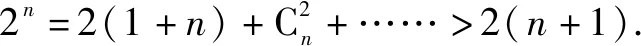
综上可知，当n≥3时，2n≥2(n+1).

方法与技巧：本题就是灵活运用二项式定理把不等式转化为函数，然后采用分步讨论证明方法的典型实例.

综上所述，证明非常规类不等式就要采用非常规的方法，运用函数思想证明非常规类不等式具有极大的便捷性与实用性，“运用之妙存乎一心”，在具体的解题过程中，我们要根据题目提供的信息灵活选择合适的方法与技巧进行证明，解题时既要充分利用已知条件和函数的性质，又要时刻牢记解题目标.