基于最大似然原理的电厂混煤均匀性确定

刘福国， 赵中华， 刘 科， 王守恩

(国网山东省电力公司 电力科学研究院, 山东 济南 250003)

1 引 言

为降低燃料成本或减少锅炉燃用煤与设计煤的偏差，发电厂入炉煤通常采用不同矿点的原煤掺混而成。入炉煤掺混质量是影响机组安全经济运行的最重要因素之一[1～9]，但至今缺少入炉煤混合状态的评价方法，限制了煤场掺混工作的改进和提高。

在医药、冶金、食品、化肥和建材工业中，粉体或颗粒状物料的良好混合也是决定产品质量的重要因素，例如食盐中碘的均匀性关系到千家万户的健康。这些行业的产品通常采用统计方法来评估物料的混合状态。

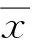
(1)

(2)

标准差σ反映了混合物某种成分含量的波动大小，因而，表明了混合物的均匀性。在对含量标准差σ进行了无量纲化处理后，得到混合指数M，它更清楚地表征物料的混合质量。M根据该成分的含量标准差σ计算[11]：

(3)

式中：当二元物料完全分离时，该种成分的标准差为σ0；当二元物料处于完全随机的均匀混合状态时，该种成分的标准差为σR。由式(3)可知，当σ=σ0，即二元物料完全分离时，M=0；当σ=σR，即二元物料完全均匀混合时，M=1。可见，M越大，混合均匀性越好。

完全分离状态的标准差σ0与该成分的含量P有关；完全随机的均匀混合物的标准差σR不仅与该成分的含量P有关，还取决于混合物中的颗粒数量N。σ0和σR的计算式为[11,12]：

(4)

(5)

对于给定的二元混合物，σR和σ0通常是固定的。因此，要测定混合指数M，主要是对混合物进行多次采样分析，确定某种成分的含量，再根据式(2)计算该成分含量的标准差σ。

煤本身是由多种成分组成的混合物，不同品种的煤，其主要成分为固定碳、挥发分、水分和灰分等。对于多个矿点原煤掺混而成的混煤，很难区分混煤中的某种成分(如固定碳)是来自哪个矿点，利用上述采样分析法无法确定混煤中某个矿点原煤的含量。因此，采用传统的采样分析法评估电厂混煤的混合质量存在较大困难，其它评价方法如数字图像分析、红外光谱和X射线法等[13，14]，在电厂入炉煤大规模的连续测量中也受到限制。

发电厂在日常运行中积累了大量的煤的工业成分数据。矿点原煤和入炉混煤中某种成分的概率分布的变化中包含了混合状态的信息。本文选取煤的某种成分作为示踪剂，考察该成分在矿点原煤和混煤中概率分布的变化，并采用数据挖掘算法从中提取了电厂入炉煤混合质量的信息，进一步研究了新开发的电厂入炉煤掺混质量评估方法的测量特性。

2 实际问题描述

以最常见的2个矿点原煤的掺混系统为例。如图1所示，煤1和煤2分别为来自不同煤矿的2种煤，它们每次入厂均需按规定采样，并对样品进行工业成分和发热量的测定。2种煤通过取料机或筒仓给料机，按预定比例向输煤皮带供煤，并在皮带上完成简单的掺混[8,15]。这种掺混方式决定了混煤中某种原煤含量的波动大小，同时，由于取/给料设备供料量的波动，也加剧了混煤中该种原煤含量的波动。

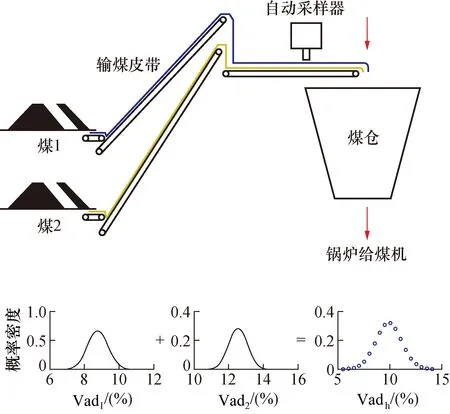
图1 入炉煤掺混示意图Fig.1 Schematic diagram of coal blending in power station

煤是一种复杂的混合物，即使是来自同一矿点的单一煤种，每次采样样品的工业成分也是变化的。对于同一矿点煤，当开采煤层稳定，虽然样品中某种成分的含量是波动的，但该成分含量的概率分布通常符合一致的统计规律[9,16]。矿点原煤中某种成分含量的概率分布可从积累的入厂煤化验数据中获得。对于图1的掺混过程，在掺混系统入口，给定2种矿点原煤挥发分Vad含量的概率分布，则混煤挥发分Vadh概率分布不仅决定于矿点原煤挥发分分布，还决定于掺配比例以及混合状态。在给定矿点原煤挥发分概率分布以及混煤挥发分数据样本的情况下，本文采用数据挖掘算法，求解混煤中某种矿点原煤含量的概率分布，进而对颗粒混合质量进行评估。需要说明的是，虽然图1中2种矿点原煤掺混比例在实际生产过程中可以大致设定，但掺混系统一般不配备矿点原煤流量测量装置，因此，运行中无法准确测定某种矿点原煤的含量。

3 矿点原煤成分的统计分布

在2018年底到2019年初，某发电公司超临界压力发电机组为控制入炉煤挥发分含量，发电用煤采用国内2个煤矿的原煤掺混而成。分别对这2种入厂煤在5个月内的采样数据进行统计分析，利用Matlab中的ksdensity函数得到固定碳FCad、挥发分Vad和发热量Qarnet等指标的概率密度分布见图2，图中还给出了以指标样本均值μ和σ标准差作为分布参数的正态分布的概率密度。由图2可以看出，各种成分和发热量的概率密度分布较为接近正态分布。对于煤种1和煤种2，挥发分的概率密度分别可近似用如下正态分布表示：

(6)

(7)

图2中给出了分布参数μ、σ的值。

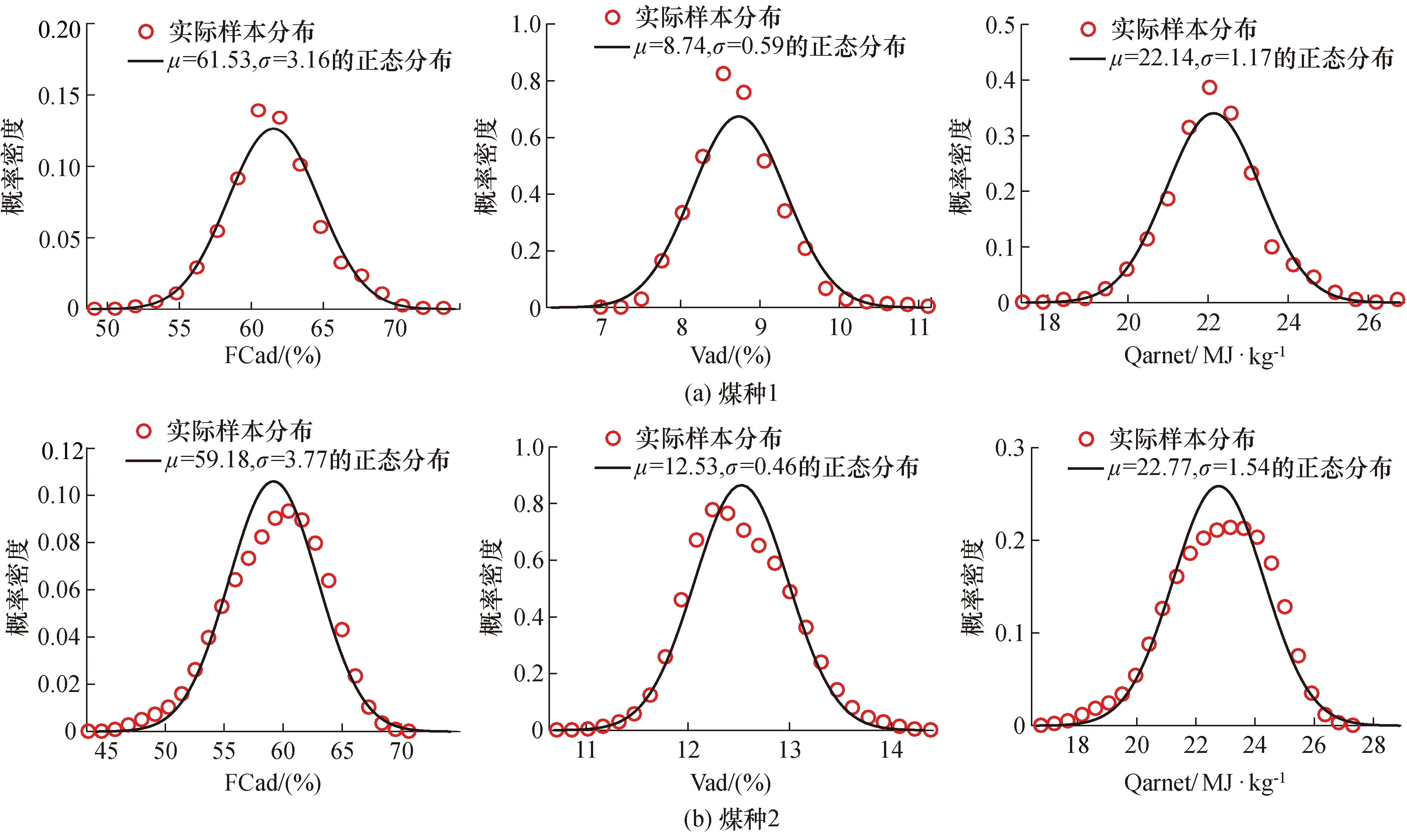
图2 2种入厂矿点原煤的固定碳、挥发分和发热量的概率分布Fig.2 Probability distribution of fixed carbon, volatile matter and calorific value of raw coal from 2 incoming ore points

4 混合模型

在图1掺混系统入口，给定矿点原煤的某种成分的概率分布，系统出口混煤中该成分的概率分布由掺配比例和混合状态唯一确定。混合模型就是在已知矿点原煤某种成分的概率分布以及混煤样本集的情况下，求解混煤中某种矿点原煤含量的概率分布，进而对混合状态进行评估。

4.1 混合过程的随机数学描述

以煤的挥发分成分为例。掺混系统入口2种矿点原煤挥发分的概率分布由式(6)和式(7)给出。将混煤中煤种1的含量看作随机变量，并假设其服从正态分布，即

(8)

式中：μr表示煤种1含量的均值;σr与式(2)所表示的混合标准差具有相同的含义，它表明了混煤中煤种1含量的波动大小。

分别给定煤种1和煤种2的一个样品，样品挥发分含量为X1和X2。若混煤中煤种1的含量为r,则煤种2的含量为1-r，混煤挥发分含量Z为:

Z=rX1+(1-r)X2=r(X1-X2)+X2

(9)

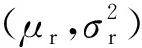
4.2 某种原煤含量和标准差的最大似然估计

已知混煤挥发分样本集，求解某种矿点原煤含量的均值μr和标准差σr的问题，是上述式(9)所表示的电厂混煤过程的反问题，可采用最大似然法对煤种1含量μr和标准差σr进行估计。

根据式(9)，若给定煤种1和煤种2的挥发分分布,见式(6)和(7)，则混煤挥发分含量Z的概率密度分布函数g(z)与掺混参数(μr,σr)有关:

g(z)=g(z,μr,σr)

(10)

根据式(9)，可推导Z的概率分布函数g(z,μr,σr)，其详细过程见第4.3节。

假如通过试验得到M个入炉混煤样品，由此得到M个挥发分含量为

(11)

式中zM是第M个样本的挥发分含量。

从概率密度分布为g(z)的总体中，抽取到这M个样品的概率，等于它们各自概率的乘积[17]，即

(12)

θ=(μr,σr)

(13)

式中：l(θ)称为联合概率，是掺混参数θ相对于混煤挥发分样本集的似然函数。

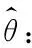
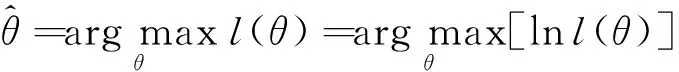
(14)

(15)

为方便计算，在式(14)中，将求取似然函数l(θ)的最大值，转化成求对数似然函数lnl(θ)的最大值。

(16)

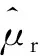
4.3 混煤挥发分概率密度分布函数g(z)

X1-X2=(μ1-μ2)+εX12

(17)

(18)

同理，得到

X2=μ2+ε2

(19)

(20)

以及

r=μr+εr

(21)

(22)

将上述式(17)中的X1-X2、式(19)中的X2和式(21)中的r代入式(9)，整理得到

Z=μr(μ1-μ2)+μ2+[μrεX12+(μ1-μ2)εr+ε2]

+εrεX12

(23)

令

Z1=μr(μ1-μ2)+μ2+[μrεX12+(μ1-μ2)εr+ε2]

(24)

Z2=εrεX12

(25)

则

Z=Z1+Z2

(26)

由于在式(24)中

μr(μ1-μ2)+μ2=常数

(27)

且根据正态分布随机变量的线性组合仍服从正态分布[16]，可得到

(28)

所以式(24)中的Z1服从如下正态分布

(29)

因此，Z1的概率密度函数为

(30)

式(30)中σH为

(31)

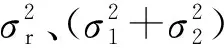
(32)

式中K0( )为第二类修正贝塞尔函数。

由式(26)可知，求式(9)所表示的混煤挥发分含量的概率密度函数g(z)的问题，转化为求随机变量Z1与随机变量Z2之和的概率密度函数的问题，其中Z1和Z2的概率密度分布分别见式(30)和式(32)。利用卷积公式[21]，得到随机变量Z1和Z2之和的概率密度g(z)为：

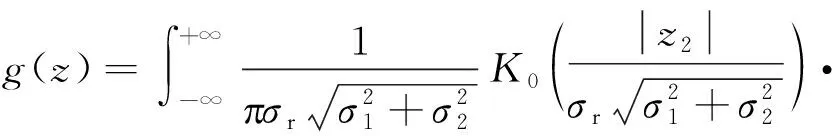
(33)

5 实际掺混系统求解

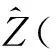
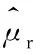
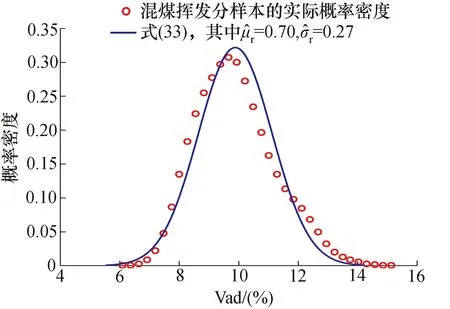
图3 样本的概率密度分布和式(33)的对比Fig.3 The comparison between the probability density distribution of samples and equation (33)

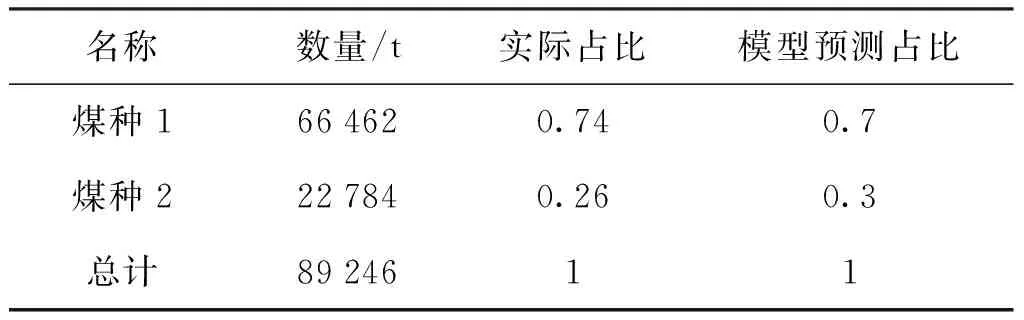
表1 2种煤的实际消耗量与预测值对比Tab.1 Comparison of consumption and predicted value of two kinds of coal

6 混合模型测量特性分析

如图1，当掺混矿点原煤不变时，电厂入炉煤掺混系统通常保持稳定运行状态，掺混参数(μr,σr)保持不变。若要改变实际掺混系统的参数(μr,σr)，进行混煤采样试验，机组将面临较大风险。因此，对于实际掺混系统，通常无法得到其它掺混状态(μr,σr)下混煤采样数据。

1) 设定式(8)中(μr,σr)的值，利用Matlab的normrnd函数，产生混煤中煤种1含量r的正态分布随机数；

2) 利用式(6)和式(7)给定的矿点原煤分布，根据同样的方法，产生矿点原煤挥发分含量的正态分布随机数；

3) 将上述随机数代入式(9)，得到混煤挥发分含量仿真数据。

对于图2的2种矿点原煤，表2给出了不同掺混参数(μr,σr)下的实际值。由表2可以看出：μr的估计值和实际值吻合较好，当σr>0.2时，σr的估计值和实际值偏差小于0.05，σr越大，σr估计偏差越小；但当σr较小时(σr<0.15)，σr的估计值和实际值的偏差稍大，σr越小，σr估计偏差越大。

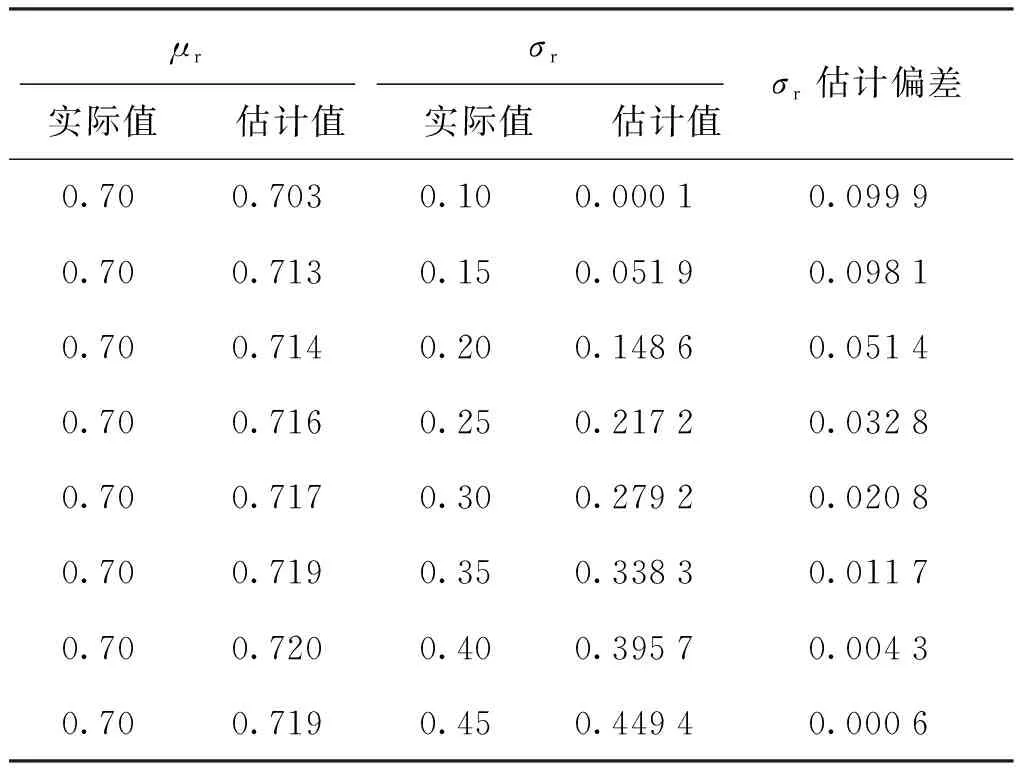
表2 掺混参数的计算值和实际值对比Tab.2 Comparison of calculated and actual mixing parameters

由图4可以看出，当σ2从0.46降低到0.30，即(σ1-σ2)从0.13增大到0.29后，图中坐标点更靠近图中的y=x线，这表明σr的估计偏差减少。因此，(σ1-σ2)越大，σr的估计偏差越小；(σ1-σ2)越小，σr的估计偏差越大。

从图4还可看出，当σ2不变，即对于同样的矿点原煤分布，σr越小，数据点偏离直线y=x越多，这表明σr的估计偏差越大。因此，σr越小，即混合质量越好，σr的估计偏差越大；σr越大，即混合质量越差，σr的估计偏差越小。

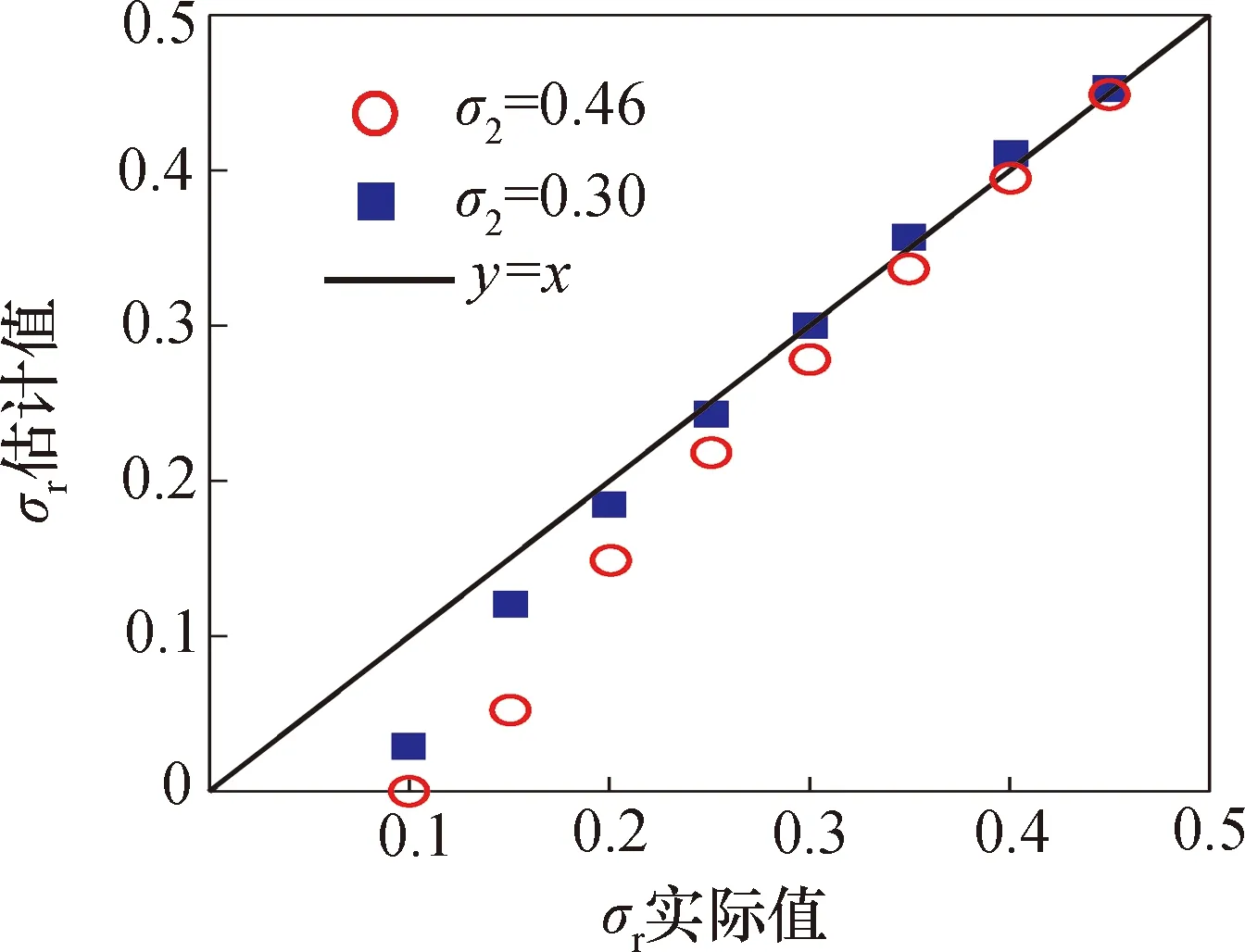
图4 σr估计值和实际值的对比Fig.4 The comparison between the estimated value of σr and the actual value

与其它行业相比，电厂对入炉煤掺混系统混合质量的要求相对较低。当σr较大，即混合质量较差时，是掺混系统应重点监控的区间，本文给出的掺混模型在这一区间具有较好的精度，能够满足测量要求。

7 总 结

(1) 矿点原煤是各种成分符合不同概率分布的混合物，混煤中某种成分的概率分布由矿点原煤中该成分的分布、掺混比例和混合状态共同决定。

(2) 采用挥发分作为考察从矿点原煤到混煤的概率分布变化的示踪成分，本文给出了已知矿点原煤挥发分分布和混煤挥发分数据集，对矿点原煤含量和含量标准差进行最大似然估计。

(3) 所给出掺混模型对实际掺混系统的预测结果与矿点原煤消耗量的统计数据吻合良好。

(4) 对于混合质量较差的掺混系统，掺混模型具有良好的预测精度，而当掺混系统的混合质量较好时，掺混模型的预测精度偏大;当掺混系统混合质量较差时，应重点加强监测。