基于收缩流动的气体超声流量计声道稀疏化及测量方法

毛显谊, 崔骊水, 谢代梁

(1. 中国计量大学 计量测试工程学院, 浙江 杭州 310018; 2. 中国计量科学研究院, 北京 100029)

1 引 言

气体超声流量计[1～4]因其非接触测量、压损小、测量精度高等优势,逐渐成为天然气计量中的主力仪表[5],并在国际天然气贸易中广泛应用。但气体超声流量计测量原理为速度面积法[6]，因此其测量准确度直接受到流场品质的制约[7]。为了满足天然气贸易交接对流量计量准确度水平的要求,多采用对复杂流场或不规则流动适应性更强的多声道超声流量计,而声道数的增加必然导致成本上升。

在封闭管道中建立收缩流动[8]可以在一定程度上控制流场中的流速分布情况,提高主流区均匀性,达到改善流场品质的目的。若将收缩结构应用于超声流量计测量,便可获得均匀的高品质流场,减少流场的复杂性与多样性,这样气体超声流量计便不需要额外考虑其对不同复杂流场的适应性问题。然而对收缩结构的研究大多集中在射流流场[9],对不同收缩比的收缩结构在管道流场中的相关流场特征的研究较少,同时收缩流场与传统超声流量计算模型不匹配,会造成较大误差。

本文通过数值仿真方式,对不同收缩比的收缩结构下流场特征进行分析,提出并设计与其匹配的流量计算模型和声道安装方式,进而通过实流实验对气体超声流量计的测量准确度进行研究,探讨基于收缩流动气体超声流量计声道稀疏化的可行性。

2 超声流量计计算模型

时差法超声波流量计的测量原理如图1所示。超声波流量计通过测量超声波脉冲顺流、逆流传播时间差来进行流量计量[10]。设超声波在静止流态流场中的传播速度为c,当流体速度为v时,通过测量声波在顺逆流传播的时间td和tu,可得到流体的流速vz:

(1)

(2)

(3)

式中:L为换能器之间的距离;θ为声道与管道轴线之间的夹角,即声道角;D为管道直径。

图1 超声波在流体中传播特性示意图Fig.1 Schematic diagram of ultrasonic wave propagation characteristics in fluid

(4)

通过对所有声道速度加权即可计算出流量qv:

(5)

式中:Wi为各声道权重系数,其数值取决于所采用的积分算法;vi为各声道所测的分速度,i表示第i声道。

3 基于收缩结构的流场构造研究

流体流经渐缩管,流速沿轴向稳定加速[12],并形成为中间平,两边速度急剧增加,类似梯形的收缩流场(下文均称为收缩流场)。其核心区域速度均匀性较高,这时测量小部分区域流速即可表征整个核心区域的流速分布,可以满足气体超声流量计测量时对流场的要求。

利用渐缩管对流场进行主动控制,形成满足气体超声流量计测量要求的收缩流场。将气体超声传感器侵入流场并安装,使其信号发射、接收端处于流场品质较高的核心区域,可减少流速波动对超声测量的影响。通过流速修正模型将声道所测流速转化为管道截面的面平均流速,从而获得精确的流量值。1) 采用数值模拟研究不同收缩比下收缩流动的流场特征,选取适合实际要求的收缩结构。2) 在所选收缩结构的基础上分析初始流速大小与流场边界层厚度以及流速分布的关系,从而确定气体超声传感器的安装方式,推导出对应的流速修正模型。

3.1 收缩比选取

设计如图2的数值模拟模型,其收缩比C分别为2∶1,2.25∶1,4∶1,6∶1,保持下游管道直径D=100 mm不变,上游管道直径随收缩比的变化而变化,其值为C×D。选用标准的k-epsilon湍流模型;采用分离隐式求解器[13];压力速度耦合采用Simple算法;压力、动量、湍流度方程采用一阶迎风格式。

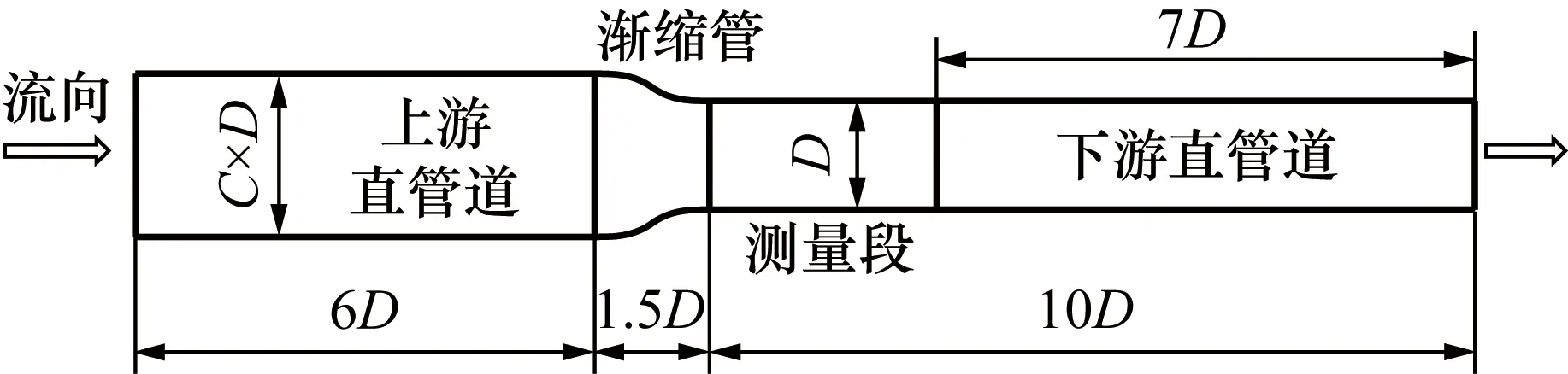
图2 二维结构示意图Fig.2 Two-dimensional structure diagram

由Fluent仿真得到的不同收缩比下的流速分布如图3、图4所示,流体流经渐缩管,流速沿轴线稳定加速,形成了核心区流速均匀性较高的收缩流场,流速分布差异不大。

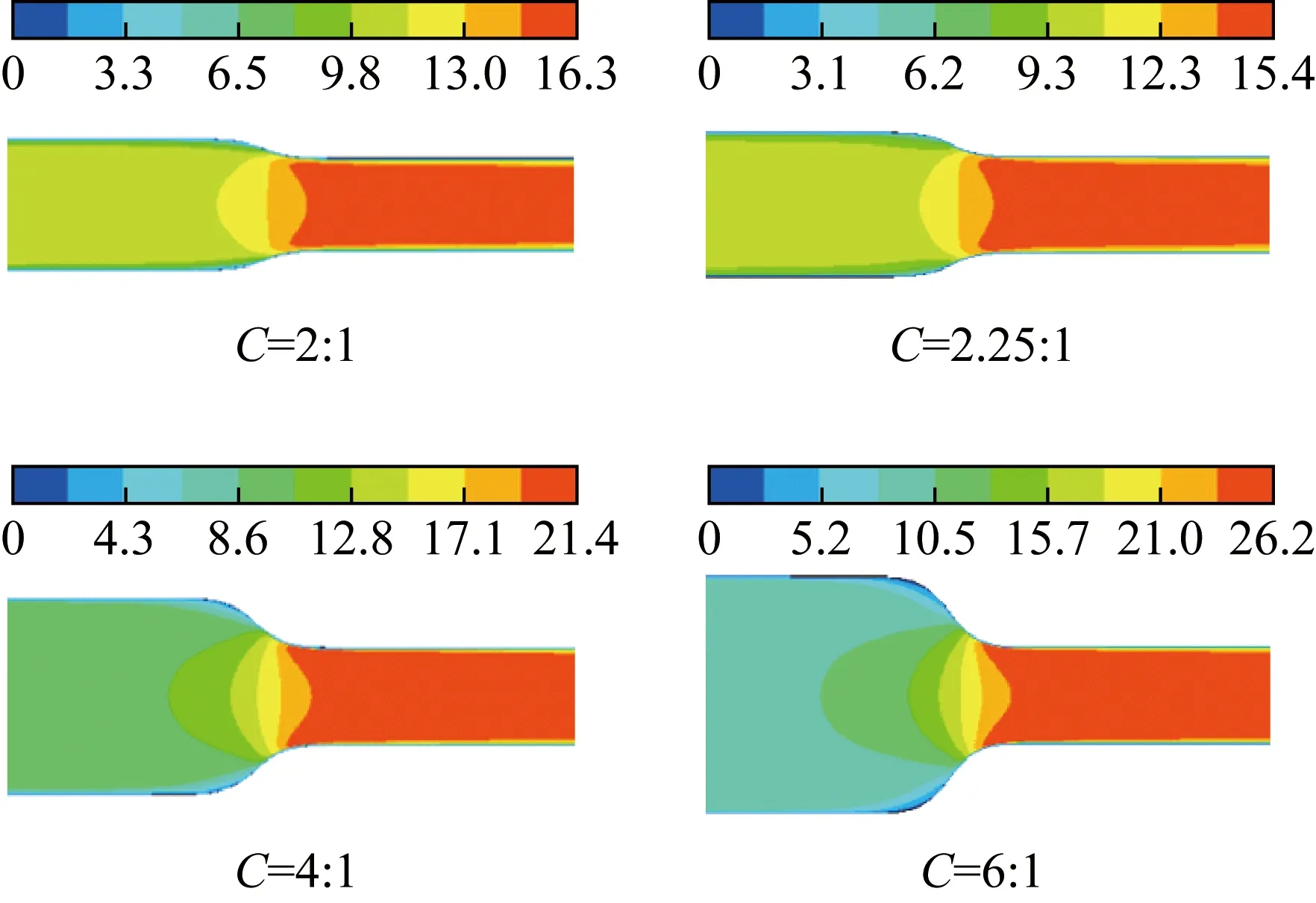
图3 不同收缩比的速度分布云图Fig.3 Velocity distribution clouds with different shrinkage ratios

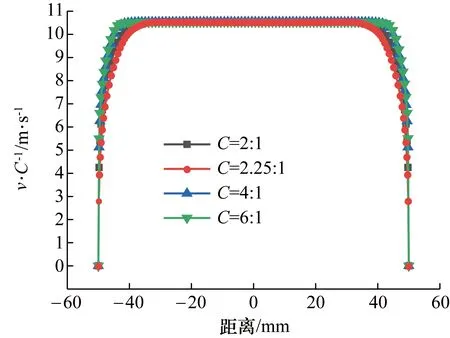
图4 不同收缩比的速度分布曲线Fig.4 Velocity distribution curves of different shrinkage ratios

为了更直观地表现收缩流场的差异,对各流场进行定量分析。在整个管道截面均匀取100个流速点,计算各流场的边界层厚度,核心区均匀性等参数,如表1所示。

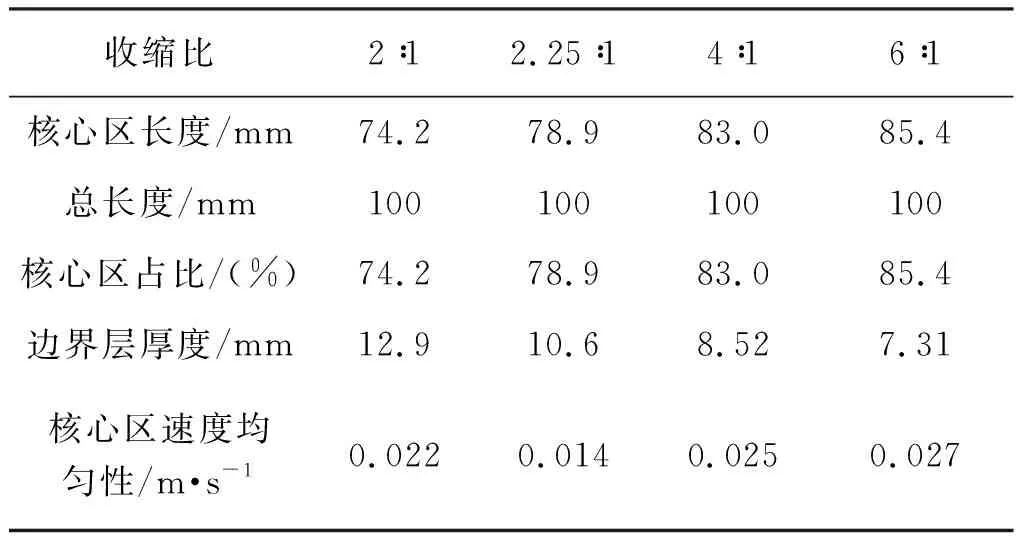
表1 不同收缩比的出口流场特征Tab.1 The characteristics of the outlet flow field with different shrinkage ratios

由表1可知,随着收缩比的增大,流场的核心区长度从74.2 mm增大至85.4 mm,边界层厚度由12.9 mm减少至7.31 mm,核心区域的速度均匀性保持在0.02 m/s左右。从流场均匀性角度分析,4种收缩结构均符合气体超声流量计测量要求。从边界层厚度[14]来看,边界层厚度决定了气体超声传感器的侵入长度,而气体超声流量计的测量误差会随着侵入长度的增大而增加。但收缩比过大会造成较大的压损,甚至可能形成漩涡等不利于测量的流动状态。由表1可知,当收缩比从2增加至6,边界层厚度最多只减少5.6 mm,影响较为有限。综合这些因素,本文采用了工程中较为常用的DN150～DN100(收缩比为2.25:1)的渐缩管,实现实验收缩流场的构造。

3.2 传感器安装长度确定

为了确定传感器的安装长度,还需确定流速与边界层厚度的关系,选取收缩比2.25:1的仿真模型,设置不同的初始速度,其它条件不变,得到数值如表2所示(表2中流速点为超声测量区域的平均流速)。

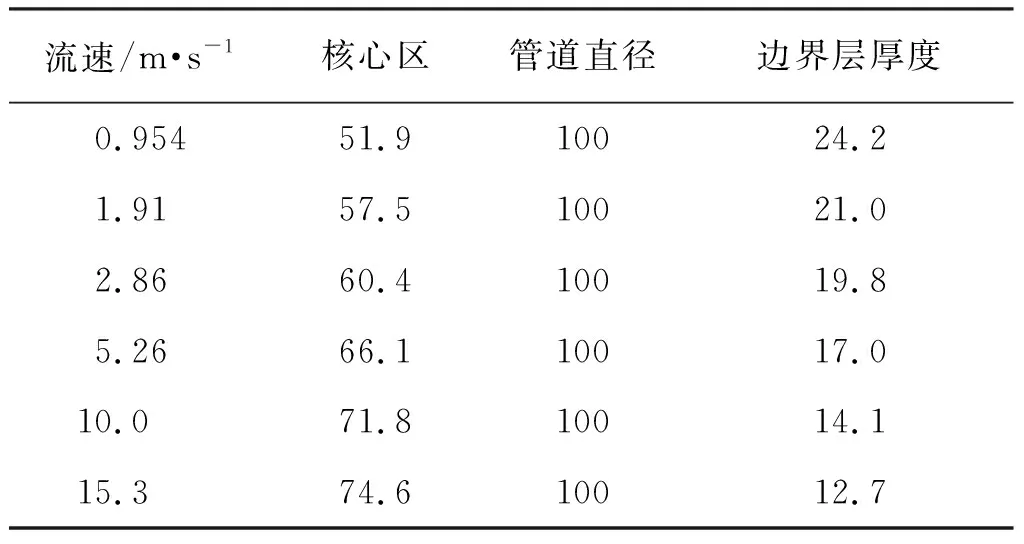
表2 收缩流场在不同流速下的边界层厚度Tab.2 Boundary layer thickness of shrinking flow field at different speeds mm

由表2可知,当流速从0.964 m/s增加至 15.3 m/s时,边界层厚度从24.2 mm减少至12.7 mm。考虑到气体超声传感器本身的长度(有效长度仅21 mm)以及侵入长度过长会大幅增加测量误差,因此在速度点5.25 m/s的边界层厚度作为传感器倾入长度,即将传感器信号发射、接收端内侵17 mm。

3.3 收缩修正系数

参考传统超声计流量计算方式,可以推算出基于收缩流动的流速修正模型。设收缩修正系数K′为管道截面平均速度与核心区平均速度的比值。通过式(6)可将气体超声传感器所测流速转化为管道截面平均速度:

(6)

但是流场流速分布影响因素较为复杂,并没有适合的经验公式能很好的表征出其流速分布,无法通过数值积分的方式求出收缩修正系数K′。因此利用数值模拟的方式,对不同速度点下的收缩流场进行分析,从而求出对应的K′值。提取出不同流速点下流场的关键信息如表3所示。

表3 收缩修正系数及相关参数Tab.3 Shrinkage correction factor and related parameters

为了更为直观地表现收缩修正系数与流速的关系,绘制如图5所示收缩修正系数随速度变化的曲线,发现当流速从0.954 m/s增加至15.3 m/s时,收缩系数由0.859增长至0.927。对其进行曲线拟合发现其曲线发展态势符合对数分布曲线,且与其拟合后的曲线一致。具体关系式为:y=0.024 4 ln(x)+0.859 9,利用其关系式,仅需测得管道内流速的值即可推出对应的收缩修正系数。

图5 收缩修正系数随速度变化曲线及拟合曲线Fig.5 The change curve and fitting curve of shrinkage correction coefficient with speed

4 流动测量模型实验验证

为了验证在收缩流动下低声道数气体超声流量计的测量准确度水平,需要通过实流实验进行具体的数值分析。

1) 建立更高标准的气体流量标准装置,提供稳定的气源,并以其流量值作为标准值对气体超声流量计测量准确度水平进行评价。

2) 加工与仿真模型相同的管道结构,完成基于收缩流动的气体超声流量测量模型的管道安装;保持其他条件不变,设定传统气体超声测量模型作为对照组。

3) 在相同条件下,对2种测量模型下不同声道数的流量测量准确度水平进行对比,并在此基础上对造成2种测量准确度差异的因素进行分析。

4.1 实验平台

实验在负压法流量标准装置上进行。该装置采用开路布置的方式,主要由真空泵组、气体超声实验测量段、音速喷嘴等组成,如图6所示。常压空气由真空泵组驱动产生压力差,形成流动气体,压力差保证了音速喷嘴下游的真空度;罗茨真空泵入口设置球阀及前置电动针阀。通过调节球阀开闭与电动针阀开度,可以粗略实现实验段流速的调整与控制。为了降低泵的流量脉动以及实现初始速度的精细化调控,设置1个音速喷嘴组,包括6支不同喉径的音速喷嘴,通过组合不同音速喷嘴,实现实验管路中流速和流量的精细调控。负压法流量标准装置测量不确定度为0.134%[15],最大测量流量为600 m3/h。

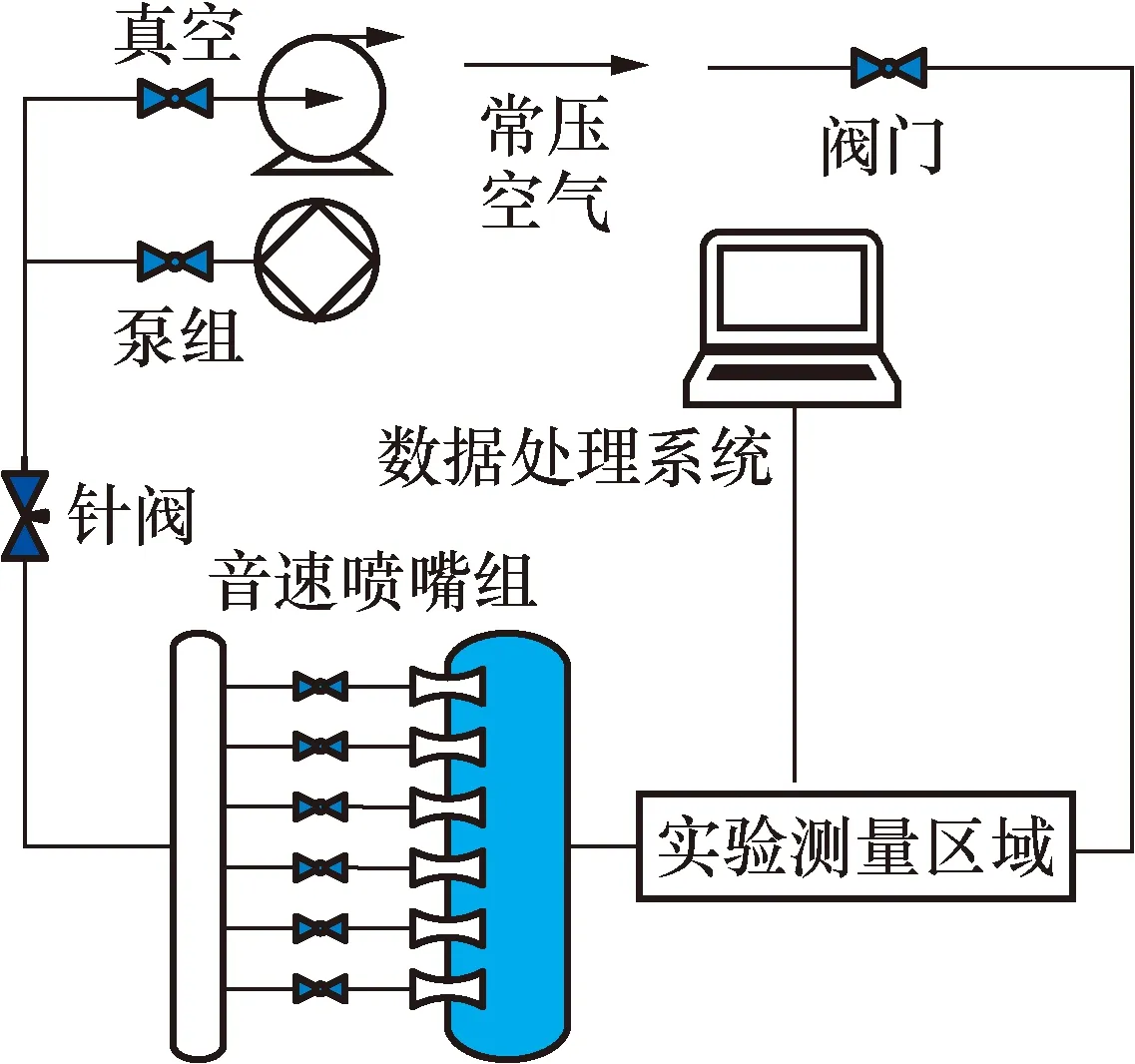
图6 负压法气体流量标准装置构成示意图Fig.6 Schematic diagram of the structure of a gas flow standard device for negative pressure method

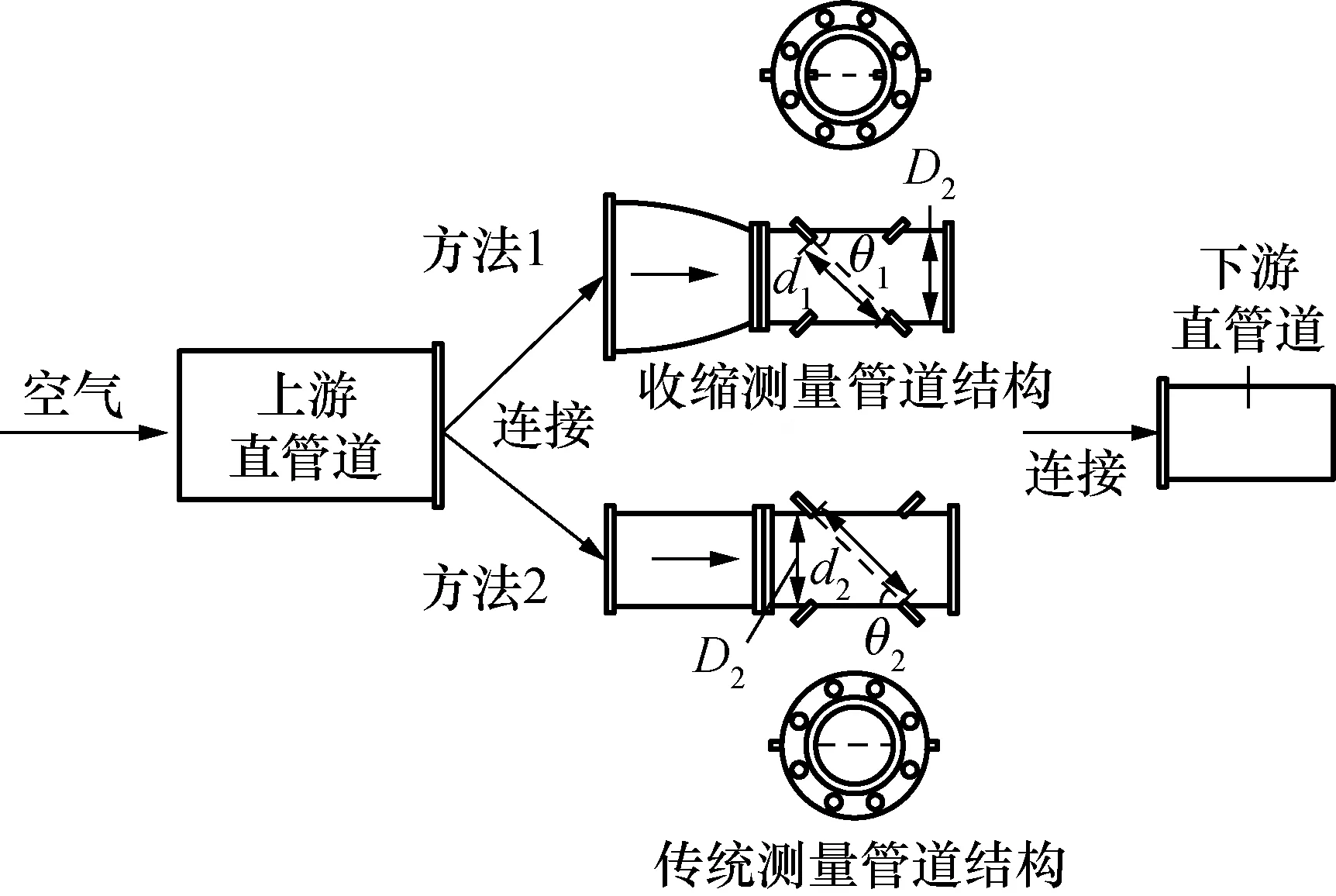
图7 收缩模型和等径模型2种实验测量管道结构Fig.7 Two types of experimental measurement pipeline structures: shrinkage model and equal-diameter model

实验测量区域分3部分,分别为上游直管道、超声流量测量管道、下游直管段。安装方式如图7所示。上游直管段长度为600 mm,直径随下游管道直管段直径而变化,使其保持等径连接;下游直管段长度超过700 mm,可避免下游管道过短引起的回流对上游流动过程的影响;超声流量测量管道分别设置收缩测量管道结构与等径测量管道结构，以验证基于收缩流动的气体超声流量计流量测量准确度水平是否符合要求。具体参数差异如表4所示。

表4 收缩模型和等径模型具体参数Tab.4 Specific parameters of shrinkage model and equal diameter model

图7所示均为双声道安装结构,双声道测量数据可直接由气体超声流量计测量得到;对于单声道可取其中一对探头所测数据作为单声道气体超声流量计测量值。

4.2 实验方案

按图6、图7要求安装测量管道,检查管道气密性与标准装置状态后开始进行实验。图8为实验安装现场管道结构图。开启真空泵组,使管道内气体流动。通过开启对应速度点的球阀,构造不同的流速,开启超声流量计,使其进入工作状态,读取并记录所测流速值,其具体实验参数如表5所示。

图8 实验安装图Fig.8 Experimental installation diagram Flow velocity sectional drawing

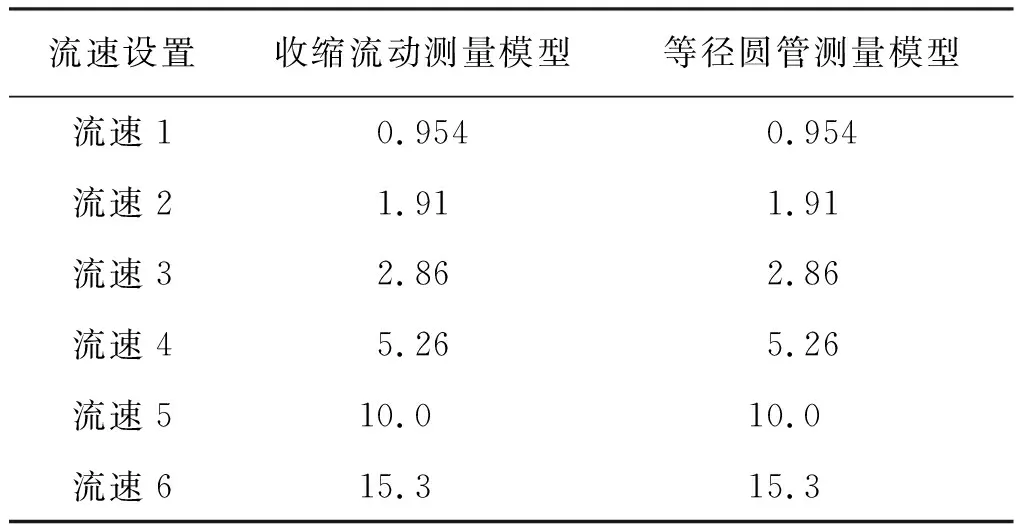
表5 实验参数Tab.5 Experimental parameter m/s

4.3 流量测量准确度

为了验证收缩流动测量模型是否能在降低声道数的情况下依旧保证流量测量准确度水平,分别对2种模型的单、双声道进行流量测量误差计算。由理论计算与数值模拟的结果，可得如表6所示的2种测量模型的流速修正系数。引入温度、压力、流量计系数[16]等参量对结果进行修正:

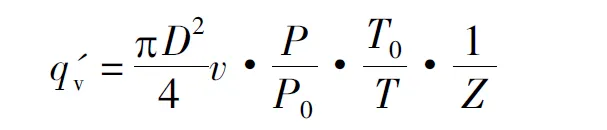
(7)

(8)

(9)

式中P0、P分别为标准状态和实际状态下的压力参数;T0、T分别为标准和实际状态下的温度值;Z为气体的压缩系数,由于采用的式负压法测量,被测管道与大气流通,因此可视为Z=1;F为流量计系数;qs、qh分别为标准体积流量和流量计显示流量;q为修正后的流量值。

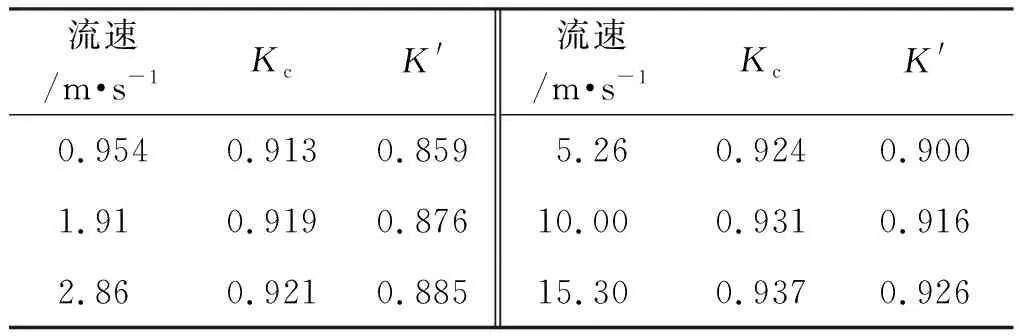
表6 流速修正系数Tab.6 Velocity correction factor

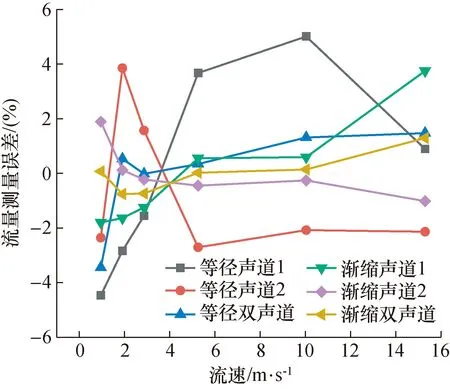
图9 流量测量误差对比Fig.9 Flow measurement error comparison

将修正后的流量q代入流量测量误差计算公式δ=(q-qs)/qs可得如图9所示结果。从图9可以看出,等径圆管测量模型的单声道测量误差较大,增加声道数可以有效的降低测量误差。而对于收缩流动测量模型来说,单声道测量误差相对较小,且通过增加声道数,对测量误差的减小较为有限,这是因为渐缩管控制下的流场为对称、均匀的高品质流场,对称安装的2个声道所测量的流速几近相同。同时将单声道收缩流动测量误差与双声道等径圆管测量误差相比,两者的测量误差较为相近。

4.4 测量准确度影响因素分析

收缩流动下的超声流量测量准确度水平明显优于传统超声流量计,为了了解存在差异的具体原因,对影响两者测量准确度的因素进行简要分析。已知影响其测量准确度的因素有管道直径、声道长度、速度测量重复性、传播时间等。但2种测量模型的被测管道、二次仪表的物理参数均相同,且双声道的积分余式的数值很小,对总体的测量准确度影响很小,可以忽略。则其测量准确度水平的差异主要来源为不同流场条件带来的流速测量的差异。因此对2种测量模型的流速测量重复性进行分析。通过式(10)计算流速的重复性,所得结果由表7、表8所示。

(10)

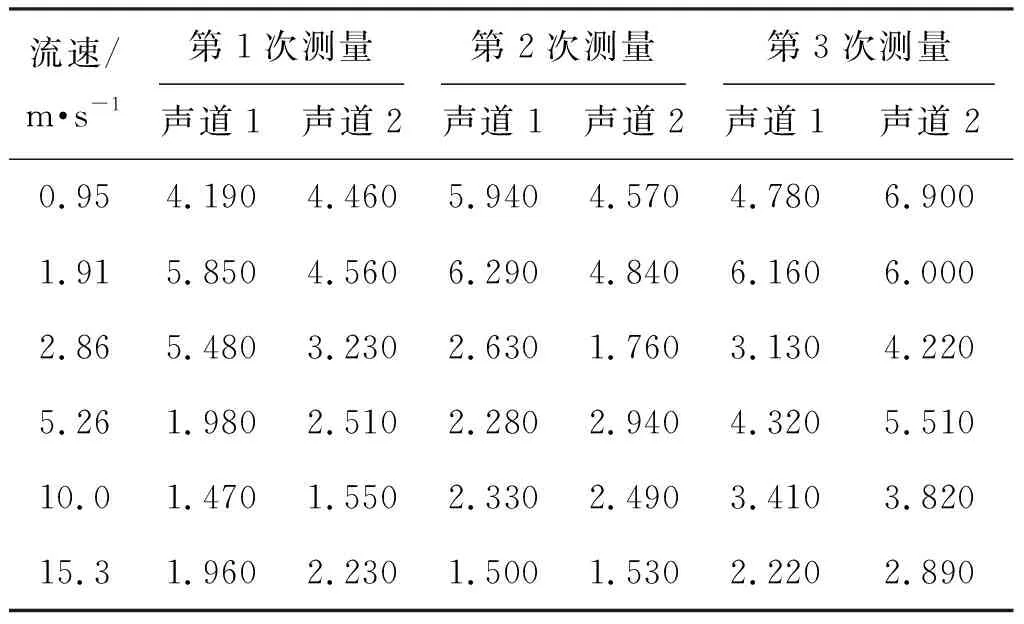
表7 等径圆管流速测量重复性Tab.7 Repeatability of flow velocity measurement for equal diameter round pipes (%)

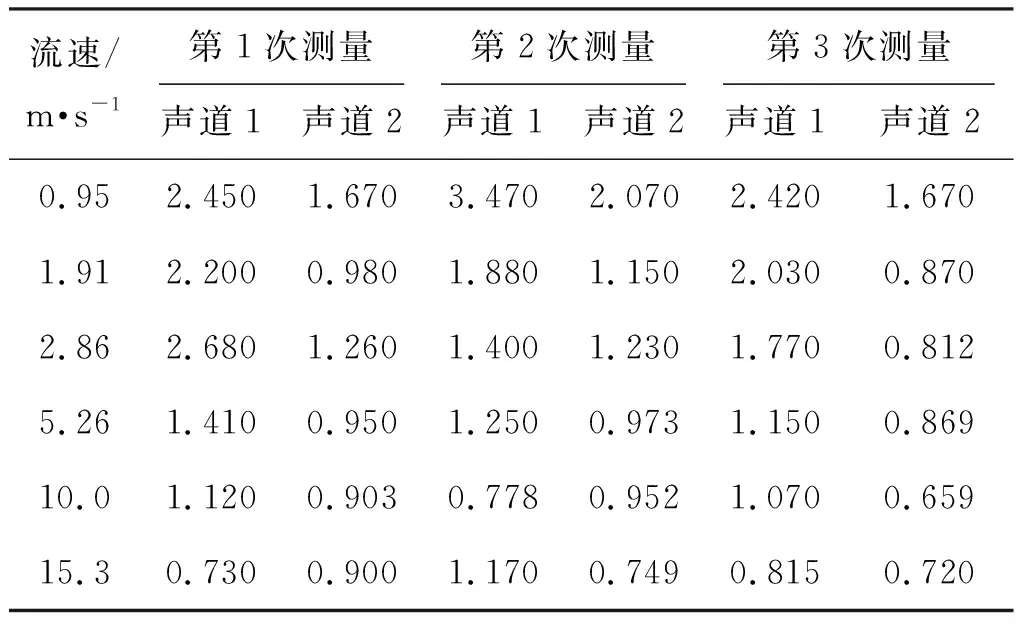
表8 收缩流动流速测量重复性Tab.8 Reproducibility of systolic flow velocity measurement (%)

依次筛选出每个流速度重复性最大的数值,并汇总成折线图,趋势如图10所示。由图10可知,对于等径圆管测量模型来说,随着流速的增大,测量重复性降低。结合其测量模型可知,随着流速的增大,边界层逐渐变薄后使边界层占整个管道截面的比重下降,边界层对测量的干扰程度下降,则流速波动越来越小,重复性越来越好，这时气体超声传感器所处边界层区域的比重与测量的准确度成反比。而对于收缩流动测量模型来说,当流速为0.95～5.25 m/s时,重复性随着流速的增大而减小。在流速为5.25～15.30 m/s时,流速重复性基本上保持不变。结合收缩流动测量模型的传感器安装方式可知,当流速低于5.25 m/s时,边界层厚度大于传感器侵入长度,此时信号发射、接收端处于边界层处,流速波动性较大,重复性较差。

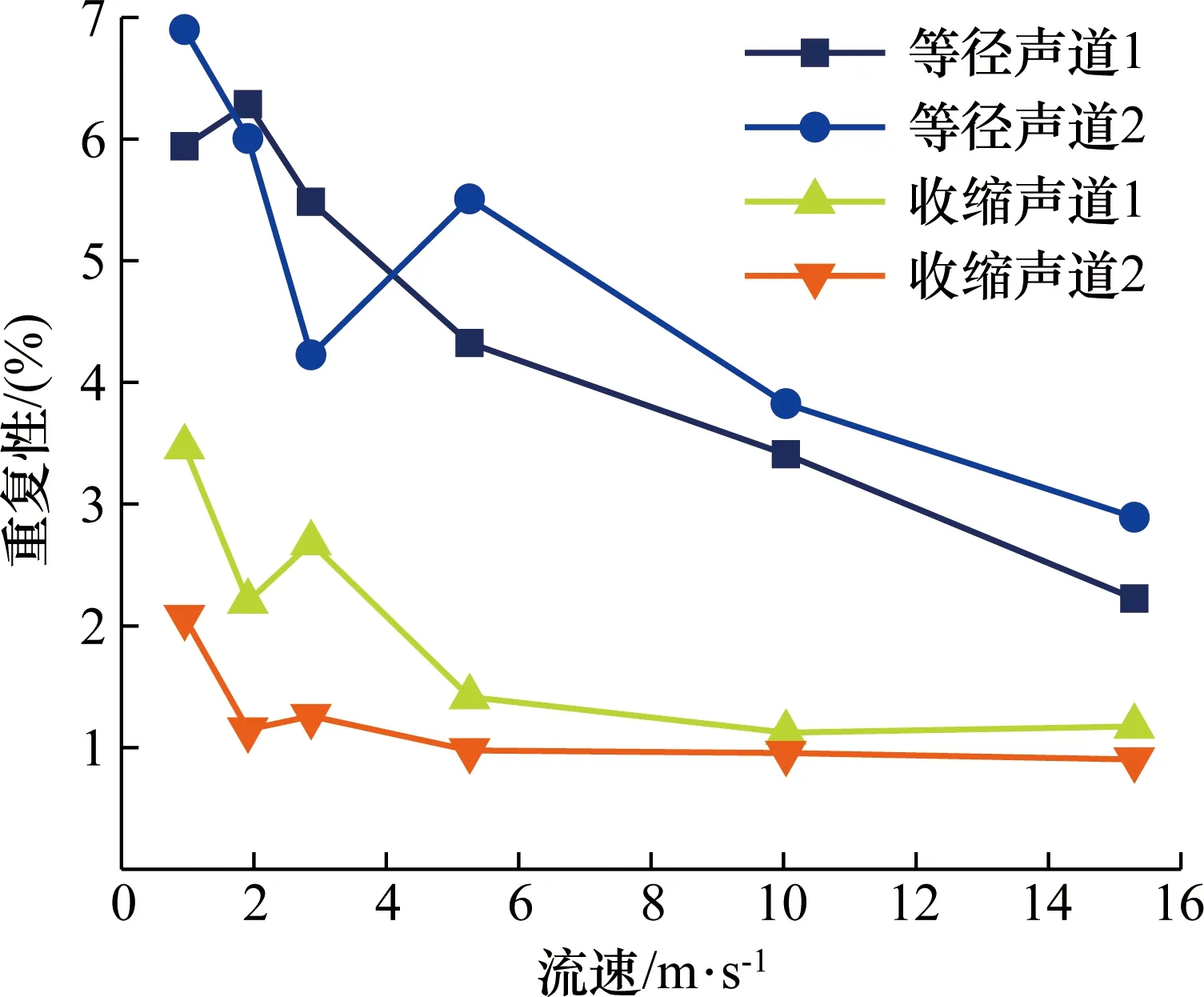
图10 流速测量重复性Fig.10 Repeatability of flow rate measurement

随着流速的增大,边界层变薄,测量重复性变好。当速度高于5.25 m/s时,气体超声传感器信号发射、接收端正处于流场均匀稳定的核心区域,随着速度的增大,边界层是否变薄对流速测量结果无影响。由实验结果可知:

1) 2种测量模型的测量准确度差异来源为气体超声传感器在不同流场条件下的流速测量能力的差异,气体超声传感器在收缩流场中的测量稳定性更高,测量性能更好。

2) 在收缩流场中,传感器测量区域的不同也会引起测量准确性的差异,当超声传感器底端处于边界层区域时测量能力较差,且其测量准确性随着边界层的减少而增加;当超声传感器底端处于流场核心区域时测量能力较高,其测量准确性与边界层大小无关。

5 总 结

为了验证所提出的渐缩管配比超声传感器核心区测量的测量模型是否能起到提升流量测量准确度的目的,对不同收缩比下收缩流场的流动状态进行了数值模拟计算,通过实验比较了收缩流动测量模型与等径圆管测量模型测量结果的差异,结合数值模拟计算与实验的相关结论,总结如下:

1) 渐缩管对流场具有良好的控制作用,所控制下的流场流速分布对称,其核心区速度均匀性较高。随着收缩比的增大,速度边界层变薄,相对湍流强度降低,但其核心区速度均匀性变化不大。

2) 收缩流动条件下的单声道气体超声流量计准确度水平显著优于传统单声道气体超声流量计,且与传统双声道气体超声流量计的准确度水平相当。

3) 2种测量模型的测量准确度差异来源为气体超声传感器在不同流场条件下的流速测量能力的差异,气体超声传感器在收缩流场中的测量稳定性更高,测量性能更好。