伺服电机转子位置检测的误差分析与补偿

张天恒, 童 鹏, 杨继森

(重庆理工大学 机械检测技术与装备教育部工程研究中心,重庆 400054)

1 引 言

在智能制造中,自动化程度要求越来越高,电机在农业、工业、国防等领域都得到广泛应用,在极端和特殊条件下,对温度、体积等有特殊要求的应用现场促使研发出新型电机,如无刷直流电机、开关磁阻电机、交流伺服电机等。转子位置的高可靠性检测才能保证这些新型电机稳定可靠高效运行。

目前转子位置检测有3类：无位置传感器、准无位置传感器和位置传感器检测技术[1～4]。为了提高电机转子位置检测的可靠性,在工业领域普遍采用位移传感器测量转子位置,但是该类传感器成本高、体积大,附加的机械结构也会影响电机运动性能,所以它们在工程应用过程中受到了一定程度的限制。

近年来,一些研究人员将隧道磁阻(tunnel magnetoresistance,TMR)用于角位移的测量,文献[5]将敏感测头采用TMR设计,虽然以独立的编码器测转子的角度,但是只能是外置传感器,且采用CORDIC解算方法,存在较大的输出角度误差；文献[6,7]中磁性旋转编码器同样是外置的传感器,不同之处是误差补偿的方式不同,文献[6]介绍了一种倾斜相角法的谐波滤波模型,虽然方法简单,主要是消除误差中的3次谐波成分；文献[7]运用径向基神经网络的误差补偿,需要采集大量的样本数据。

针对以上问题,本文提出了一种将TMR和时栅技术相结合。将安装TMR传感单元的电路板嵌入在电机端盖上,检测电机运动时的磁场的变化。当TMR元件检测到变化的磁场的时候,TMR元件输出与磁场同频率变化的电压信号,该电压信号就代表转子的位置信息。利用时栅技术,用时间量来实现转子位置的测量,摒弃了精密空间刻线就能实现位移的精密测量[8,9]。该方法将传感部件嵌入在电机端盖上使转子自带位置检测功能,既有效地利用了电机的无用空间,又避免由于电机轴系与传感器轴系进行机械连接所带来的误差。同时采用误差补偿,提高了检测单元的测量精度,成为实现电机转子位置测量的一种新方法。

2 嵌入式位置测量原理

TMR传感单元的设计基于自旋电子学。TMR隧道磁阻效应使传感器电阻随两铁磁层磁化方向夹角变化而呈正弦或余弦关系变化。TMR传感单元工作原理如图1所示,以一对TMR传感单元为例进行原理阐述,施加时间正交的激励信号给空间正交放置的一对TMR传感单元(TMRa和TMRb),其原理如图1所示。

Vain=Avsin (ωvt+θv)

(1)

Vbin=Avcos (ωvt+θv)

(2)

式中：Vain、Vbin分别表示TMR传感单元a和b的输入电压；ωv表示输入信号的角频率；θv表示输入信号的初相位。

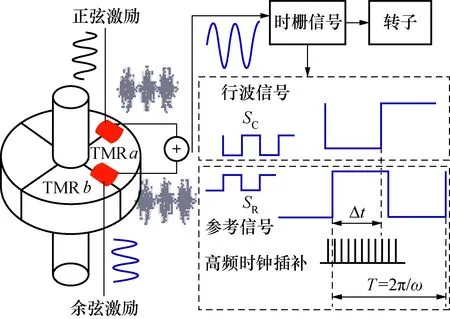
图1 电机转子位置嵌入式测量原理Fig.1 Embedded measurement principle of motor rotor position

电机旋转的时候会产生交变磁场,TMR检测单元所在位置的磁场发生周期性变化如式(3)、式(4)所示：

Ha=Ahcos (ωht+θh)

(3)

Hb=Ahsin (ωht+θh)

(4)

式中：Ha、Hb分别表示TMR传感单元在a和b位置的磁场电压；ωh表示磁场信号的角频率；θh表示磁场信号的初相位。TMR传感单元感应交变磁场,并分别输出一路同频同幅值相位互差90°的驻波,两路驻波叠加后就得到转子位置的行波信号式(5),式(7)可以化简为式(6)[6]。

Vt=Vaout+Vbout

=SAvAhsin (ωvt+θv) cos (ωht+θh)+

SAvAhcos (ωvt+θv) sin (ωht+θh)

=SAvAhsin [(ωv+ωh)t+(θv+θh)]

(5)

Vt=Atsin (ωt+θt)

(6)

式中：Vt表示合成行波信号的电压；At表示行波信号的幅值；ω表示行波信号的频率；θ表示行波信号的相位。通过对行波信号和参考信号之间的相位差进行高频时钟脉冲插补计数,根据空间和时间的对应关系,角位移和时间之间存在式(7)的关系,实现转子角位移的测量,从而摆脱了长期以来位移测量依赖空间的高精度刻线。

(7)

式中：T表示信号周期；θ表示角位移；Z表示空间节距；V是行波磁场的速度；Pi插补脉冲数。

3 误差分析

在测量系统中存在许多误差因素,根据转子位置测量系统的原理,其主要误差来源包括传感器安装误差、信号处理误差等。

3.1 安装误差

安装误差主要由每对TMR传感单元空间不正交如图2(a)、每对TMR传感单元不在同一水平面上如图2(c)、转子轴和TMR的PCB板不同心如图2(d)的误差组成。对角度传感器而言,偏心都会带来一次谐波误差,同样的若安装导致每对TMR传感单元不同心如图2(b),感应的磁场一周之内不均匀,引起一次谐波误差。若TMR传感单元安装不在同一水平面上,会导致TMR传感单元感应到的磁场信号在水平方向和竖直方向的磁场状态改变,沿水平方向的磁场状态变化表现为两者之间存在偏心,从而引起一次谐波误差。沿竖直方向的磁场状态变化等效于电气误差中的激励信号幅值不相等,下文将做具体分析。

TMR传感单元空间不正交如图2(a)所示。

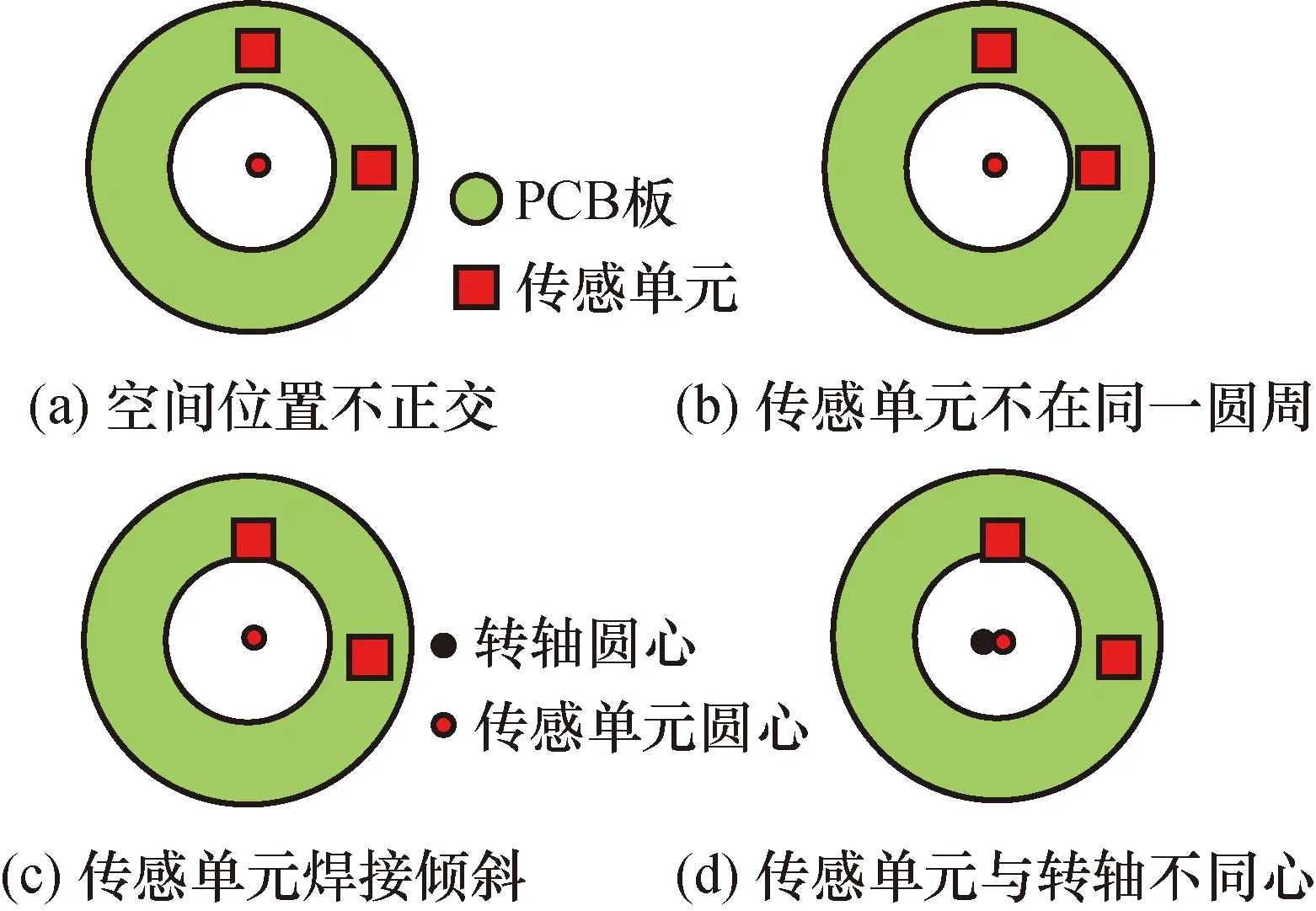
图2 传感单元装配误差 Fig.2 Assembly error of sensing unit

若TMR传感单元在位置a和b的空间位置不正交,如图3所示。则会引起TMR传感单元感应到的磁场信号不正交,如果TMR传感单元在位置a和b实际感应到的磁场信号为：

Va=Vmcos (ωht-φ)

(8)

Vb=Vmcosωht

(9)

图3 TMR芯片空间位置不正交Fig.3 TMR chip spatial position is not orthogonal

用相量来表示式(8)、式(9),得到式：

(10)

(11)

式(10)、式(11)与时间正交的激励信号相乘,产生两路驻波,两路驻波叠加后形成复数形式的行波表达式：

(12)

由于φ很小,根据复数的性质和欧拉公式,式(12)可以转化为：

(13)

式(13)用相量图4来表示。从图4看出,每对TMR传感单元空间位置不正交,产生相位差的误差表达式为：

(14)

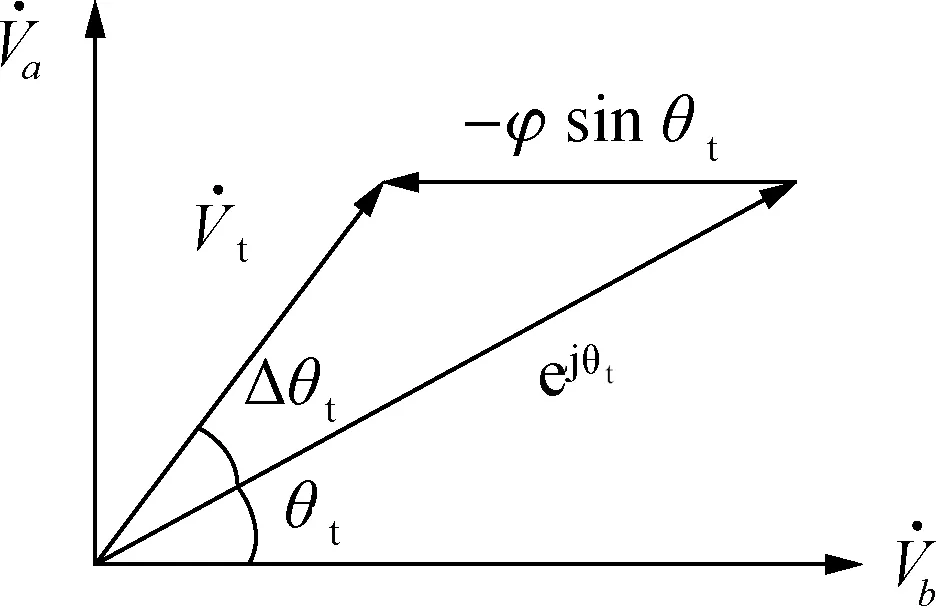
图4 TMR空间位置不正交误差相量图Fig.4 Non orthogonal error of TMR spatial position

由式(14)可知,TMR传感单元空间位置不正交会导致常值误差和二次谐波误差的产生。

3.2 电气误差

电气误差是指两路激励信号的幅值、相位等物理量不相等和差分放大器存在零点漂移时,导致的测量误差。

当两路激励信号在时间上不正交时,导致TMR传感单元之间存在相位差,与上面分析的TMR传感单元空间位置不正交类似,同样会引起常值误差和二次谐波误差。

不管是激励信号和感应信号,如果幅值不完全相等,对于测量结果的影响是一样的。以两路激励信号的幅值不相等为例,来分析造成的测量误差。假设两路激励信号之间的幅值相差δ,两路激励信号的复数表达式为式(15)、式(16)：

(15)

(16)

同样的方式得到行波形式的表达式为：

(17)

式(17)的相量图如图5所示。从图5看出,信号幅值不相等而导致的测量误差为式(18)：

(18)

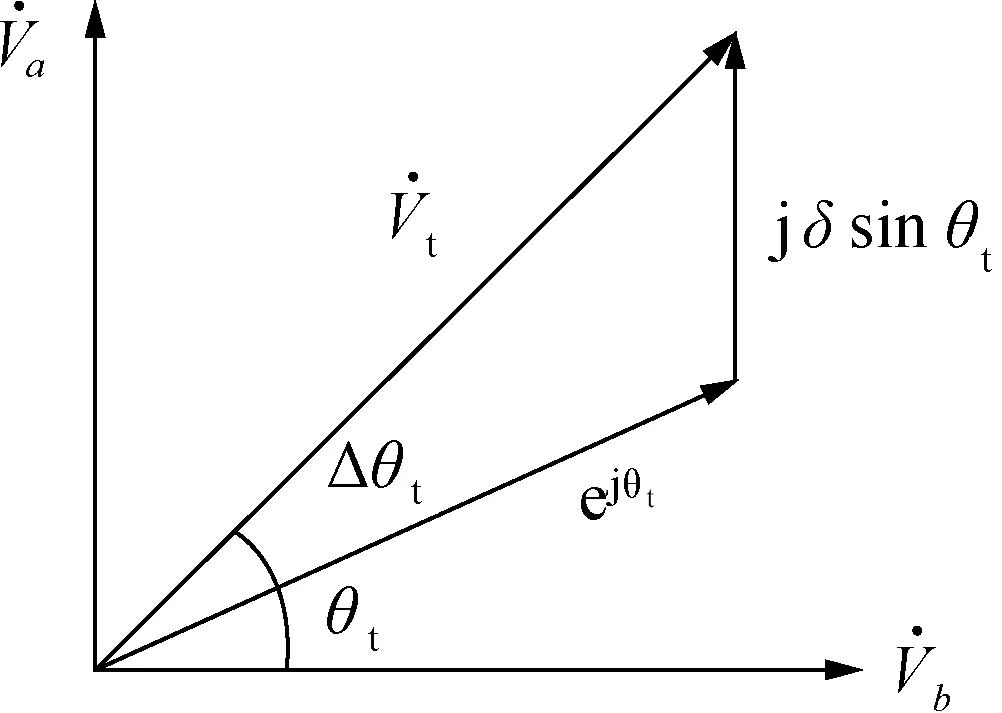
图5 两路激励信号幅值不等的误差相量图Fig.5 Error phasor diagram of two excitation signals with different amplitudes

由式(18)可知,TMR信号幅值不等就会产生一个二次正弦误差。

另外电机内部磁场环境复杂,电磁干扰和电磁噪声也会导致测量准确度下降。例如电机的电磁噪声是由于齿槽效应、磁路的磁饱和效应等引起的电机气隙磁场畸变引起的,气隙磁场畸变导致产生谐波频次为2次和3次谐波,而4次谐波成分来源于2、3次谐波成分的叠加[10]。电磁噪声随着电机转速的增加,噪声也随之增强,对测量的影响越来越大,甚至淹没有用信号。电磁噪声是由电机绕组中的电流谐波等引起的,电流谐波中包含5,7,11,13次谐波[11,12]。

4 软件补偿

4.1 ELM算法

2006年,Huang等提出了超限学习机(extreme learning machine,ELM)[13]智能学习理论,该理论突破了以前流行的前馈神经网络学习理论和方法,具有学习速度快、准确度高等优点。利用超限学习机理论对转子嵌入式位置检测的非线性误差模型进行训练和补偿,提高位置检测的精度。

由文献[14,15]可知,只要激励函数g(x)满足在任意实数区间上无限可微,就无需对wi和bi随机初始化进行调整,输出层也不需要偏置,输出权值βi通过正则化原则计算,就可逼近任意连续系统,几乎不需要学习。其网络结构如图6所示。

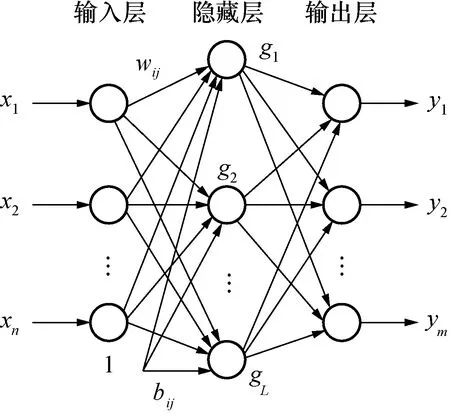
图6 ELM网络结构图Fig.6 Network structure diagram of ELM

假设隐含层神经元个数是L,训练集包含N个不同样本(Xi,Yi),其中输入Xi=[Xi1,Xi2,…,Xin]∈Rn,输出Yi=[Yi1,Yi2,…,Yim]∈Rm,若采用非线性激活函数g(x),来自同一连续系统的N个输入样本用零误差逼近,则神经网络的输出模型是：

(19)

式中：wi=(wi1,wi2,…,win)；

xj=(x1j,x2j,…，xnj)T。

4.2 TMR传感单元非线性误差模型训练

根据对TMR传感单元误差分析可知,实际的角度值和测量角度值之间存在单输入单输出的非线性关系,以传感器实际的角度值和测量角度值组成训练集,对输入与输出关系进行训练,建立误差模型,误差模型的网络结构如图7所示。

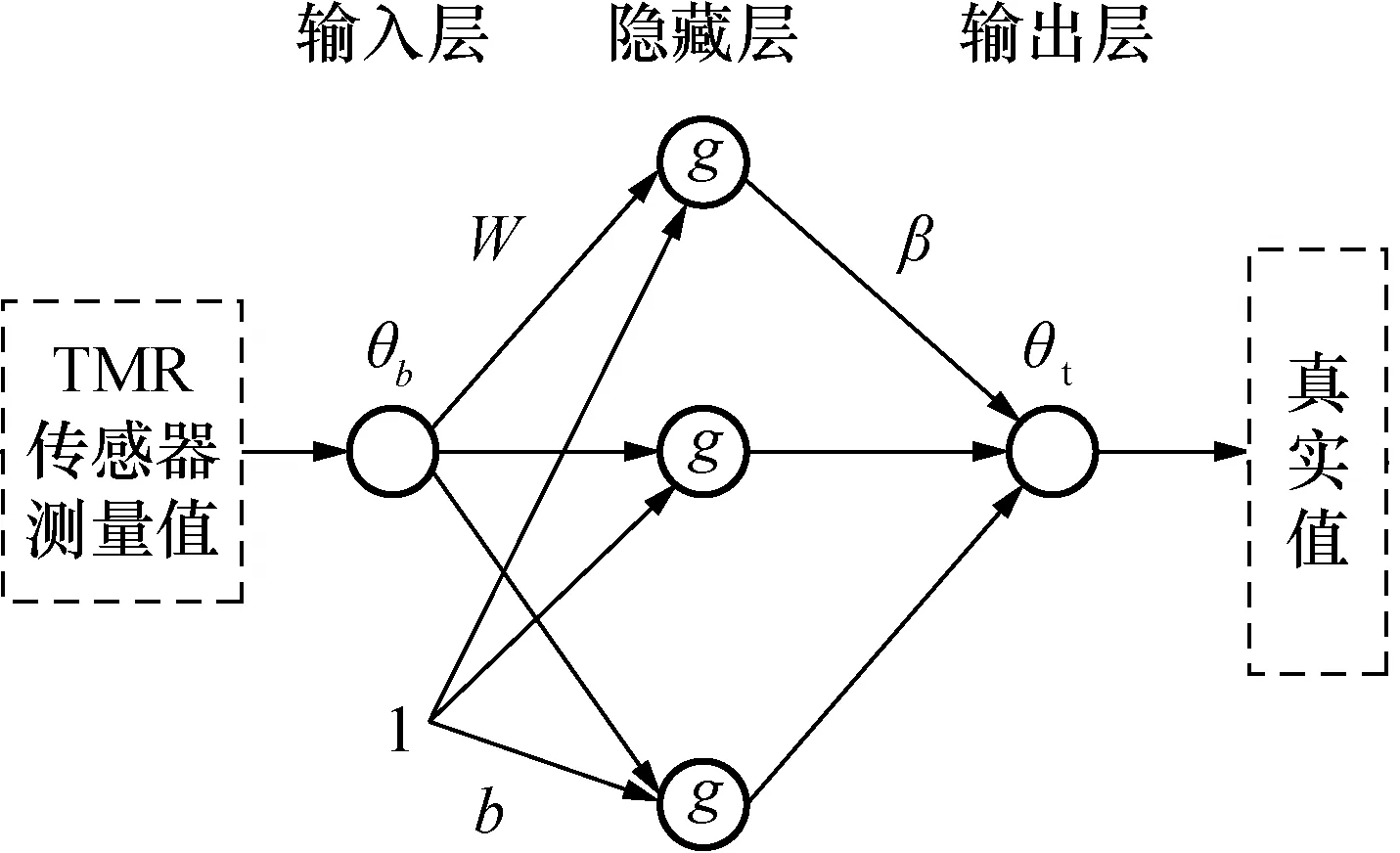
图7 TMR传感器的误差训练模型Fig.7 Error training model of the TMR sensor

ELM训练的目的是确定偏置b和权值w、β。 训练流程如下: 1) 隐藏层神经元数可根据经验设置,不妨设置隐藏层节点数L=12[16]。2) 系统随机产生输入偏置b和权值w,计算神经网络随机输出矩阵H。3) 根据式(21) 计算输出权值β。

βi=[βi1,βi2,…,βim]T，

Y=Hβ

(20)

随机输出矩阵：

(21)

式中：Y表示输出矩阵;H+为隐藏层输出矩阵的莫斯广义逆。

4.3 传感器误差补偿模型

通过ELM算法训练所得参数w、β与偏置b后,建立嵌入式TMR传感单元的误差模型,并利用该模型实现对转子位置的补偿,则补偿后的转子位置是：

θt=gβ(θbw+b)

(22)

式中：θb为补偿前TMR测量的角度值；θt为补偿后TMR测量的角度值。

5 实 验

5.1 测量系统实验台

加工设计了电机转子位置测量的实验平台。实验台主要由上位机、主控系统板、永磁同步伺服电机、传感器、PLC、交流电源等几部分组成,具体如图8所示。将装有TMR的PCB板(厚度0.8 mm)嵌入在电机端盖的无用空间中,既没破坏电机的结构又便于安装,不需要别的连接装置与空间来安装位置传感器,实现转子位置的测量。实验过程中,PLC控制电机运动,将正余弦激励信号(2 V， 4 kHz)通入一对TMR传感单元中,传感器会检测到电机转子的磁场变化,将输出的两路驻波信号叠加得到转子位置的行波信号,转子位置的行波信号经主控系统处理就可以计算出转子的位置。

图8 嵌入式位置检测实验平台 Fig.8 Embedded position detection experiment platform

5.2 误差模型标定和补偿

误差模型标定的目的就是确定式(22)中的各项系数。针对嵌入式TMR传感单元非线性误差的标定,选用精度为6′的光电编码器进行测试标定。将光电编码器安装在电机转轴上,在电机转速为2000 r/min的条件下,上位机同时采样电机转子位置与光电编码器的值。利用光电编码器测试标定得到的数据,通过傅里叶变换可计算得到线性拟合各参数的最优估计值。图9(a)为标定得到的补偿前的误差曲线,误差峰峰值为293.4′。将标定得到的数据应用数学方法进行前20次频谱分析,频谱图如图9(b)所示,从图9(b)可以看出其谐波成分相当复杂,但是前13次的谐波的幅值比较大,后面的幅值比较小,验证了误差分析的正确性。

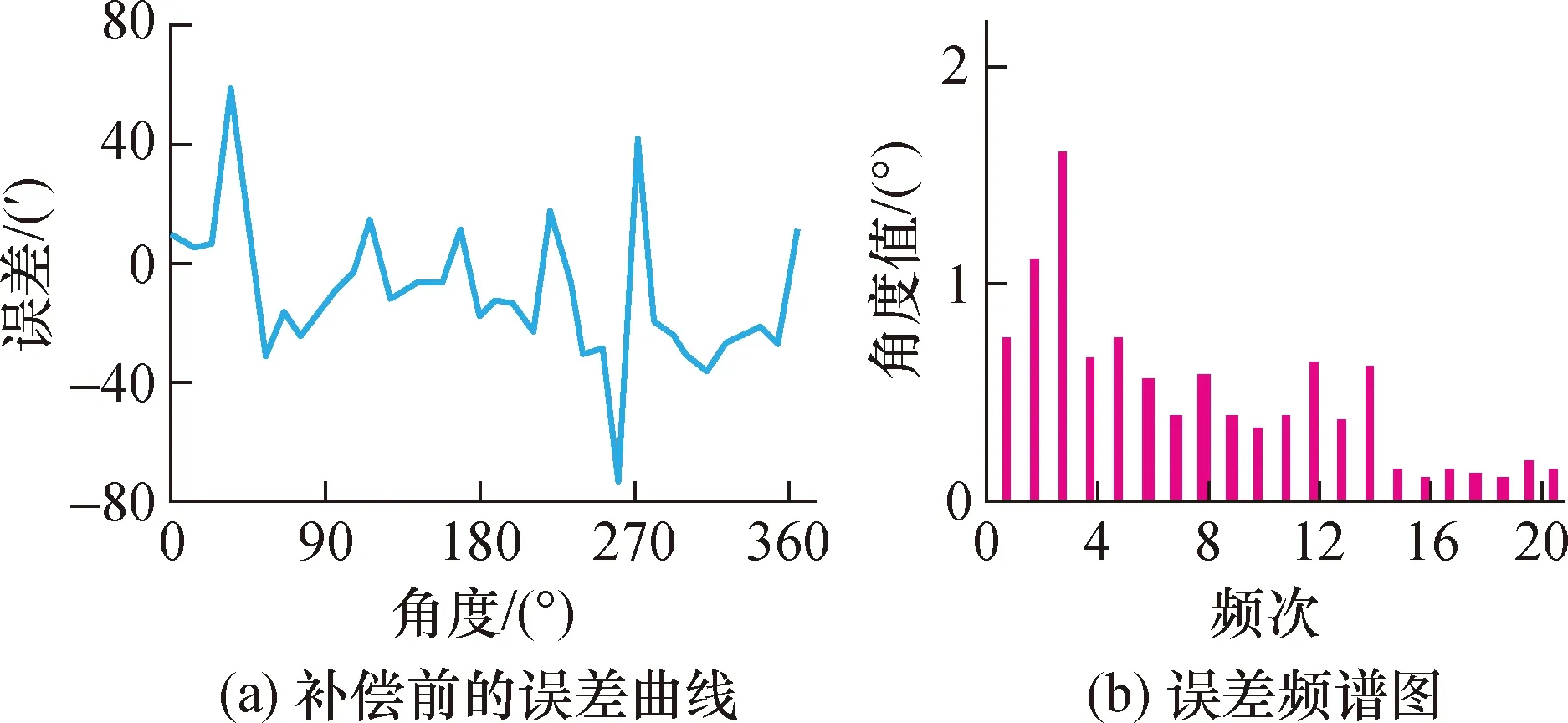
图9 转速为2000 r/min时的误差曲线与频谱Fig.9 Error curve and spectrogram at speed of 2000r/min

根据补偿模型计算出补偿参数,补偿参数如表1所示。将表1的补偿参数下载到主控系统板,同时为了验证ELM补偿方法的稳定性和有效性,在转速为2000 r/min 和500～5000 r/min的条件下进行测量,转速为2000 r/min匀速测量误差如图10所示：补偿前的误差峰值为4.64°,补偿后为0.315°,ELM的补偿模型有效地降低了误差。补偿后的精度接近于光电编码器的精度。

表1 补偿参数Tab.1 Compensation parameters

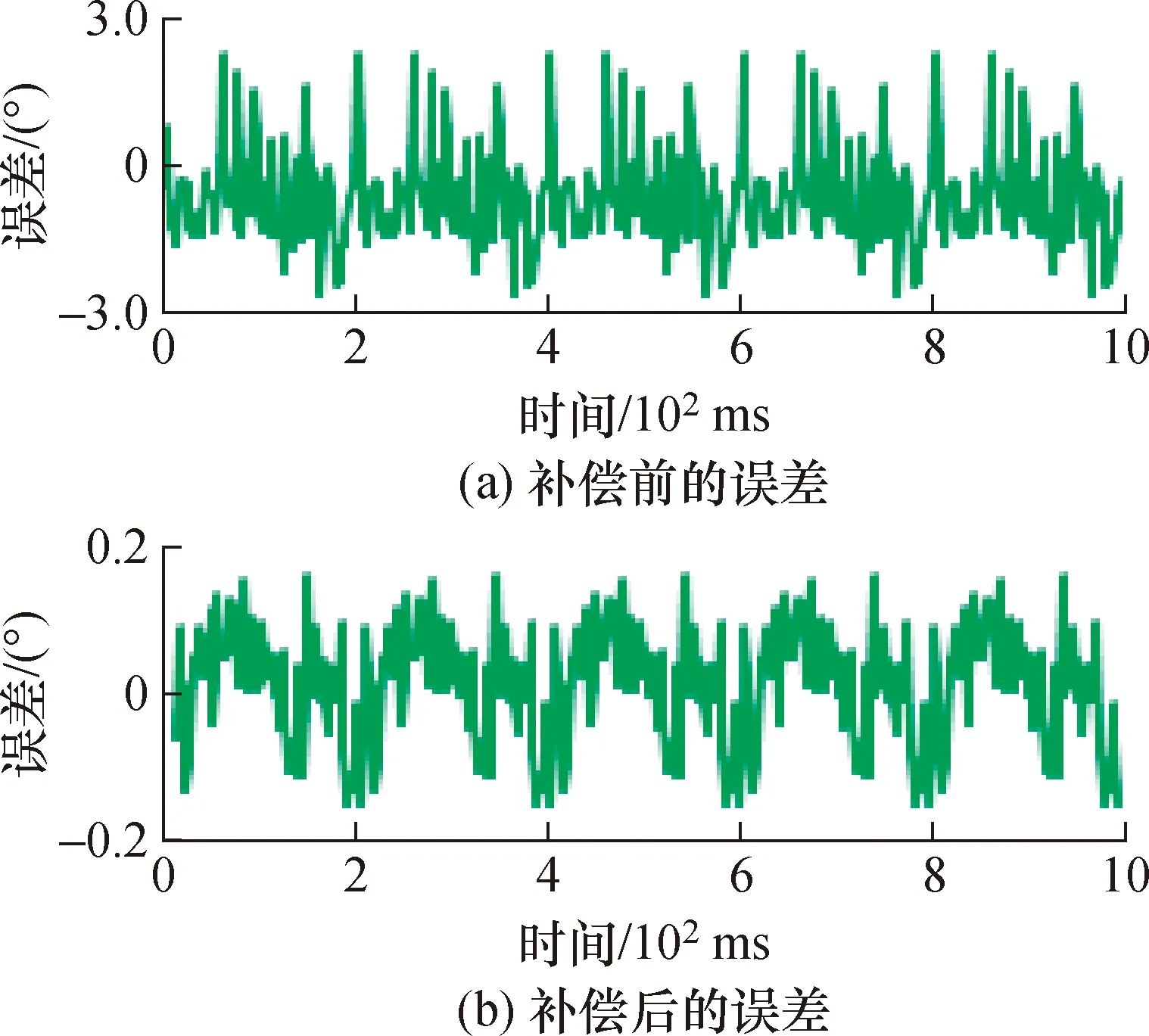
图10 2000 r/min匀速测量补偿前后误差Fig.10 Error before and after compensation for 2000 r/min constant speed measurement

转速为500～5000 r/min变速测量误差如图11,补偿前的误差峰值为7.326°,补偿后为0.767°。随着转速增大精度明显变差。一方面说明了动态测量的随机性,另一方面随着转速提高TMR传感单元自身采样的原始误差发生变化,在速度为2000 r/min的条件下求解出的参数已不能满足变速与高速的要求。

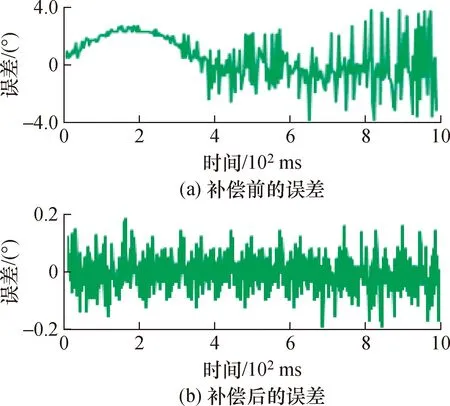
图11 500～5000 r/min变速旋转补偿前后测量误差 Fig.11 Error before and after compensation of 500～5000 r/min variable speed measurement

6 结 论

针对当前用于电机转子位置检测中的优缺点,采用TMR为传感元件和时栅技术相结合,阐述了嵌入式TMR测量方法,为电机转子位置检测技术研究提供了一种新的思路。

(1)将传感元件通过PCB板嵌入在电机前端盖上,缩小传感单元的体积、便于安装。

(2)为了降低原始误差,提出了基于超限学习机的误差补偿模型。在电机转速为2000 r/min和500～5000 r/min的时候,精度分别提升了约93.2%和89.5%。

(3)优化传感器的硬件电路,研究提高激励信号的频率和在变速运动下电机转子位置检测的精度。

(4)电机使用过程中,由于机械磨损等因素,误差模型并非一成不变,模型参数产生变化,这样将导致补偿效果变差,通过重新误差修正补偿或者研究一种智能自修正误差补偿方法。