质点与圆弧槽系统问题情境的有效设计与分析方略

江西 许冬保

无论是在高三总复习的综合检测，还是强基计划模拟测试中，质点与圆弧槽系统问题都频频出现。特别是在各地联考中，常作为压轴选择题出现。这类问题设计一般以“学习探索情境”为载体，重点考查学生“科学思维”学科素养中的模型建构、科学推理及科学论证等要素，以及“物理观念”中的运动与相互作用观念和能量观念等要素。下面通过实例，谈谈质点与圆弧槽系统问题情境的有效设计及其分析方略。

1 质点与圆弧槽系统问题情境的设计

在质点与圆弧槽系统中，质点、圆弧槽及质点和圆弧槽系统与系统外物体的相互作用，可以构成灵活多变的运动情境。命题设计主要有以下7种方式：

(1)对质点与圆弧槽系统平衡问题的分析；

(2)质点在固定圆弧槽中运动，探究质点的运动规律；

(3)质点在可动圆弧槽中运动，系统动量守恒及机械能守恒的判断；

(4)质点在可动圆弧槽中运动，探究质点及圆弧槽的运动(速度、位移等)规律；

(5)质点在可动圆弧槽中运动，探究质点运动的最大速度；

(6)质点在可动圆弧槽中运动，探究质点与圆弧槽的相互作用力；

(7)质点在可动圆弧槽中运动，探究质点与圆弧槽的运动周期。

2 问题情境的有效设计与分析

问题情境的有效设计，是在《中国高考评价体系》及《普通高中物理课程标准(2017版2020年修订)》(以下简称《课程标准》)视域下，所进行的相关分析。

2.1 质点与圆弧槽系统的平衡问题

【例1】(2022·临汾市第二次模拟考试)如图1，倾斜固定的长木板A上放置一个内壁光滑的半球形凹槽B，凹槽中放有小球C，整个装置处于静止状态。若缓慢减小长木板倾角θ，下列说法正确的有

图1

( )

A.小球对凹槽的压力逐渐增大

B.凹槽对长木板的压力逐渐增大

C.长木板受到凹槽的摩擦力逐渐减小

D.长木板对凹槽的作用力逐渐减小

A

B

C

D

【解析】设小球C及凹槽的质量分别为m、M，重力加速度为g。由于凹槽B内壁光滑，因此，小球C在凹槽中处于静止状态时，其所受重力与凹槽对其的支持力大小相等，方向相反。

设长木板所受凹槽的弹力及摩擦力分别为FN、Ff。由平衡条件有FN=(m+M)gcosθ，Ff=(m+M)gsinθ

当倾角θ缓慢减小时，FN不断增大，Ff不断减小；长木板对凹槽的作用力始终等于系统的重力。

综上，正确选项是BC。

【评述】该题情境设计符合上述考查方式中的命题设计(1)。缓慢减小长木板的倾角θ，小球与凹槽均处于平衡状态，涉及共点力的平衡条件、受力分析及力的合成与分解等知识内容。要求学生能依据隔离法及整体法分析问题。试题突出对“科学思维”学科素养中的模型建构、科学推理等要素的考查。

2.2 质点在固定圆弧槽中的运动问题

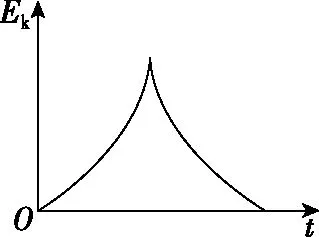
【例2】(2022·如皋市高三期末考试)如图2，一个小滑块从光滑固定的圆弧槽的A点由静止释放后，经最低点B运动到C点的过程中，小滑块的动能Ek随时间t的变化图像可能是

图2

( )

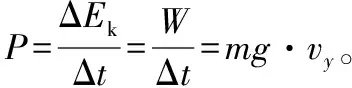
【评述】该题情境设计符合上述考查方式中的命题设计(2)要求。解答的关键是，将动能随时间变化的规律转化为重力做功功率随竖直方向分速度变化的规律。该题主要考查学生定性或半定量的分析能力与推理论证能力。

2.3 质点与圆弧槽的相互作用问题(定性)

【例3】如图2，在光滑的水平面上有一光滑半圆弧槽Q，最低点为B，A、C为半圆水平直径的端点。若让小滑块P沿槽的内壁从A点由静止下滑，则

( )

A.P不能到达Q右端的C点

B.P从A到B的过程中，Q向左运动；P从B到C的过程中，Q向右运动

C.P从A到C的过程中，Q一直向左运动；P到达C点的瞬间，Q的速度为零

D.P与Q组成的系统在水平方向上动量守恒

【解析】设P、Q的质量分别为m、M，作用后两者的共同速度为v。研究P、Q系统，由水平方向动量守恒有(m+M)v=0，解得v=0。由系统机械能守恒可知，P一定能到达Q右端的C点。

P从A到B的过程中，弹力对Q做正功，Q向左加速运动；P从B到C的过程中，弹力对Q做负功，Q向左减速运动；P速度减为0时，Q速度亦为0。综上，正确选项是CD。

【评述】该题情境设计符合上述考查方式中的命题设计(3)要求。考查动量守恒定律及机械能守恒定律成立的条件。在此基础上，进行定性或半定量的分析得到P相对Q做圆周运动，P相对地面构成椭圆摆模型。凸显理解能力及推理论证能力的考查。

2.4 质点与圆弧槽的相互作用问题(定量)

【例4】一质量为m的质点从置于光滑水平面上的、质量为M的光滑的、半径为R的弧形槽的顶端滑下，如图2所示，开始滑下时，m、M都处于静止状态，质点到达弧形槽最低点B时，求：

(1)质点和弧形槽的速度；

(2)弧形槽的运动的位移；

(3)质点对弧形槽的压力。

【解析】(1)设质点到达弧形槽最低点B时，质点和弧形槽的速度分别为v、V，取向右为正。m、M在水平方向上动量守恒，系统机械能守恒，则有mv+MV=0

V<0，则表明圆弧形槽在水平面上向左运动。

【评述】该题情境设计符合上述考查方式中的命题设计(3)、(4)、(6)。将质点与圆弧形槽整体作为研究对象进行分析，考查动量守恒定律、机械能守恒定律及牛顿运动定律的综合应用。要求有较强的应用数学处理物理问题的能力及推理论证能力。问题(2)类比人船模型来处理更方便。问题(3)中，向心加速度中的速度为相对速度。若用隔离法处理，则需要运用质点动力学理论求解。过程如下：

设FN为弧形槽对质点的作用力，沿水平向右为正方向，对质点、弧形槽分别用动量定理(只写水平方向的分量方程)和动能定理，建立如下方程。

式中drmM=drm-drM是质点对弧形槽的相对位移，drmM沿弧形槽的切线方向，任意时刻都有FN⊥drmM，FN·drmM=0。所得结果同上。

3 问题情境的设计误区

综上所述，在质点与圆弧槽系统中，质点沿圆弧槽运动涉及力学中的动量、能量以及力和运动关系等知识的综合应用。依照《中国高考评价体系》，试题设计应遵循基础性、综合性、应用性及创新性的原则。特别是在追求创新方面，可能由于考虑不慎而走向误区，这样就会影响试题的信度、效度等测量指标。

3.1 小滑块沿圆弧槽运动的表述优于小球沿圆弧槽运动的表述

考查一个质量为m、半径为R的小球，从倾角为θ的斜面上滚下来的情境。从动力学视角考虑，小球为刚体，以小球与斜面接触点为瞬心，由转动定律知

若从能量的视角来分析，需要考虑小球的转动动能。尽管小球半径较小，但用小物块或小滑块来替代小球是严谨、规范的。因此，在高考试题中，涉及物体沿斜面或曲面的运动时，研究对象常常用小物块或小滑块，而不用小球。

3.2 质点在槽最低点的压力问题，超出中学课程标准的范围

【例5】如图2，质量为M的光滑半圆形凹槽放在光滑的水平地面上，凹槽的半径为R，质量为m的小滑块从凹槽左侧的最高点A由静止释放，当小滑块运动到凹槽的最低点B时，已知重力加速度为g，下列说法正确的是

( )

A.小滑块从A到B的过程中机械能守恒

B.由小滑块和凹槽组成的系统动量不守恒

C.小滑块在最低点对凹槽的压力大小是3mg

【解析】分析方法参考例4，答案为BD。

【评述】关于小球在最低点对凹槽的压力问题，其实介入了非惯性系下牛顿运动定律的应用，只是在最低点时，惯性力恰为0。由于中学课程不涉及非惯性系下惯性力的计算。因此，基于课程标准的要求，尽量规避某位置压力的计算问题。至于强基计划校考备考则另当别论。

3.3 质点相对地面的轨迹论证与周期计算，超出中学课程标准的范围

【例6】质量同为m的小球(可视为质点)从光滑的半圆轨道一端由静止开始下滑，图3轨道与地光滑接触，其质量为M，图4，5中轨道与地固连；图3，4中轨道半径同为r，图5中轨道半径R>r，显然三个小球都会在半圆轨道上做周期性往返运动，周期分别记为T1、T2与T3，试判断这三者之间的大小关系。

图3

图4

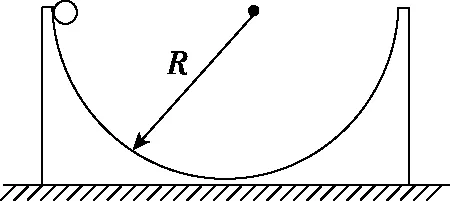
图5

【解析】考查小球转过θ角时各自相对轨道的运动速度大小，以此比较转过相同小角度的时间长短，进而确定周期关系。如图6，设小球相对轨道的速度为v，相对地面的速度为u，轨道相对地面的速度为v′，则

图6

ux=vx-v′=vsinθ-v′，uy=vy=vcosθ

由水平动量守恒定律及系统机械能守恒定律有

m(vx-v′)-Mv′=0

本题中所对应的三段时间分别记为Δt1、Δt2、Δt3。应有如下关系：

图7

3.4 质点在圆弧槽最低点的速度不一定为最大速度

【例7】光滑水平面上有一只内壁光滑的半圆弧槽。半圆弧槽的质量为M，半径为R，如图2，现将一质量为m，可视为质点的小滑块从半圆弧槽的左侧顶端处无初速度释放，已知M=2m，重力加速度为g。求滑块的最大速度。

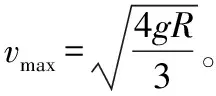
【评述】上述解析有误。在例6分析的基础上，可以得到质点相对地面运动的速度大小为

5sin4θ-36sin2θ+27=0

θ为某位置，m的速度方向与水平方向间的夹角。这表明滑块的最大速度不在槽的最低点。显然，质量关系不同，最大速度的位置不同，因此，在最低点时质点的速度不一定达到最大。