强化模型建构过程 提升模型应用能力
——以2022年全国乙卷第25题为例
新疆 刘杭州 宋书婷
运动与力的相关问题是高中物理的主要研究问题,解决该类问题主要应用动力学知识体系、能量和动量知识体系,常见的运动类模型有匀变速直线运动模型、抛体运动模型、圆周运动模型、碰撞模型等。其中,在建构弹性碰撞模型时,由于碰撞过程的复杂性,多数教师的注意力常放在了碰撞前后的结果讨论上,导致学生对弹性碰撞过程的认识不足,造成了2022年全国乙卷第25题第(2)小问解决方法的错误和困难。运动模型的建构应全面分析运动相关的主要物理量的变化,进而提高学生的认知程度,寻找良好的解决方法。笔者以2022年全国乙卷第25题为例,探讨碰撞模型建构的过程,以期帮助学生深入理解事物发展的全过程,从而实现认知的升华,并举一反三,提升应用物理模型解决问题的能力。
一、真题展示
如图1,一质量为m的物块A与轻质弹簧连接,静止在光滑水平面上;物块B向A运动,t=0时与弹簧接触,到t=2t0时与弹簧分离,第一次碰撞结束,A、B的v-t图像如图2所示。已知从t=0到t=t0时间内,物块A运动的距离为0.36v0t0。A、B分离后,A滑上粗糙斜面,然后滑下,与一直在水平面上运动的B再次碰撞,之后A再次滑上斜面,达到的最高点与前一次相同。斜面倾角为θ(sinθ=0.6),与水平面光滑连接。碰撞过程中弹簧始终处于弹性限度内。求:

图1

图2
(1)第一次碰撞过程中,弹簧弹性势能的最大值;
(2)第一次碰撞过程中,弹簧压缩量的最大值;
(3)物块A与斜面间的动摩擦因数。
二、模型构建
1.完全非弹性碰撞模型
完全非弹性碰撞问题是碰撞问题中的主要问题之一,凡是研究内力作用下(动量守恒)共速问题都应归为完全非弹性碰撞模型。如图3所示,光滑的水平面上,质量为m1的小球A以速度v1和质量为m2的小球B以速度v2发生完全非弹性碰撞。关于完全非弹性碰撞的具体分析见表1。

图3

表1
2022年全国乙卷第25题第(1)小问是考查“动碰静”共速时的动能损失问题,根据完全非弹性碰撞模型的解题方法即可解决。
当两物体达到共速时,弹簧的弹性势能最大,则有
mB(1.2v0)=(mB+m)v0
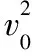
真题第(2)小问是考查“动碰静”共速时的相对位移问题,由于力在整个过程中是变化的,且力的变化并不是线性的,故不能用平均力做功来解决。根据完全非弹性碰撞模型可从动力学和动量两个角度进行分析,但都必须应用微元后累计(微积分)的思想。
角度一:动力学方法
方案一:应用加速度、速度、位移的对应关系分析

若某时刻A的速度为vA,则B的速度为
若t时刻A的位移为xA,则B的位移为
当t=t0时,xA=0.36v0t0,则有xB=1.128v0t0
第一次碰撞过程中,弹簧压缩量的最大值
Δx=xB-xA=0.768v0t0
方案二:结合图像面积分析


图4
xB=1.2v0t0-s2=1.128v0t0
解得Δx=xB-xA=0.768v0t0
角度二:动量方法
根据完全非弹性碰撞模型中两物体间的位移关系可得到mBxB+mxA=(mB+m)v0t0,又xA=0.36v0t0,代入可得xB=1.128v0t0,则Δx=xB-xA=0.768v0t0。
【体会】通过对真题第(2)小问及完全非弹性碰撞模型的应用,可以清晰地感受到完全非弹性碰撞模型中各个物理量与物体的质量密切相关,可以说完全非弹性碰撞模型中加速度、速度、位移、能量损失是以一定的方式、根据质量关系分配的。
2.反冲运动模型
通过上述分析,还可以让学生应用逆向思维,从反冲运动的角度进行思考。实际上完全非弹性碰撞模型的逆过程正是反冲运动模型。反冲运动可认为是共速物体在内力的作用下分裂成两个物体的过程,具体分析见下表2。

表2
真题第(2)小问若应用逆向思维(或研究两物体分离过程)可视为反冲运动模型,可从动力学和动量两个角度进行分析。
角度一:动力学方法
若以v0为参考系,则两物体做反向变加速运动

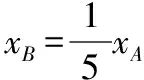
当t=t0时,如图5,v-t图像的面积可知,xA=s1=v0t0-0.36v0t0=0.64v0t0,则有xB=s2=0.128v0t0

图5
第一次碰撞过程中,弹簧压缩量的最大值Δx=xB+xA=0.768v0t0
角度二:动量方法
若以v0为参考系,根据反冲运动模型的位移关系易得
xA=s1=v0t0-0.36v0t0=0.64v0t0

【体会】从逆向思维(或研究两物体分离过程)角度解决该问题的方法相对简单,在选取适合参考系的情况下,不难发现两物体的加速度、速度、位移都与质量成反比,体现了质量在描述物体运动状态中的不可或缺性,突出了动量这一物理量在描述物体运动状态时的全面性、优越性和重要性。
3.弹性碰撞模型
弹性碰撞模型是碰撞问题的难点,弹性碰撞包含了动量守恒问题中的几乎所有情况,弹性碰撞的难点在于对碰撞过程的理解和碰后速度的求解,具体分析如下表3。
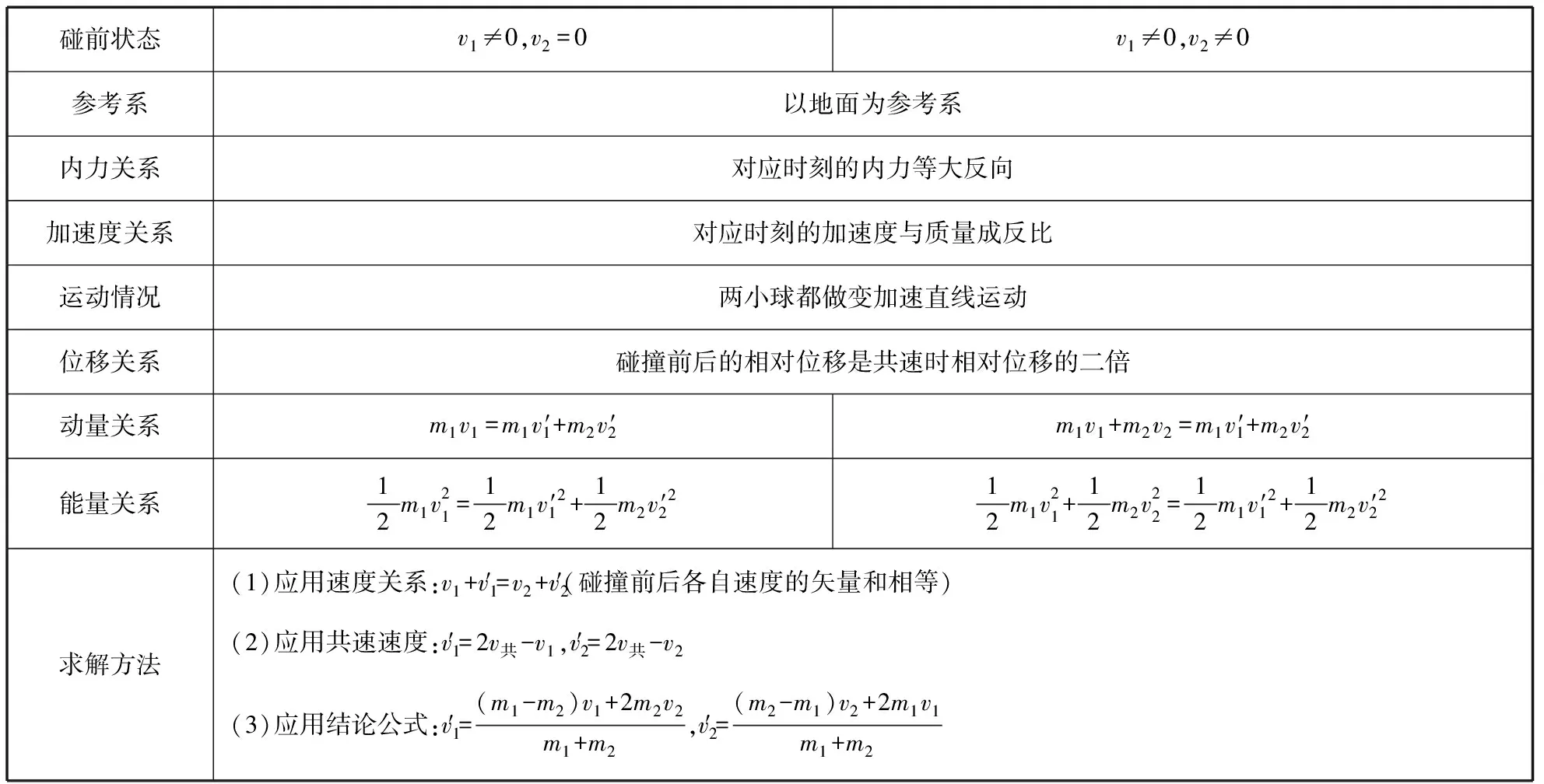
表3
真题第(3)小问的难点在于求解弹性碰撞“动碰动”中的速度,可应用弹性碰撞模型求速度的方法快速得出速度关系,再结合动能定理或动力学方法求出最终结果。
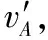

设物块A在斜面上滑行的长度为L,上滑过程有
联立解得μ=0.45
【体会】关于弹性碰撞速度的求解因人而异,相较其他方法,用共速速度求解更便捷,对于动摩擦因数可根据个人习惯应用动力学方法或能量方法、选取适合的过程进行求解,但应用弹性碰撞模型求出物块A第一次滑下斜面的速度是解决问题的关键。
三、结语


