函数及其图像在高中物理中的应用例析

甘肃 高会平 陈永青

函数是描述变量之间依赖关系的工具，其图像则是反映变量关系的一种直观工具。在高中物理的学习中，确定物理量之间所蕴含的函数关系并画出图像，就能更准确、直观、形象地描述物理现象和规律以及确定物体运动变化规律，尤其是对于那些比较复杂或者无法准确地画出图像的运动变化规律，则可利用函数或函数图像做半定量或定性的分析、判断等，这是函数性质及其图像在物理学中最为重要的、也是最为直接的应用。本文就从以下三个方面对函数及其图像在高中物理学中的应用做一归纳性的分析。

一、利用函数及其图像描述物理现象和物理规律

物理规律是指某个物理量与其他物理量之间的一种关系式，其本质就是一种函数关系式，在数学中变量更具有一般意义，但在物理学中，每一个变量都具有特定意义。

物理规律的建立，首先是测定物理量，其次是整理数据，第三是作图，最后是分析图像特点，总结变量之间所蕴含的关系；从数学角度看，则是根据图像求出了函数解析式。具体可以从以下两方面来看待物理规律。

一是由物理量之间的关系式确定函数关系式及其图像，且不同的函数图像具有确定的物理意义，常见的有以下几方面：(1)截距，它反映了所研究对象的一个初始状态；(2)交点，即图像中图线与图线相交的点，反映了两个不同的研究对象在交点处有相同的物理量；(3)极值点，它表示在该点附近物理量的变化趋势的不同；(4)斜率，表示两个物理量增量的比值可作为另外一个物理量的值，如s-t图像的斜率为速度、v-t图像的斜率为加速度、Φ-t图像的斜率为感应电动势、U-I图像的斜率为负载的电阻等。(5)面积，它表示的物理意义在不同章节中有所不同，如图1所示的v-t图像，在t1～t2时刻内，图像与横轴围成的面积表示位移。再如图2所示的p-V图像，其等温线下方的面积表示一定质量的气体的体积从V1到V2过程中所做的功。这也是区别于数学中的函数性质的抽象性这一特点。

图1

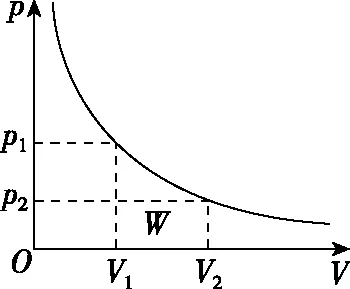
图2

二是对一些物理现象和规律，可用图像进行形象直观地表示。例如两个等量异种点电荷，其电势的大小随距离的变化而变化，如图3所示，沿电场线方向电势降低。以正点电荷为参考点，左右两侧电势都是降低的；以负点电荷为参考点，左右两侧电势都是升高的。可见，在整个电场中，正点电荷所在位置电势最高，负点电荷所在位置电势最低，以两点电荷所在直线为x轴，其连线的中点为坐标原点建立坐标系，其电势的大小可用图像形象地表示出来，如图4所示。

图3

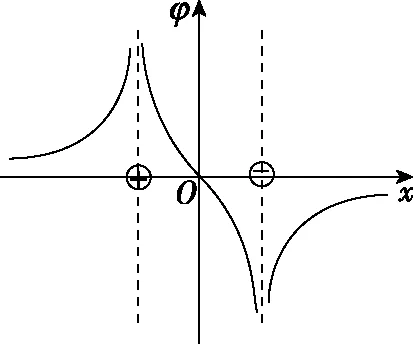
图4

【例1】图5为“探究加速度与力的关系”的实验装置示意图。认为桶和砂所受的重力等于使小车做匀加速直线运动的合力。实验中平衡了摩擦力后，要求桶和砂的总质量m比小车质量M小得多。请分析说明这个要求的理由。

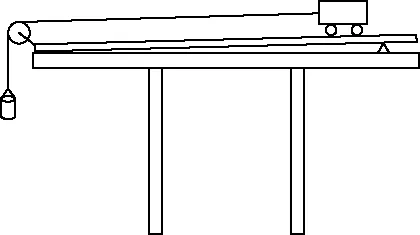
图5

【解析】设斜面与水平桌面的夹角为α，小车与斜面间的动摩擦因数为μ。对于整个系统，根据牛顿第二定律可得

F=mg+Mgsinα-f=(M+m)a①

f=μMgcosα②

因为m≪M，且平衡了摩擦力，小车受到沿斜面向下的重力的分力等于小车受到的摩擦力，所以有Mgsinα=μMgcosα(或α=arctanμ)

在这种满足了桶和砂的总质量m比小车质量M小得多情况下，则可以把对小车的拉力近似地看成桶和砂受到的重力。

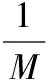
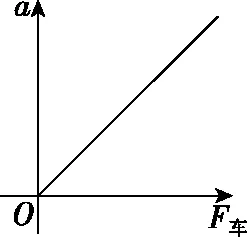
图6

图7

【变式1】将例1中的“实验中平衡了摩擦力后，要求桶和砂的总质量m比小车质量M小得多”改为“实验中要求桶和砂的总质量m比小车质量M小得多，但未平衡摩擦力”，其余条件不变，探究小车加速度和拉力、小车加速度和小车质量之间的关系。

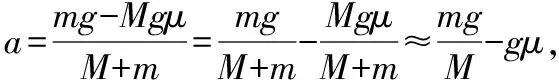
图8

图9

【变式2】将例1中的“实验中平衡了摩擦力后，要求桶和砂的总质量m比小车质量M小得多”改为“实验中要求桶和砂的总质量为m，小车质量为M，且平衡了摩擦力”，探究小车加速度和拉力、小车加速度和小车质量之间的关系。

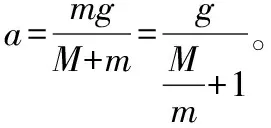
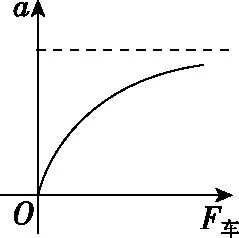
图10

图11

【点评】物理中量与量之间的关系，其本质就是数学中的函数，解决问题的重点在于寻找物理量之间的规律，即他们之间的函数关系。因此，教师在教学中应帮助学生建立用函数思想解决物理问题的意识，一要抓住图像、解析式(公式)以及其性质特点来理解规律，二要抓住变量背后实际的物理意义，同时二者相结合，实现对物理规律的深刻理解和灵活应用。

二、利用函数及其图像确定物理仪器的刻度规律

函数是描述客观世界中变量关系和规律的最为基本的数学语言，尤其在物理学中解决一些物理量随另一个物理量均匀变化的例子很常见，如在讨论物体做匀速直线运动的位移随时间均匀变化；在弹性限度内，弹簧的伸长量随拉力的变化而均匀变化；对一定质量理想气体，其温度随着吸收的热量的改变而均匀变化等，这些都能用一次函数快速而有效地解决；再如漂浮在液面的密度计，排开液体的体积是液体密度的反比例函数；阻值一定的电阻丝，发热功率是两端电压的二次函数等。根据这些问题的函数模型，可以利用函数性质及其图像探究一些物理仪器刻度的变化规律。

【例2】某同学使用轻弹簧、直尺、钢球等制作了一个“竖直加速度测量仪”。如图12所示，弹簧上端固定，在弹簧旁沿弹簧长度方向固定一直尺。不挂钢球时，弹簧下端指针位于直尺20 cm刻度处；下端悬挂钢球，静止时指针位于直尺40 cm刻度处。将直尺不同刻度对应的加速度标在直尺上，就可用此装置直接测量竖直方向的加速度。取竖直向上为正方向，重力加速度大小为g。下列说法正确的是

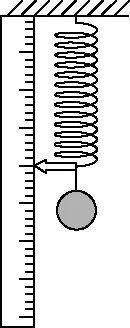
图12

( )

A.30 cm刻度对应的加速度为-0.5g

B.40 cm刻度对应的加速度为g

C.50 cm刻度对应的加速度为2g

D.各刻度对应加速度的值是不均匀的

【解析】根据题意，弹簧不挂钢球时，弹簧下端位于直尺的20 cm处，即可认为弹簧原长为x0=0.2 m，当挂一质量为m的小球时，弹簧长度x1=0.4 m，根据力的平衡得mg=k(x1-x0)，解得k=5mg。当挂重物后弹簧长度为x时，有F弹=5mg(x-x0)，且有F弹-mg=ma，即a=5gx-2g(取竖直向上为正方向)，因此当x=0.3 m时，解得a=-0.5g，故A正确；当x=0.4 m时，解得a=0，故B错误；当x=0.5 m时，解得a=0.5g，故C错误；由于a=5gx-2g是关于弹簧长度x的一次函数，所以各刻度对应加速度的值是均匀的，故D错误。

【点评】对于实验仪器刻度问题，都需要以物理量之间的函数关系式为依据，利用函数性质确定刻度的规律和变化。本题中加速度与弹簧长度之间存在一次函数关系，故刻度变化是均匀的，刻度每变化10 cm，加速度就变化0.5g。本题属于情境性问题，重点考查学生对牛顿第二定律的理解和应用，需要学生具有严密的逻辑推理和探究能力。

三、利用所给图像构建恰当的函数模型

图像不但能直观地表现出物理规律，而且一些图像对应着相关的函数解析式，利用函数解析式能得到精确的解，因此在教学中引导学生关注图像对应的函数模型，并会求函数解析式显得非常重要。高中物理中常见的函数图像有正比例函数、反比例函数、一次函数、二次函数、正(余)弦函数、指数函数、对数函数等。

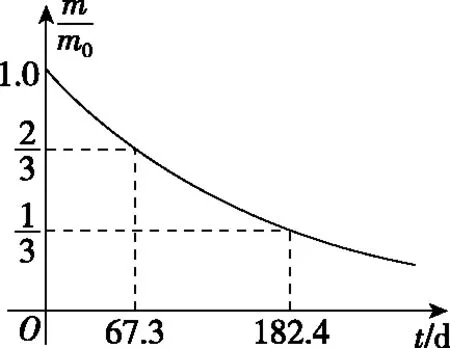
图13

( )

A.67.3 d B.101.0 d C.115.1 d D.124.9 d

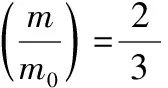
【点评】从所给图像来看，本题是衰变物质量与衰变时间的关系，而且符合指数函数模型，可先求出解析式，进而可准确解出半衰期。对函数图像在物理应用中要注意以下几个方面：(1)横、纵坐标的含义；(2)理解图像反映的是哪些物理量之间的关系以及符合的函数模型，再求出解析式；(3)理解图像中切线斜率、面积、特殊点(原点、拐点、截距、交点)、峰值等的物理意义。

综上所述，物理和数学在高中阶段的学习中是联系最为紧密的两门学科，物理的学习得益于数学严密的推理论证和较强逻辑思维，而且各种数学方法可作为工具，用数学语言表达事物的状态、各种物理量的关系和过程，经过推导、运算、分析、比较、检验、讨论，最终得出结论。此外，由于数学方法具有高度的概括性和抽象性、逻辑的严密性和结论的准确性、应用的普遍性和可操作性的三个特征，所以在高中物理教学与复习备考中，教师应尽量运用数学方法和思想研究物理规律，用简明的数学公式、数学符号系统、形式化的语言表达物理规律以及规律背后的复杂现象，用函数观点研究各种物理量之间确定的关系和规律，培养学生将数学知识延伸使用到物理学习过程中，以提升学生数学、物理知识的综合应用能力。