如何利用类比方式培养高中生的科学思维——以“类比变力做功和变力的冲量”为例

四川 吴春晓 夏泸林

培养学生的科学思维是高中物理教学的重要内容。在教学过程中当学生接触到一个新的物理量时，由于新概念比较抽象，所以无论是理解概念还是进行求解都比较困难。但是如果能够利用类比法，将新概念和旧概念联系起来，不仅能够强化使用不同方法所需的科学思维，还能反过来帮助学生进一步加深对概念的理解。因此，本文选取了功和冲量这两个概念，同时运用微元法、图像法和间接法，对求解变力做功和求解变力冲量的过程进行了类比，以期达到有效培养学生科学思维的目的。

1.从求解变力做功到求解变力的冲量

动量分析和能量分析在物体动力学的分析中举足轻重。目前，在高中物理教学中，对变力做功已有非常全面地探讨，对比之下，对变力冲量的探讨则稍显薄弱。所以，在不同的物理情境中，利用多种方法求解变力的冲量不仅能够培养学生的科学思维，还能起到引导学生进行科学探究的作用。表1对比了在变力做功和变力的冲量两种情境下应用不同方法的具体细节，具体的分析将在后文展开。

表1 求解变力做功和变力冲量的方法对比

2.求解变力的冲量的不同方法

2.1 微元法：同种方法不同应用，深化矢量观念

微元法是处理物理问题非常基本和重要的一种方法，从处理运动学中v-t图像的面积的物理含义开始，在之后很多问题的处理中也都会用到。如果学生在整个高中物理学习历程中，通过螺旋上升的方式，在不同的章节中反复品鉴微元法的精妙之处，对于提升学生的科学思维能力有很大的帮助。在求解变力的冲量的情境中，运用微元法不仅能进一步提升学生的科学思维能力，还能从一个全新的视角来审视矢量合成的观念，从而达到物理观念、科学思维、科学探究协同提升的效果。

【例1】利用微元法求解摩擦力的冲量

如图1所示，质量为m的物体在细绳的牵引下，在动摩擦因数为μ的水平面上，做半径为R的圆周运动。从A点沿逆时针方向运动到B点的过程中，由于其摩擦力方向时刻和运动方向相反，所以在物体运动半个圆周的过程中，利用微元法可以快速地得出滑动摩擦力对物体所做功为W=-μmgπR。

图1

图2

【例2】利用微元法求解圆锥摆支持力的冲量

微元法还可以用来求解圆锥摆中支持力的冲量。

如图3所示，在半顶角为θ的光滑圆锥中，距离O点高度为h的水平面内有一个质量为m的小球做匀速圆周运动。求小球从A运动到B经过半个圆周的过程中，圆锥对小球支持力的冲量大小。

图3

图4

【例3】利用微元法求解安培力和洛伦兹力的冲量

对于在磁场中运动的带电粒子而言，即使其在磁场中不做匀速圆周运动(比如在洛伦兹力和重力的作用下做摆线运动)，也可以通过求解洛伦兹力的冲量来分析问题。同样采取的是微元法的方式I=∑qvyBΔt=qBy=mΔvx。此外，还能得到粒子由于有竖直方向上的速度会产生水平方向上的冲量的美妙结论。

2.2 图像法：同种模型不同视角，深化函数观念

物理问题的分析与解决离不开数学知识，在物理中运用数学知识对学生的科学思维发展很有帮助。函数中的自变量和因变量之间的关系，不仅在数学学科中非常重要，在物理学科中也非常关键。函数的观念中不仅涉及了自变量和因变量的因果关系，还能反映出因变量随着自变量的增加而变化的情况，从而达到预测物理现象和情境的目的。对于弹簧弹力而言，如果取位移为自变量，则图像是一条过原点的直线；对于弹簧振子而言，如果取时间为自变量，则是正余弦函数图像。物理量因不同的自变量而遵循不同的规律，考查了高中物理学科核心素养中的科学推理能力。

【例4】如图5所示，一轻弹簧与质量为m的物体组成弹簧振子，物体在A、B两点间做简谐运动，点O为平衡位置，C为O、B间的一点。已知振子的周期为T，某时刻物体恰好经过C向上运动，则从该时刻起的半个周期内。以下说法正确的是

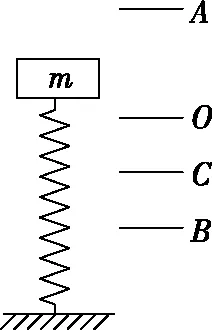
图5

( )

A.物体动能变化一定为零

B.弹簧弹性势能的减少量一定等于物体重力势能的增加量

【答案】AB

【评析】笔者对AB两个选项的分析不再赘述。对于C选项而言，物体所受的弹力和重力的合力才是回复力，而C选项误认为回复力的冲量等于重力的冲量，故C选项错误。

可以看出，当弹力冲量IT方向向下时，并不能直接判断IT和重力冲量IG的大小关系。为了进一步研究可以采用多种方法，这里先利用图像法分析IT。

如图6所示，取竖直向下为正方向，在简谐运动的位移—时间图像的基础上，将纵轴与弹簧的劲度系数k相乘，就能得到回复力—时间图像，于是验证了合外力的冲量必定竖直向下。由于弹簧原长位置必在平衡位置的上方，所以实际上C位置处弹簧的形变量会大于相对于平衡位置的位移。如图7所示，将图像向下平移或者将横轴向上平移到t′位置，此时图像和横轴所围成的面积即为弹簧的冲量。但是，由于弹簧原长位置未知，所以横轴向上平移的长度无法确定。通过图7所示的图像和t′轴所围成的面积可以发现，IT的方向可能向上、可能向下、也可能为零。

图6

图7

综上分析可知，利用图像求解冲量时，不仅能够解决比较常规的一次函数图像问题，还能解决正余弦函数图像问题。通过图像的绘制与分析能够大大减少计算量。

2.3 间接法：同种情境不同路径，深化全程观念

无论是动能定理还是动量定理都更加关注初末的状态量变化，这样全程的思路能够在已知动能或者动量改变的情况下，求出某个力的做功或者冲量。这对于某些难以直接求解的变力做功或者变力的冲量是以一种非常好的方式。

前文中我们利用了微元法直接求解例2情境中的支持力的冲量，但是对于物体运动半个圆周过程中也可列出动量定理

需要说明的是，这个式子中的各个物理量并不共线，所以需要进行矢量合成。如图8所示，通过勾股定理可得

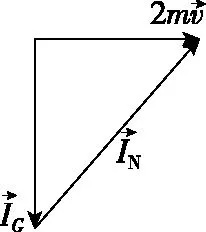
图8

代入之前计算出来的v和t，则得到和前面微元法一样的答案

【点评】在这种情况下，与微元法相比，间接法更为简单直接，但是对于初学者而言，这两种重要方法的掌握都非常重要，所以教师在演示相关方法的时候不能厚此薄彼，而是要将不同的方法都清晰地展现给学生，然后留给学生时间，让他们通过亲自体验的方式，体会不同方法之间的差异，从而才能更立体地提升其科学推理能力。类似地，教师还可以给学生创设如下的情境。

【例5】如图9所示，质量为m的小球用绳悬挂于天花板上的O点，现将小球拉至A点由静止释放，历时t小球运动至B点时的速度为v，求此过程中绳上弹力的冲量。

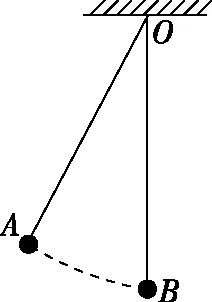
图9

图10

【点评】该处理方式可以进一步让学生认识到动量定理和动能定理在处理问题时的相同和不同之处。其相同之处在于可以回避直接求解运动过程中某个力的做功或者冲量；不同之处在于动能相关物理量都是标量，而动量相关的物理量都是矢量，学生需要意识到两者的不同之处，且必须在实际的应用场景中反复运用和思考。

同样的，在前文提到的例4中，除了使用图像法，还可以用间接法求解弹簧弹力的冲量。具体解法为，假设简谐运动的振幅为A，平衡位置距离原长处的距离为x0，C点距离平衡位置的距离为x，并且取原长所在处为重力的零势能面，则可以通过从B点运动到C点的机械能守恒列式

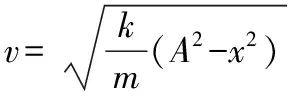
3.总结

为了培养学生的科学思维，本文梳理了微元法、图像法、间接法在求解变力做功和变力的冲量的应用场景。通过对比发现，即使是同为微元法，在求解变力做功时是标量求和，而在求解变力的冲量时是矢量求和，这样的对比能够再次深化学生的矢量观念。即使是同样的弹簧模型，求解变力做功的图像是正比例函数，而求解变力的冲量的图像则是余弦函数，对此能够深化学生对自变量和因变量关系的理解。所以，在教学过程中，教师应该明确求解变力做功和求解变力冲量的微元法之间的区别；进一步理解平均值的物理含义。与此同时，引导学生对比不同方法的特点也很有必要，只有学生亲身体验过不同方法的求解过程，才能真正掌握找寻最优方法的途径。