2022年高考湖南卷物理压轴题探析

湖北 黄尚鹏

本文先介绍如何用递推法求解2022年高考湖南卷物理压轴题的第(3)问，总结了求递推数列通项公式的两种常用方法，即累加相消法和构造等比数列法，以期帮助广大读者深入理解递推法，掌握递推法的应用技巧，既而进一步探究篮球自由弹跳过程运动的总路程问题。

一、对原题的分析与解答

图1

(1)求篮球与地面碰撞的碰后速率与碰前速率之比；

(2)若篮球反弹至最高处h时，运动员对篮球施加一个向下的压力F，使得篮球与地面碰撞一次后恰好反弹至h的高度处，力F随高度y的变化如图2所示，其中h0已知，求F0的大小；

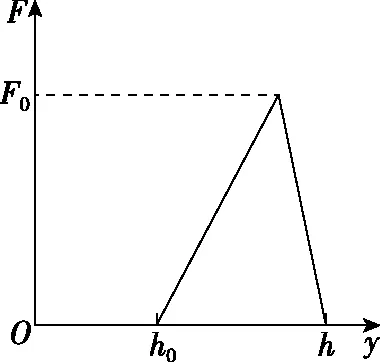
图2

(3)篮球从H高度处由静止下落后，每次反弹至最高点时，运动员拍击一次篮球(拍击时间极短)，瞬间给其一个竖直向下、大小相等的冲量I，经过N次拍击后篮球恰好反弹至H高度处，求冲量I的大小。

【分析与解答】(1)篮球从离地H高度处由静止下落的过程，设篮球与地面碰撞的碰前速率为v1，由动能定理得

篮球与地面发生一次非弹性碰撞后反弹至离地h的最高处的过程，设篮球与地面碰撞的碰后速率为v2，由动能定理得

设篮球每次与地面碰撞的碰后速率与碰前速率之比为

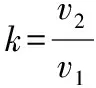
(2)篮球反弹至最高处h时，运动员对篮球施加一个向下的压力F，力F随高度y的变化图像与横轴围成的图形的面积表示变力F所做的功，由动能定理得

联立①④可得

图3

第n次反弹至最高点运动员拍击篮球后，下落过程由动能定理得

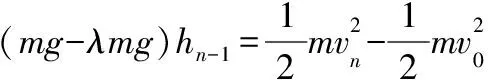
反弹后上升过程由动能定理得

篮球与地面碰撞的碰后速率与碰前速率之比为

数列{hn}由递推公式给出，如何求解它的通项公式呢？可以采用以下的两种方法。

方法一：构造等比数列法

引入待定常数α，使hn-α=p(hn-1-α)，则hn=phn-1+(1-p)α

故数列{hn-α}是以h0-α=h-α为首项，p为公比的等比数列。

因此hn-α=pn(h0-α)=pn(h-α)，即hn=pn(h-α)+α

方法二：累加相消法

递推公式hn=phn-1+q两边同时除以pn，得

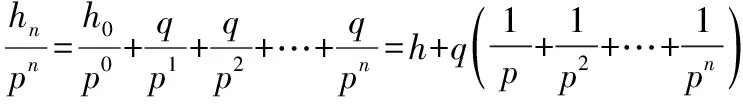
根据等比数列求和公式得

同样得到hn=pn(h-α)+α，代入p和α的表达式后即得数列{hn}的通项公式

因此，冲量

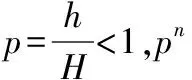
二、试题评析

本题以拍篮球为情境，综合考查动能定理、变力做功、动量定理等主干知识，是一道典型的动量与能量结合的综合题。本题第(1)问考查动能定理的应用(当然也可用运动学公式和牛顿第二定律联立求解)。第(2)问在考查动能定理的基础上进一步考查求解变力做功的一种常用计算方法——面积法，即力F随高度y的变化图像与横轴围成的图形的面积表示变力F所做的功，这两问都很基础，不偏不怪。第(3)问难度较大，考查了一种重要的数学方法——递推法，考查利用数学知识解决物理问题的能力。所谓递推法，即当问题中涉及的物理过程较多，且各物理过程具有相同的特点和遵循相同的规律时，可选取有代表性的任意一物理过程进行分析，得出联系相邻物理过程的相关物理量的递推关系式，再根据递推公式求解相关物理量的通项公式，从而解决问题的一种科学思维方法。累加相消法和构造等比数列法是求递推数列通项公式的常用方法，只要我们抓住递推数列的递推关系，分析结构特征，善于合理变形，就能找到解决问题的有效途径。为使学生深入理解递推法，掌握递推法的应用技巧，再举一例如下。

在如图4所示的电路中，S是一单刀双掷开关，R1、R2为定值电阻，C1和C2为两个平行板电容器，初始时刻，两个电容器都不带电。S掷向a时，C1获电荷量为Q，当S再掷向b时，C2获电荷量为q。问经过n次S掷向a，再掷向b后，C2将获得多少电荷量？

图4

【分析与解答】设S第n次由a掷向b后，电容器C2的电荷量为qn(n≥1)，显然q1=q

每次S接通a后，电容器C1的电荷量都为Q=C1ε

数列{qn}由递推公式给出，如何求解它的通项公式呢？可以采用以下两种方法。

方法一：累加相消法

方法二：构造等比数列法

因此qn-λ=(q1-λ)kn-1

显然用“递推法”解题的关键是导出联系相邻物理过程的相关物理量的递推关系式。

三、变式探究篮球自由弹跳过程运动的总路程

【变式探究(一)】本题第(3)问改为篮球从H高度处由静止下落后，每次反弹至最高点时，运动员并不拍击篮球而是让篮球在空中自由弹跳直致最终静止于地面，求篮球自由弹跳过程运动的总路程。

【变式探究(二)】本题改为质量为m的篮球从离地H高度处由静止下落，与地面发生一次弹性碰撞后反弹至离地h的最高处。设篮球在运动过程中所受空气阻力的大小恒定，且篮球每次与地面的碰撞为弹性碰撞，求篮球在空中自由弹跳过程运动的总路程。

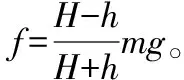
证明：第n次反弹至最高点后，下落过程由动能定理得

反弹后上升过程由动能定理得