重力与万有引力关系的模型建构与试题编制
福建 郑行军
万有引力的试题编制是以万有引力定律为基础,融合圆周运动、重力、开普勒定律等进行综合情境设计,对于学生的知识理解能力和空间想象能力都有较高的要求,其中万有引力和重力的关系问题作为本章重要知识点之一,其理解深度与应用层次对问题的解决有较大影响。本文对两者的关系及试题编制思路进行梳理,希望能对大家有所帮助。
一、重力与万有引力关系的模型分析
1.地表且地球M(或某中心天体)自转影响不能忽略
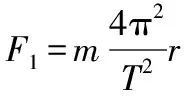

图1
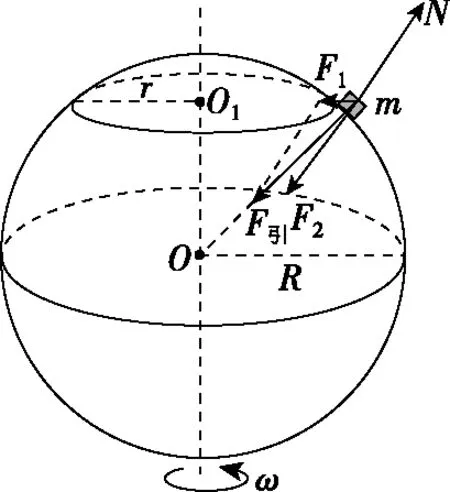
图2
2.地球M(或某中心天体)上方高空
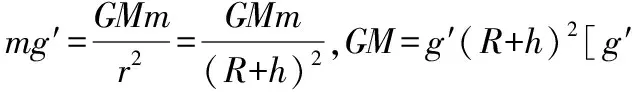
二、试题情境设计与编制
1.不同天体表面的重力加速度比较分析
设计思路:以两个或多个不同天体为信息载体设计试题情境,构建地表重力与万有引力的定量关系,作为核心考点拓展天体表面的重力加速度、天体质量、天体密度和环绕天体问题等,题设条件不涉及中心天体的自转问题。
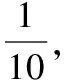
( )

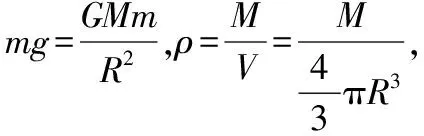
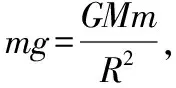
2.同一天体不同高度的重力加速度比较分析
设计思路:聚焦同一中心天体作为参考载体,选择高空不同位置或地表的两个不同研究对象(实物或环绕天体),通过重力与万有引力关系式比较重力加速度关系,分析加速度、中心天体质量、密度、环绕问题等。
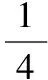
( )
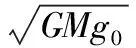
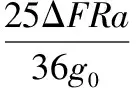
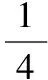

3.同一天体表面不同纬度的重力加速度比较分析
设计思路:在同一天体表面的不同纬度选择两个或多个不同位置做为重力加速度评测参考,不同地表位置的物体在研究受力关系时要考虑中心天体自转的影响,结合重力加速度和向心力的动态关系分析重力加速度、向心力、向心加速度、地表支持力、自转线速度、角速度等物理参量的变化或进行定量计算。
【例3】用弹簧测力计称量一个相对于地球静止的小物体的重量,随称量位置的变化可能会有不同的结果。已知地球质量为M,自转周期为T,引力常量为G。将地球视为半径为R、质量均匀分布的球体,不考虑空气的影响。设在地球北极地面称量时,弹簧测力计的读数是F0。

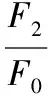
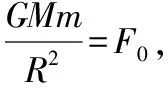
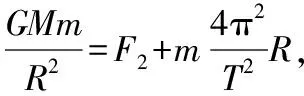


图3
4.天体内外不同位置的重力加速度比较分析
设计思路:以某一天体作为研究对象,在天体内部腔体、表面或高空选择两个或多个位置作为比较,分析不同位置的万有引力或重力加速度关系等。
【例4】人类对自然的探索远至遥远的太空,深至地球内部。若地球半径为R,把地球看作质量分布均匀的球体。某地下探测器A的质量为m,深入地面以下h处,假设h以上的地球球壳物质对探测器A的引力为零;另一太空探测器B质量也为m,围绕地球做圆周运动,轨道距离地面高度为d,则地球对太空探测器B和地下探测器A的引力之比为
( )
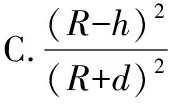
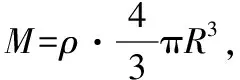
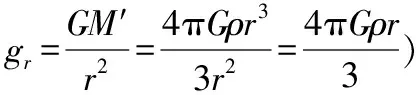

图4
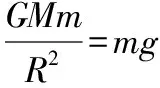
5.地面或高空关联物体的运动问题
设计思路:设计地面或高空的物体运动为试题情境,通过分析物体的运动规律,结合运动学、动力学、功能关系等力学知识,关联出运动与天体表面或高空的加速度关系,延拓中心天体质量、密度、环绕天体的运动、变轨、发射问题等。
【例5】航天员飞到一个被稠密气体包围的某行星上进行科学探索。他站在该行星表面,从静止释放一个质量为m的物体,由于气体阻力,其加速度a随下落位移x变化的关系图像如图5所示。已知该星球半径为R,引力常量为G,忽略行星自转产生的影响。下列说法正确的是

图5
( )


【点评】当运动涉及重力加速度的试题编制中,题目信息一般会呈现近地或高空的物体运动规律,如自由落体、竖直上抛、平抛、圆周运动等,并以此构建运动和重力加速度的关系,具体的试题特征是天体表面或高空的重力加速度一方面与天体有关[GM=gR2或GM=g′(R+h)2];另一方面与物体运动关联,利用重力加速度为纽带建构物体运动和万有引力、天体运动之间的关系(图6),因而可以实现地面和高空的有机统一,达到同时考查近地运动和高空天体作用规律的双重目的,具有一定的综合性。
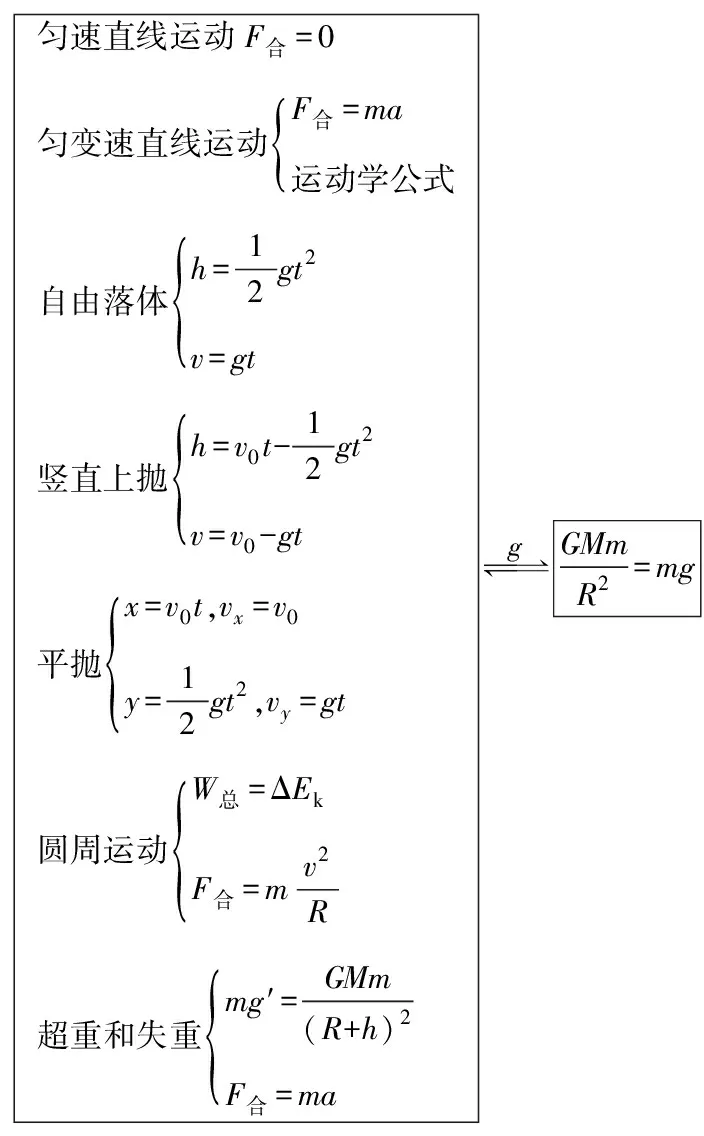
图6
三、小结


