浅谈协变类比思想在高三复习中的应用
重庆 杨天才
1 问题提出
高中物理涉及的思想方法很多,有整体与隔离、分割与积累、类比、降维、等效、极限、对称、图示与图像、守恒、猜想与假设、数学物理方法,其中类比法也叫“比较类推法”“类比推理法”,是一种创造性的平行思维方法,也是研究物理问题常用的方法之一,对解决一些教学难点有至关重要的作用。类比是指根据两类事物的部分特征相似,推出两事物其他方面的特征也可能相似。类比对象间共有的属性越多,则类比结论的可靠性越大,类比能够使主体对已知事物的判断直接过渡到对未知事物的判断,其结论的正确性必须由实验来检验。而协变类比是对象的属性之间可能具有某种确定的函数关系而进行的推理,在高三复习过程中,很多不同板块知识之间的内容有思维的共通性,完全可以用类比思维来解决难点,从而打破板块之间的思维壁垒,使思想方法在这里融会贯通。本文以力学和电磁学中的协变类比为例进行探究。
2 协变类比
2.1 函数关系为(A、B、C为常数)
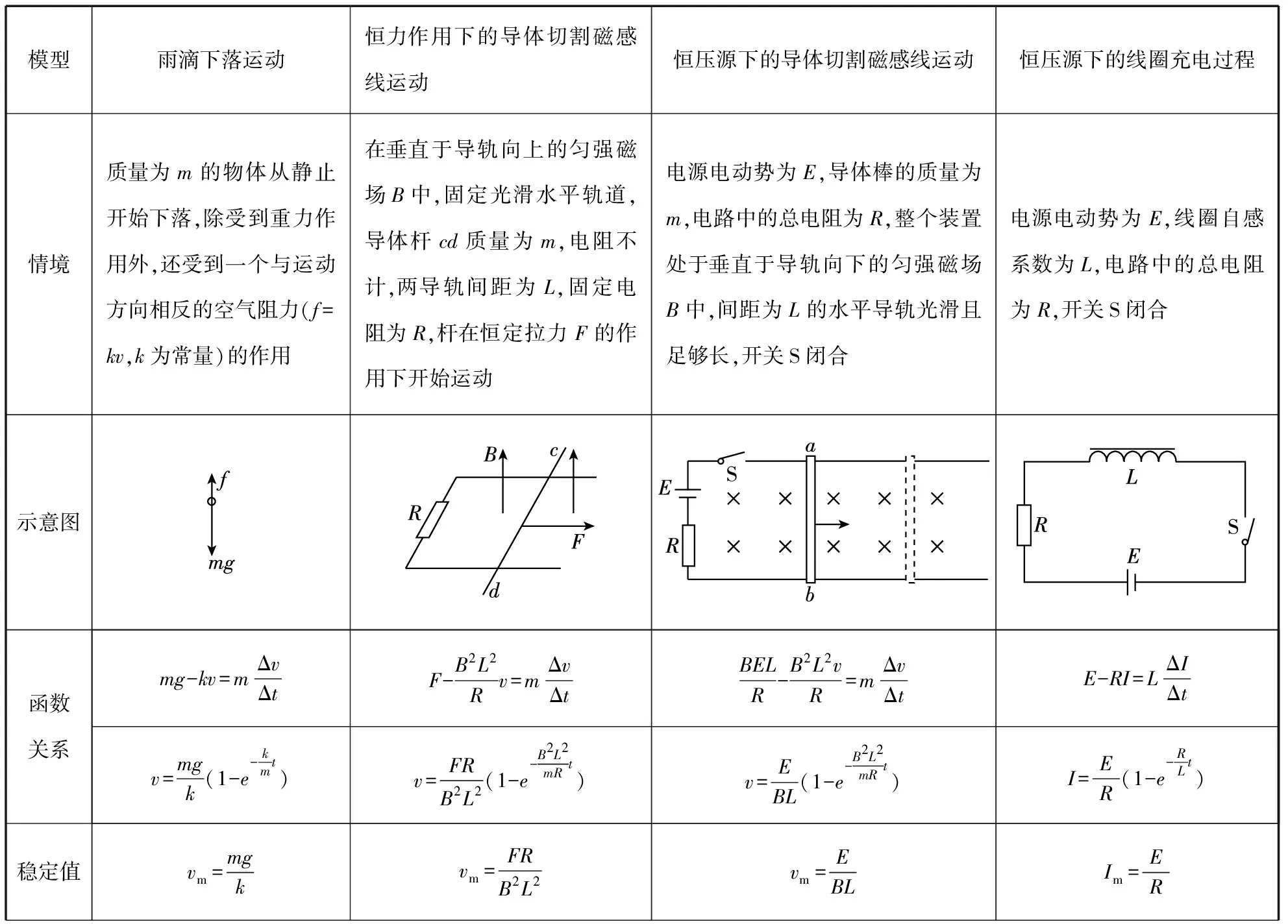
表1
2.2 函数关系为:(A、B为常数)

表2
3 应用举例
【例1】类比是研究问题常用的方法

(2)情境2:如图1所示,电源电动势为E,导体棒的质量为m,定值电阻的阻值为R,忽略电源内阻及导体棒、轨道的电阻,整个装置处于垂直于导轨向下的匀强磁场中,磁感应强度大小为B,间距为L的水平导轨光滑且足够长。闭合开关S,导体棒开始加速运动,闭合开关瞬间开始计时。
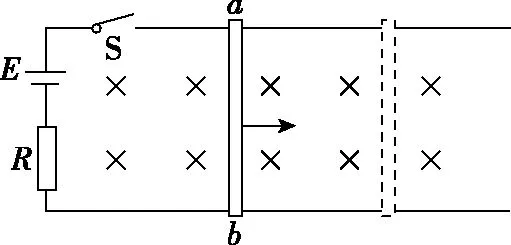
图1
a.求t=0时导体棒的加速度;
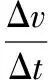
(3)情境3:如图2所示,电源电动势为E,线圈自感系数为L,电路中的总电阻为R。闭合开关S,发现电路中电流I随时间t的变化规律与情境1中物体速率v随时间t的变化规律类似。类比(Ⅰ)式,写出电流I随时间t变化的方程(Ⅲ),并在图3中定性画出I-t图像。

图2

图3

(5)类比情境1、情境2和情境3中的能量转化情况,完成表3。

表3
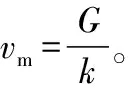
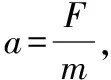
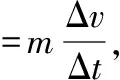
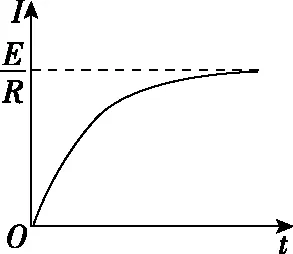
图4

(5)由能量的转化与守恒定律得

表4
【点评】本题考查协变类比思想的具体应用,对于电磁感应中速度随时间、自感现象中电流随时间变化的函数关系,对高中生来说较难,通过与雨滴下落类比,找到它们所满足的方程的共同点,应用协变类比,使问题得以解决。教学中对一些难点的突破,对复杂问题的简单处理,对物理规律的迁移,类比法都是很好的选择。
【例2】类比是研究问题的常用方法
(1)情境1:如图5所示,光滑水平面上的弹簧振子,钢球质量为m、弹簧劲度系数为k,建立如图6中所示的坐标轴。t=0时,将钢球拉至x=A处由静止释放,小钢球只在弹力作用下做往复运动,此过程中弹性势能与钢球动能相互转化。求:

图5
①t=0时刻小钢球的加速度a;

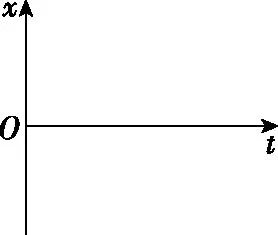
图6
(2)情境2:如图7所示为LC振荡电路,回路中电感线圈的自感系数为L,电容器的电容为C。如图7所示,t=0时闭合开关,此时电容器两极板所带电荷量分别为+Q、-Q。忽略电磁辐射与回路电阻的热损耗,此后LC电路自由振荡。求t=0时刻电容器两极板间的电势差U。

图7
(3)发现情境2中电容器极板的电荷量q随时间t的变化规律与情境1中振子位移x随时间t的变化规律类似。
①类比(Ⅰ)式,写出电荷量q随时间t的变化方程(Ⅱ)和对应的函数表达式。
②从开关S接2瞬间开始计时,在图6所示的坐标系中定性画出电容器上极板的电荷量q随时间t变化的图像,并求出LC振荡电路的振荡频率f。
(4)质量是物体做机械运动时惯性大小的量度,在电磁现象中也存在“惯性”。在情境2中,哪个物理量可用来度量电磁“惯性”的大小。
【解析】(1)弹簧振子的位移x随时间t变化的图像如图8所示。

图8



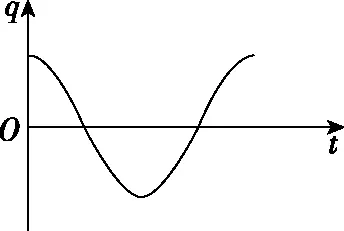
图9
(4)在电磁现象中,物理量自感系数L可用来度量电磁“惯性”的大小。
【点评】电磁振荡中电容器所带电荷量、电容器极板间电压、线圈中的感应电流随时间的函数关系、振荡频率都是高中物理中不涉及推导的,但也是较难掌握的知识,用协变类比,可以大大降低思维难度,简化思维过程,使学生达到“举一反三”“触类旁通”“活学活用”的目的。
4 结语


