滑块与斜面模型的探究

安徽 马仕彪

滑块与斜面模型之间力的关系、运动关系、能量关系和动量关系等都是高考的热点，在历年高考物理试题中屡见不鲜，在平时的练习中也备受瞩目，但滑块与斜面间的细节，如受力分析、运动情况等解决起来却很棘手，特别是当斜面不固定时滑块和斜面间关系的讨论更是困难。本文结合力和运动等知识，深度讨论滑块与斜面之间的关系，以完备高中物理知识体系，增强学生的物理兴趣和解决实际问题的能力。

滑块在斜面上运动时，滑块的运动状态可能是匀速、也可能是加速；斜面可能是固定、也可能是不固定的，笔者下面主要采用整体法与隔离法来研究这几种情况。

一、斜面固定，滑块沿斜面向下做匀速运动的情况

如图1所示，一质量为m的滑块恰好沿倾角为θ的固定斜面M向下做匀速运动。

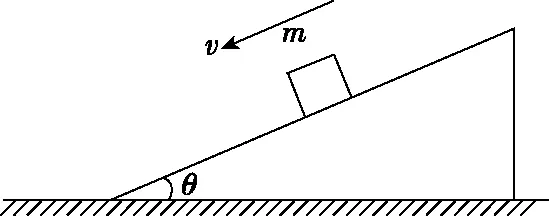
图1

(1)若采用隔离法分别对m和M进行研究

如图2所示，对m进行受力分析，则

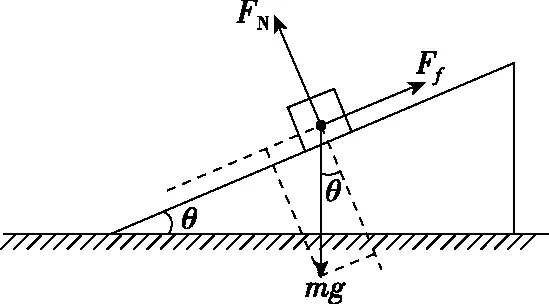
图2

FN=mgcosθ，Ff=μFN=μmgcosθ

由平衡条件知mgsinθ=μmgcosθ，得到μ=tanθ

此亦即滑块能沿斜面匀速下滑的必要条件。

如图3所示，对M进行受力分析

图3

滑块对斜面的摩擦力和弹力沿水平方向的分量分别为

Ffx=Ffcosθ=FNsinθ，FNx=FNsinθ

即Ffx=FNx

(2)若采用整体法进行研究

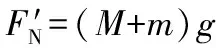
图4

通过比较发现，在判断地面对斜面的弹力和摩擦力时，显然整体法比隔离法更简便。

(3)此时若对滑块施加一个向左下方且与竖直方向夹角为β的恒力F，如图5所示。

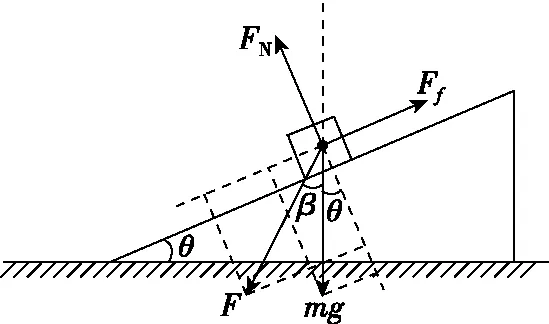
图5

仍先采用隔离法进行研究，对m进行受力分析则

FN=mgcosθ+Fcos(θ+β)

Ff=μFN=μmgcosθ+μFcos(θ+β)

F合=[mgsinθ+Fsin(θ+β)]-[μmgcosθ+μFcos(θ+β)]=ma

现讨论以下几种特殊的情况：

①当F竖直向下，即β=0时，则a=0，滑块继续向下匀速运动，此时相当于在滑块上面再加一个物块；

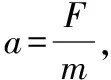
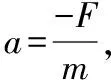
图6

因此，我们得到这样一个结论：当斜面固定不动时，如果物块能沿斜面匀速向下运动，无论在物块上施加什么方向的作用力，在物块沿斜面向下运动的过程中，斜面与地面间一定没有摩擦力。

【例1】如图7所示，m沿固定斜劈匀速下滑，在m下滑的过程中再加一如图中不同方向的作用力，则下列说法正确的是

图7

( )

A.若所加力为竖直向下的F1，m将做匀加速运动，地面对M弹力大于(M+m)g

B.若所加力为沿斜面向下的F2，m将做匀加速运动，地面对M的静摩擦力方向向右

C.若所加力为沿水平向右的F3，m将做匀减速运动，地面对M的静摩擦力方向向左

D.无论在m上加什么方向的力，在m沿斜面向下运动的过程中，M与地面均无静摩擦力的作用

【答案】D

【点评】对于物块的运动情况切忌凭感觉去判断，而是要进行严格的受力分析，通过物块的受力情况来判断其运动情况，在熟练的情况下，可以适当地利用已经储备的物理结论，这样就能既严谨地分析问题，又能快速地解决实际问题。

二、斜面固定，滑块沿斜面做匀加速运动的情况

如图8所示，一质量为m的滑块沿倾角为θ的固定斜面M以加速度a向下做匀加速运动。

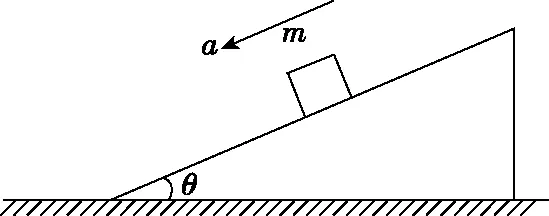
图8

(1)①若采用隔离法分别对m和M进行研究

对m进行受力分析，则

FN=mgcosθ，Ff=μFN=μmgcosθ

由牛顿第二定律得F合=mgsinθ-μmgcosθ=ma>0

则a=gsinθ-μgcosθ，其中tanθ>μ，此亦即滑块能沿斜面匀加速下滑的条件。

对M进行受力分析，则

=Mg+mgcos2θ+μmgcosθsinθ

=(M+m)g-masinθ

滑块对斜面的摩擦力和弹力沿水平方向的分量分别为

Ffx=Ffcosθ=μFNcosθ=μmgcos2θ

FNx=FNsinθ=mgcosθsinθ

②若采用整体法进行研究

将滑块的加速度沿竖直和水平方向进行分解，则ay=asinθ，ax=acosθ

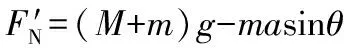
(2)如图9所示，若对滑块施加一个向左下方且与竖直方向夹角为β的恒力F

图9

对m进行受力分析，则FN=mgcosθ+Fcos(θ+β)，Ff=μFN=μ[mgcosθ+Fcos(θ+β)]

由牛顿第二定律得F合=mgsinθ+Fsin(θ+β)-μ[mgcosθ+Fcos(θ+β)]=ma′

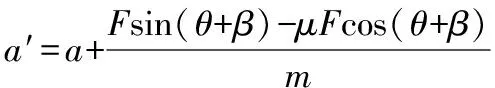
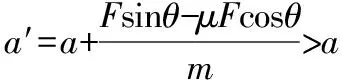
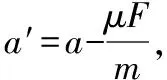
对整体，选择水平向左为正方向，则

解得地面对斜面的摩擦力

【例2】如图10所示，倾角为θ的斜面体放在粗糙的水平地面上，质量为m的物块受到一个与水平方向成α角、大小为F的力的作用下沿斜面向下做加速度大小为a的匀变速运动，已知斜面足够长，且始终静止，则下列说法正确的是

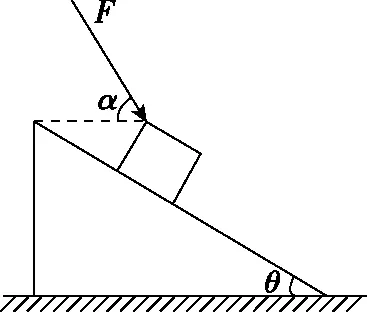
图10

( )

A.若物块向下匀加速运动，地面对斜面的弹力大小为FN=(M+m)g+Fsinα-masinθ

B.若物块向下匀加速运动，地面对斜面的摩擦力大小为Ff=Fcosα-macosθ，方向水平向左

C.若物块向下匀减速运动，地面对斜面的弹力大小为FN=(M+m)g+Fsinα+masinθ

D.若物块向下匀减速运动，地面对斜面的摩擦力大小为Ff=Fcosα+macosθ，方向水平向左

【答案】ACD

【解析】若物块向下匀加速运动，加速度方向沿斜面向下，系统沿竖直方向的加速度为ay=asinθ，在竖直方向上对系统应用牛顿第二定律得(M+m)g+Fsinα-FN=masinθ，则地面对斜面的弹力大小FN=(M+m)g+Fsinα-masinθ，因此A选项正确；系统沿水平向右的加速度为ax=acosθ，在水平方向上对系统应用牛顿第二定律得Fcosα±Ff=macosθ，当Fcosαmacosθ时，等式满足Fcosα-Ff=macosθ，解得摩擦力大小为Ff=Fcosα-macosθ，方向水平向左，因此B选项错误；若物块向下做匀减速运动，加速度方向沿斜面向上，系统沿竖直向上的加速度分量为ay=asinθ，在竖直方向上对系统应用牛顿第二定律得FN-(M+m)g-Fsinα=masinθ，则地面对斜面的弹力大小FN=(M+m)g+Fsinα+masinθ，故C选项正确；在水平方向上对系统应用牛顿第二定律得Ff-Fcosα=macosθ，解得Ff=Fcosα+macosθ，方向水平向左，故D选项正确。

【点评】通过本题的解题过程可以明显看出整体法更简单，过程更干净利落，主要原因是整体法回避了物块与斜面之间的内力，只需要讨论系统的外力即可。当然本题也可以使用隔离法进行研究，但隔离法过程较复杂，运算量较大，但隔离法仍有它自身的优点，即隔离法能让我们弄清楚问题的细节与联系，对问题的认识更加深刻。

三、斜面不固定，滑块沿斜面向下运动的情况

如图11所示，高为h、质量为M、倾角为θ的斜面放在水平地面上，质量为m的滑块轻置于斜面顶端，不计一切阻力，讨论下列问题：

图11

(1)滑块滑离斜面时，滑块和斜面各自的水平位移

(2)运动过程中，滑块和斜面各自的加速度

对滑块在水平和竖直方向上分别应用牛顿第二定律

FNsinθ=ma1x，mg-FNcosθ=ma1y

对斜面应用牛顿第二定律FNsinθ=Ma2

由相对运动特点可知，滑块和斜面两者之间加速度的关系满足a1ycosθ-a1xsinθ=a2sinθ

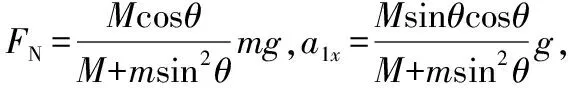
(3)滑块滑离斜面时，滑块和斜面各自速度的大小和运动时间

滑块和斜面的速度关系满足沿垂直于斜面方向的分量相等，即v1ycosθ-v1xsinθ=v2sinθ

滑块从顶端运动到底端的时间

(4)滑块与斜面之间弹力做的功

如图12所示，弹力对滑块做负功，对斜面做正功，其做功代数和为零。弹力对斜面做的功可以运用两种方法进行求解。

图12

方法一：由功的定义WFN=FN·x2sinθ，将以上计算出的FN和x2代入，得

方法二：对斜面应用动能定理

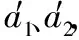
图13

( )

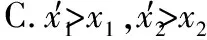
【答案】AD

【解析】设A、B的质量分别为m、M，在物块A上再放一个物块C组成D，相当于A的质量m变大了。

由以上分析，A的加速度大小为

随着m的增加，无法根据表达式直接判断出加速度的变化，现在将表达式进行变形

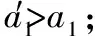
分离时A的速度大小为

分离时B的速度为

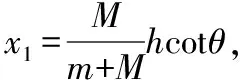
下滑的时间为

【点评】本题要求我们不仅要具备精湛的物理知识，还要具有利用数学知识处理物理问题的能力，因为数学是解决物理问题的工具，对于此类问题要尽可能从定量的角度将问题研究清楚，这样不仅可以增强学生的物理兴趣，更能进一步深度认识物理的本质。此外，本题也可以采用极限法定性进行讨论，各位读者可以尝试研究，这里不再赘述。

四、结束语