明辨“真伪”轴，寻找共同点——以圆周运动比较类选择题为例

江苏 万吉莉 黄 皓

“同轴转动”是圆周运动比较类问题的常见易错点之一，多见于选择题。为帮助学生深度理解“同轴转动”，教师应引导学生通过亲历知识建构和问题解决的过程，明晰“同轴转动角速度相同”的产生原因与适用条件，从而转变迷思概念；在此基础上，通过有意识地反思与审视问题，并进行归纳总结，进而得到高效的解题策略。本文呈现了以上具体的教学实践，旨在为核心考点的复习提供参考。

1 问题背景

依据《普通高中物理课程标准(2017年版2020年修订)》，普通高中学业水平选择性考试需要学生达到学业质量水平4，即能理解所学的物理概念和规律及其相互关系，综合应用所学的物理知识解决实际问题、能将实际问题中的对象和过程转换成所学的物理模型、能对综合性物理问题进行分析和推理，获得结论并作出解释。因此，一轮复习时需要注重知识间的横向编织与纵向串联，进而将所学内容结构化，从而转变迷思概念。

国外学者Tyson等人认为概念转变过程包括四个步骤，详见图1。下文笔者将结合圆周运动比较类选择题对此加以说明。

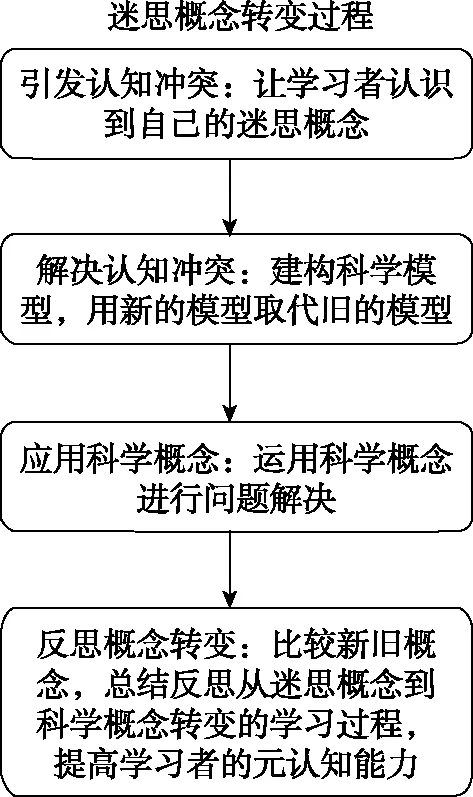
图1

2 教学案例

【例1】如图2所示，一内壁光滑的圆锥面，顶点O在下方，顶角为2α，OO′是竖直轴线，若有A、B两小球，质量mA>mB(可视为质点)，在圆锥的内壁上沿不同的圆轨道做匀速圆周运动，以O点为势能零点，则

图2

( )

A.它们的线速度大小相同

B.它们的周期相同

C.它们的动能相同

D.它们的动能与重力势能之比相同

2.1 引发认知冲突

2.1.1 创设情境

如图3所示，圆盘正在做匀速圆周运动，物体A和B相对圆盘静止，则两者随圆盘一起做圆周运动。

图3

2.1.2 分析概括

教师应用问题链引导学生自主分析概括，具体问题如下：

1.对照俯视图(如图4所示)，假设A物体经时间t运动至A′位置，你能准确画出此时B物体的位置吗？你的依据是什么。

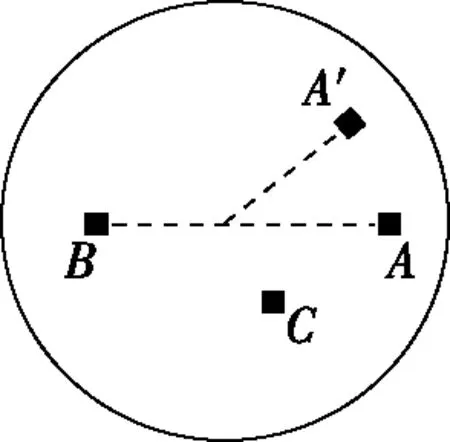
图4

2.如果圆盘上还有一个随之一起转动的C物体，经时间t它又处在什么位置？

3.物体A、B、C及圆盘有什么样的位置关系？他们是否属于同轴转动？角速度是否相同？

4.你还能举出类似的例子吗？

2.2 解决认知冲突

问题1：物体A、B与圆盘相对静止，依据对顶角相等，学生确认物体A、B随圆盘一起转动时在相等时间内转过相同角度，即角速度相同。

问题2：物体C与圆盘相对静止，与A、B不共线；通过实物演示，学生确认物体C与A、B在相等时间内转过相同角度，即角速度相同。

问题3：学生归纳“同轴转动”是指在同一转轴带动下的圆周运动，同时这些物体与转轴表面相对静止，此时“同轴转动角速度相同”成立。

问题4：学生举例，如地球自转、洗衣机的脱水桶(如图5所示)等。学生发现，比如洗衣机的脱水桶，尽管转轴不能直接看到，但显然是在电机驱动下的同轴转动，其等效转轴在圆桶中央。

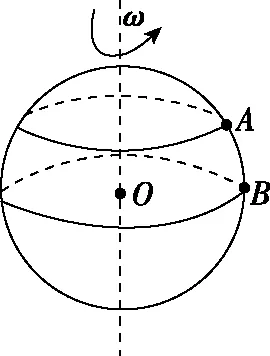
图5

在这个阶段，逐步提出问题链引导学生亲历问题的解决过程；最终明确，在同一转轴带动下，与旋转物体相对静止的物体角速度相同。

2.3 应用科学概念

教师给出巩固练习，要求学生自主分析，快速求解。

【例2】如图6所示，O为半球形容器的球心，半球形容器绕通过O的竖直轴以角速度ω匀速转动，放在容器内的两个质量相等的小物块a和b相对容器静止，b与容器壁间恰好没有摩擦力。已知a和O、b和O的连线与竖直方向的夹角分别为60°和30°，则下列说法正确的是

图6

( )

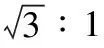
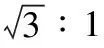
C.小物块a与容器壁之间无摩擦力

D.容器壁对小物块a的摩擦力方向沿器壁切线向下

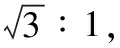
2.4 反思概念转变

反思概念转变阶段是在新的心理模型建立后，在新的问题中迁移应用新模型，使新的心理模型真正成为学习者认知结构的一部分，即科学概念的完整建立。

【例3】如图7所示，2021年10月16日，神舟十三号载人飞船从天和核心舱下方采用“径向对接”的方式实现自主对接。所谓“径向对接”即两对接口在地球半径的延长线上，对接前两者要在相距200米的“保持点”相对静止一段时间，准备好后，再逐步接近到对接点，则

图7

( )

A.飞船在与核心舱相对静止的“保持点”可以不消耗燃料

B.飞船在“保持点”受到万有引力为其圆周运动的向心力

C.飞船在“保持点”运动的线速度大于核心舱运动的线速度

D.飞船在“保持点”的向心加速度小于核心舱的向心加速度

一般情况下，不同轨道处的人造地球卫星都是由万有引力提供向心力；据此可得出“轨道高度越高，线速度、角速度、向心加速度越小，周期越大”的二级结论。同例1一样，学生如直接套用便会错选C选项。正所谓“吃一堑长一智”，学生在经历过对例1的研讨后，开始有意识地审视与反思问题。

2.4.1 审视反思

学生在教师的引导下做如下探究活动：作出飞船和核心舱运动的轨迹圆，标出圆心；核心舱经时间t后运动到某位置，根据题干关键词确定飞船此时位置；寻找核心舱和飞船运动过程中的共同点。

在活动中，学生把实际情境转化成物理情境，通过研讨卫星转动过程，得出飞船和核心舱其实是更广义的“同轴转动”，具有运动学共同点。这里的“轴”不再是具象的某个转轴，而是依据题干关键词“相对静止”等效出来的轴。因此飞船与核心舱角速度相同，应用v=ωr及a=ω2r可得到低轨道的飞船线速度和加速度更小，故D选项正确。此外，两者在“保持点”相对静止时不可能只受万有引力，由于动力装置处于工作状态，当然要消耗燃料。

2.4.2 拓展讨论

【例4】如图8所示，“鹊桥”中继星处于地月拉格朗日点L2上时，会和月球、地球两个大天体保持相对静止的状态。设地球的质量为M，“鹊桥”中继星的质量为m，地月间距为L，拉格朗日L2点与月球间距为d，地球、月球和“鹊桥”中继星均可视为质点，忽略太阳对“鹊桥”中继星的引力，忽略“鹊桥”中继星对月球的影响。则“鹊桥”中继星处于L2点上时，下列选项正确的是

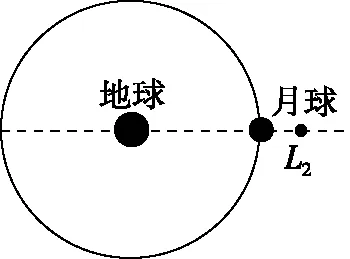
图8

( )

A.地球对月球的引力与“鹊桥”中继星对月球的引力相等

C.“鹊桥”中继星与月球的向心加速度之比L2∶(L+d)2

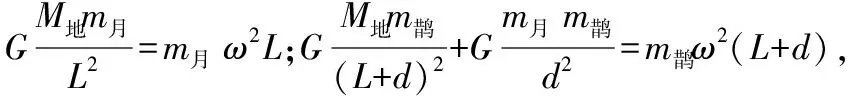
3 解答策略

在亲历模型建构和问题解决过程后，学生发现比较物体间的共同点有利于高效解答圆周运动比较类选择题。学生总结了两类共同点所对应的模型特点和解决方法，如表所示。

运动学共同点动力学共同点模型特点“同带传送”存在或等效存在共同转轴即“同轴转动”两物体向心力来源一致或有类似的受力情况解决方法依据各运动学参量之间的关系进行比较依据牛顿第二定律列方程求解后进行比较

4 结语