例析物理试题改编的常用方法
山东 成树明
试题改编与试卷命制是教学检测、诊断、调控和评价的基础性工作,是教师日常教学工作的一个重要环节。优秀试题是进行有效训练、双减增效的重要保障。对试题进行改编会促进教师的专业成长,同时试题的改编与原创能力也是教师专业素养的体现。笔者下面例谈几种常用的试题改编方法,以期抛砖引玉。
一、积木式重组法
所谓积木式重组法改编试题,就是取几道题中各一部分,然后如搭积木一样经排列组合重新组成一道新题。积木式重组法并非简单地、机械地将试题拼凑组合,而是根据考查要求,遵循学科规律和学科逻辑对原题进行优化重组。
【原题1】利用光电门、遮光片组合可以探究“弹簧的弹性势能与形变量之间的关系”实验装置如图1所示,木板的右端固定一个轻质弹簧,弹簧的左端放置一个小物块(与弹簧不拴接)物块的上方有一宽度为d的遮光片(d很小),O点是弹簧原长时物块所处的位置,其正上方有一光电门,光电门上连接有计时器(图中未画出)。
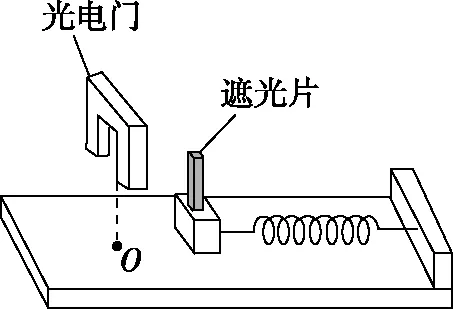
图1
(1)实验开始时,________(填“需要”或“不需要”)平衡摩擦力;
(2)所有实验条件具备后将小物块向右压缩弹簧x1后从静止释放,小物块在弹簧的作用下被弹出,记下遮光片通过光电门的时间t1,物块通过光电门的速度为________;
(3)分别再将小物块向右压缩弹簧x2、x3、…后从静止释放,小物块在弹簧的作用下被弹出,依次记下遮光片通过光电门的时间t2、t3、…;

【原题2】某同学用图2所示实验装置来研究弹簧弹性势能与弹簧压缩量的关系,弹簧一端固定,另一端与一带有窄片的物块接触,让物块被不同压缩状态的弹簧弹射出去,沿光滑水平板滑行,途中安装一光电门,设重力加速度为g。
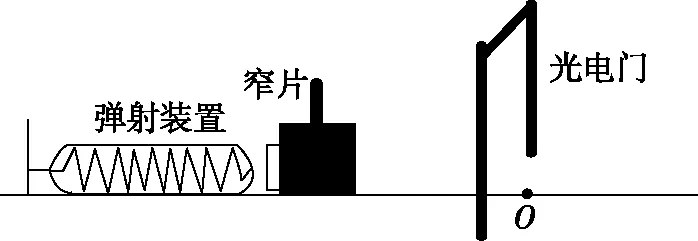
图2
(1)如图3所示,用游标卡尺测得窄片的宽度L为________;

图3
(2)记下窄片通过光电门的时间Δt=10 ms,则窄片通过光电门的速度为________m/s;(计算结果保留三位有效数字)
(3)若物块质量为m,弹簧此次弹射物块过程中释放的弹性势能为Ep=________(用m、L、Δt表示)。
【原题3】为探究弹簧的弹性势能与形变量的关系和测量滑块与水平桌面间的动摩擦因数,某实验小组设计了如图4所示的装置,弹簧的左端固定在水平桌面上,弹簧右端原长位置处固定一光电门,滑块上固定一个遮光条。已知滑块连同遮光条的总质量为m,当地的重力加速度为g。
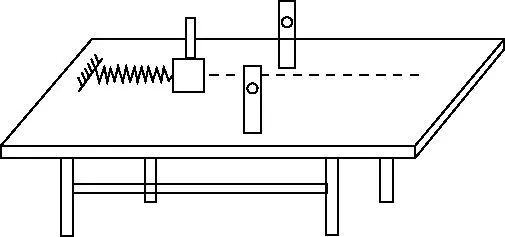
图4
(1)先用螺旋测微器测出遮光条的宽度d如图5所示,则d=________mm。

图5
(2)用滑块(与弹簧不拴接)向左压缩弹簧,并用刻度尺测量其压缩量x,松手后遮光条通过光电门的时间为t,测得滑块停下的位置到光电门的距离为s,则滑块与水平桌面间的动摩擦因数μ=________(用题中的字母表示)。
(3)压缩弹簧时弹簧的弹性势能与形变量间的关系为Ep=________(用题中的字母表示)。
【改编】如图6所示,利用光电门、遮光片组合可以探究弹簧的弹性势能与形变量的关系,弹簧的右端固定在木板上,弹簧的左端放置一小滑块(与弹簧不拴接),滑块的上方有一宽度为d的遮光片,弹簧左端原长位置O处固定一光电门,光电门上连接有计时器(图中未画出),已知滑块连同遮光片的总质量为m,当地的重力加速度为g。
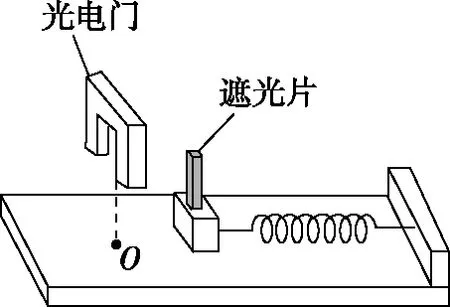
图6
(1)先用游标卡尺测出遮光片的宽度d,如图7所示,则d=________cm;

图7
(2)将小滑块向右压缩弹簧x后从静止释放,小物块在弹簧的作用下被弹出,记下遮光片通过光电门的时间t,则小滑块通过光电门的速度达式为v=________;
(3)又测得小滑块停下的位置到光电门的距离为s,则压缩弹簧时弹簧的弹性势能与形变量间的关系式为Ep=________。
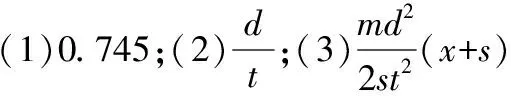
【解析】(1)游标尺是20分度的,则游标卡尺的精确度为0.05 mm,由图7所示游标卡尺可知,其读数为7 mm+0.05×9 mm=7.45 mm=0.745 cm。
【点评】三个原题中的实验装置图中原题1最清晰美观,所以改编试题的实验装置图选自原题1;对于遮光片宽度的测量,游标卡尺就能达到实验要求的测量精度,所以遮光片宽度测量思路选自原题2,并对图3进行了更换。改编试题的设问(1)选自原题2第(1)问,设问(2)选自原题1第(2)问,设问(3)选自原题3第(3)问。改编后试题的三个设问,分别考查游标卡尺读数、瞬时速度测量的两个基本问题及利用动能定理和功能关系测弹性势能与形变量间的关系。
二、题型转换法
题型转换法改编试题,就是将选择题、填空题和计算题等题型中的一种改编成另一种,通常试题的情境不变,而对设问的角度进行改变。
【原题】如图8所示,在倾角为30°的光滑斜面上放置一质量为m的物块B,B的下端连接一轻质弹簧,弹簧下端与挡板相连接,B平衡时,弹簧的压缩量为x0,O点为弹簧的原长位置。在斜面顶端另有一质量也为m的物块A,距物块B为3x0,现让A从静止开始沿斜面下滑,A与B相碰后立即一起沿斜面向下运动,但不粘连,它们到达最低点后又一起向上运动,并恰好回到O点(A、B均视为质点)。试求:

图8
(1)A、B相碰后瞬间的共同速度的大小;
(2)A、B相碰前弹簧具有的弹性势能;
(3)若在斜面顶端再连接一光滑的半径R=x0的半圆轨道PQ,圆弧轨道与斜面相切于最高点P,现让物块A以初速度v从P点沿斜面下滑,与B碰后返回到P点还具有向上的速度,则v为多大时物块A恰能通过圆弧轨道的最高点?
【改编】如图9所示,轻弹簧下端固定在倾角为θ的斜面底端,O点为弹簧的原长位置。一质量为m的物块从A点由静止开始沿斜面下滑,下滑到最低点B后又恰好能回到O点。已知B点到O、A两点间的距离分别为x0、3x0,重力加速度为g,弹簧始终在弹性限度内,不计空气阻力,下列说法中正确的是
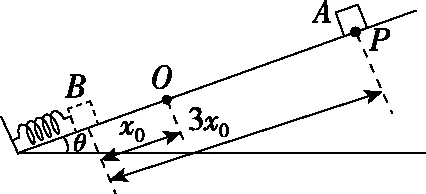
图9
( )


D.从O点到B点滑块动能减少量小于弹簧的弹性势能增加量
【答案】C
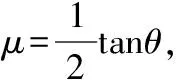
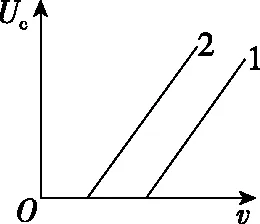
D
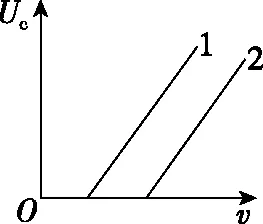
C
D

C
【点评】该题命题初步设想是命制一道含弹簧的能量综合问题。在浏览试题过程中,发现原题情境比较新颖,具备再次创作的条件,于是将原题改编成选择题,情境选取了原计算题的一部分,图9看起来与原题的部分相同,但有本质区别,即原题的A、B是两个物体,改编题的A、B则是同一物体的两个位置,四个选项也是根据的新情境从不同角度进行设置的,达到了预先设想的知识和能力的考查要求。

B
B
三、图像转换法
图像转换法改编试题可以是图像形状不变,改变坐标轴所表示的物理量;也可以是同一物理过程,将一种图像转换成另一种图像等。
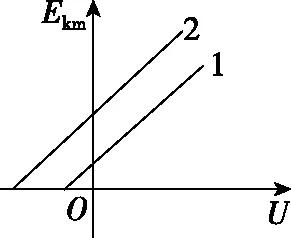
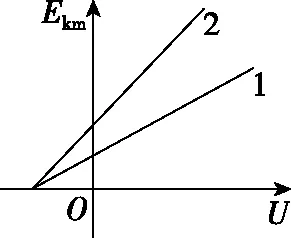
【原题】如图10所示,分别用1,2两种材料作K极进行光电效应探究,其遏止频率ν1<ν2,保持入射光不变,则光电子到达A极时动能的最大值Ekm随电压U变化关系的图像是
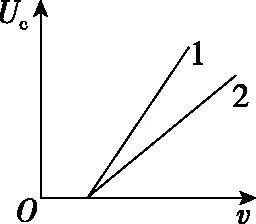
A

A

图10
( )
【改编】如图11所示,分别用1,2两种材料作K极进行光电效应探究,其截止频率ν1<ν2,遏止电压Uc随入射光频率v变化关系的图像正确的是

图11
( )
【答案】D

【点评】原题从图像角度考查光电效应,角度新颖,为了进行变式训练,笔者创作了本题,改编题也是利用图像考查光电效应,原题考查动能最大值Ekm随电压U变化关系,改编题考查遏止电压Uc随入射光频率ν变化关系,由于改编题考查是遏止电压,所以改编题将原题实验装置图中的电源由正向连接改为反向连接。
四、定性与定量转换法
定性与定量转换法改编试题就是将一个定性问题改编成一个定量问题,也可以是将一个定量问题改编成一个定性问题。
【原题】如图12所示,甲、乙两颗卫星以相同的轨道半径分别绕质量为M和2M的行星做匀速圆周运动,下列说法正确的是
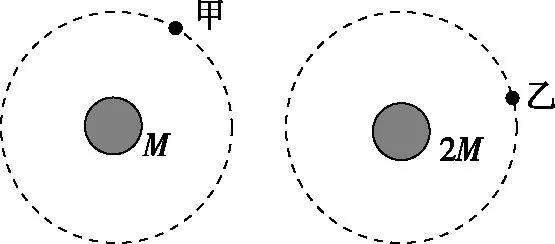
图12
( )
A.甲的向心加速度比乙的小
B.甲的运行周期比乙的小
C.甲的角速度比乙的大
D.甲的线速度比乙的大
【改编1】如图13所示,甲、乙两颗卫星分别绕质量为M1和M2的行星做匀速圆周运动,甲、乙两卫星的轨道半径r1=2r2,运动周期T2=2T1,则两行星的质量之比M1∶M2为

图13
( )
A.32∶1 B.2∶1 C.1∶2 D.1∶16
【答案】A
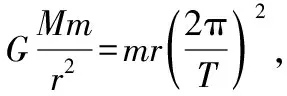
【改编2】如图14所示,甲、乙两颗卫星分别绕半径相等的A、B两行星做匀速圆周运动,甲、乙两卫星的轨道半径r1=2r2,运动周期T2=2T1,则A、B两行星
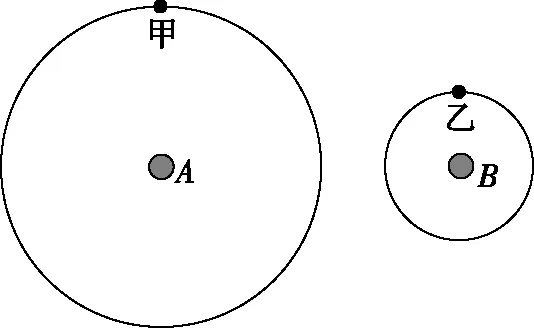
图14
( )
A.质量之比为1∶2
B.密度之比为32∶1
C.表面重力加速度大小之比为2∶1
【答案】BD
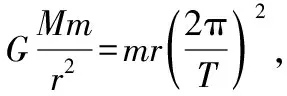
【点评】高考试题常将前几年考过的模型改编后再次进行考查,所以将高考题改编后进行训练很有必要。本题将2013年广东卷的一多中心天体问题进行了改编,从定性问题改编成了定量问题,改编1从一个角度进行了定量考查,改编2从四个角度进行了定量考查,试题难度比改编1增大不少,这也是控制选择题难度的一种常用方法。
五、逆向转换法、设问改变法
逆向转换法改编试题最典型的例子是利用光路可逆,将出射光线改为入射光线;设问换法改编试题通常是改变试题条件,从新的角度对试题进行设问编制。
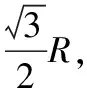

图15
(1)玻璃砖对光的折射率;
(2)截面圆弧上没有光射出部分的弧所对的弦长。
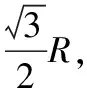

图16
(1)半球形玻璃砖对该单色光的折射率;
(2)光从C点传到B点所用的时间。
【解析】(1)光路如图17所示

图17
由几何关系知,在C点的入射角和折射角分别为
α=60°,β=30°

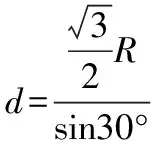
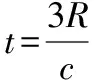
【点评】本题的命题意图是考查在光的折射中,求介质的折射率和光介质中的传播时间,因此笔者利用光路可逆对原题进行了改编,并增加了精密光学仪器这一科技情境,第1问题与原题设问相同,第2问设问角度则与原题不同,属于设问改变的试题改编方法。
六、试题改编的难度调整
试题改编要根据教学阶段和学生水平对试题难度进行把控,通常通过调整以下六个方面达到控制试题难度的要求。
笔者曾根据学生的水平差异,命制了三套平行的试题,下面是其中的一道试题。
【改编1】如图18所示,倾角为θ=37°的固定斜面长L=12 m,甲、乙两物块分别同时从斜面的顶端和斜面中点位置由静止释放,两物块恰好在斜面底端相遇。已知物块甲光滑,甲、乙两物块均可视为质点,sin37°=0.6,cos37°=0.8,重力加速度g取10 m/s2,求:
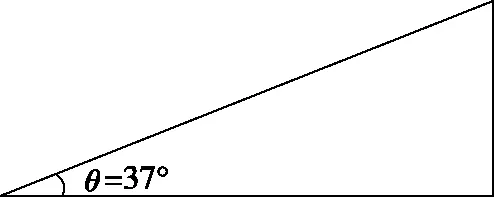
图18
(1)物块乙与斜面间的动摩擦因数。
(2)甲、乙两物块到达斜面底端时的速度大小分别为多少?
【解析】(1)对甲、乙两物块,分别应用牛顿第二定律,可得
m1gsinθ=m1a1
m2gsinθ-μm2gcosθ=m2a2
由运动学位移公式得
联立解得μ=0.375
(2)由运动学速度公式得
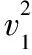
联立解得v1=12 m/s,v2=6 m/s
【改编2】如图19所示,固定在水平面上的倾角为θ=37°的斜面,斜面长L=6 m,物块甲以某一初速度从斜面底端沿斜面向上运动的同时,物块乙从斜面的顶端由静止释放,物块甲在斜面上运动到最高点时恰好与物块乙相遇。已知甲、乙两物块均可视为质点,且二者与斜面间的动摩擦因数均为μ=0.5,sin37°=0.6,cos37°=0.8,重力加速度g取10 m/s2,求:
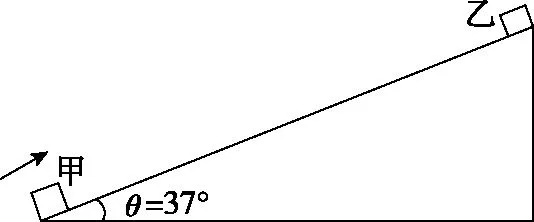
图19
(1)物块甲、乙相遇前的加速度大小分别为多少?
(2)物块甲的初速度大小和相遇时物块乙的速度大小。
【解析】(1)对甲、乙两小物块分别应用牛顿第二定律,可得
m1gsinθ+μm1gcosθ=m1a1
m2gsinθ-μm2gcosθ=m2a2
解得a1=10 m/s2,a2=2 m/s2
(2)由运动学位移公式得
又L=L1+L2
联立解得t=1 s
物块甲的初速度大小为v0=a1t=10 m/s
相遇时物块乙的速度大小v2=a2t=2 m/s
【改编3】如图20所示,倾角为θ=37°的固定斜面长L=7 m,物块甲以初速度v0=10 m/s从斜面底端沿斜面向上运动的同时,物块乙从斜面的顶端由静止释放,已知甲、乙两物块均可视为质点,且二者与斜面间的动摩擦因数均为μ=0.5,sin37°=0.6,cos37°=0.8,重力加速度g取10 m/s2。

图20
(1)通过计算,判断物块甲在沿斜面向上运动过程中,甲、乙两物块能否相遇。
(2)若甲、乙两物块能相遇,则二者相遇的位置离斜面底端的距离为多少?
【解析】(1)物块甲沿斜面向上运动的过程中,对甲、乙两物块,分别应用牛顿第二定律得
m1gsinθ+μm1gcosθ=m1a1
m2gsinθ-μm2gcosθ=m2a2
解得a1=10 m/s2,a2=2 m/s2
设物块甲沿斜面向上运动的时间为t1,由运动学位移公式得
v0=a1t1
联立解得L1+L2=6 m 则在物块甲沿斜面向上运动的过程中,甲、乙两物块没有相遇 (2)物块甲沿斜面向上运动到最高点后,再沿斜面向下运动过程中,由牛顿第二定律得 m1gsinθ-μm1gcosθ=m1a3 解得a3=2 m/s2 经时间t1物块乙的速度大小为v2=a2t1 若两物块在物块甲沿斜面向下运动过程中相遇,有 联立解得t2=0.5 s 物块甲经时间t2沿斜面向下运动的距离为 则两物块相遇位置离斜面底端的距离为 ΔL=L1-L3 联立解得ΔL=4.75 m 【点评】改编后的三道试题的情境相同,但难度逐渐增大,以适用不同水平的学生,其中改编3增加了评价和开放性,考查学生的高阶思维能力。
——《势能》

