研究高考真题 提升核心素养——以一道“爪型”三角形的变式探究为例

四川 邓成兵

“爪型”三角形是指在给定的一个三角形中，连接一个顶点和对边上的任意一点构成的图形.“爪型”三角形问题主要考查直观想象、数学运算、数据分析、逻辑推理等数学核心素养.笔者就从“爪型”三角形的代数特征和几何特征出发，力求在解法上寻求最简洁的方法，总结解题规律，从整体上认识把握，做到有的放矢.

《普通高中数学课程标准(2017版2020年修订)》中指出，高中数学教学应该以发展学生数学核心素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质，达到学生用科学方法分析问题、解决问题，才有利于引导学生将其转化为自己的思维方式.高考真题承载着引领教学的功能，作为重要的教学素材，试题的价值一直被教师在教学中深入思考、充分挖掘，变式探究、类比深化，全方位探究高考题的相关性及同源性.

从2015年到2022年，全国每年高考均出现“爪型”三角形，其中以解答题形式出现理科5次、文科4次，填空题文理科均为5次，选择题文理科均出现1次(如下统计表所示).本文以2022·全国甲卷·16的探究、发现过程中，从解法探究，到变式推广，再到获得“爪型”三角形相关性质.整个过程可以说是顺应了提升学生的数学核心素养.现与大家分享、交流.

“爪型”三角形在近八年高考中的地位及难度分析

1.试题呈现与解法探究

【命题意图】本题是典型的“爪型”三角形问题，需要灵活应用正、余弦定理进行边角互化与基本不等式求解；从多维度多方面考查学生的数学运算、数据分析、逻辑推理、直观想象等数学核心素养，综合性较强.

【解法一】(利用两次余弦定理列方程求解，即代数法)

设BD=x，CD=2x，△ABC中，角A,B,C所对的边分别为a,b,c,

在△ACD中，b2=4x2+4-2·2x·2·cos60°，

可得,b2=4x2-4x+4，

在△ABD中，c2=x2+4-2·x·2·cos120°，

可得，c2=x2+2x+4，

【解法二】(利用平面向量坐标法求解，即几何法)

以D为坐标原点建立如图所示平面直角坐标系，

设BD=x(x>0)，

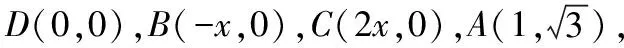
【解法三】(利用等面积法求解，即代数法)

设BD=x，CD=2x，如图，过顶点A作AE⊥BC于点E，

∵S△ABC=S△ABD+S△ACD，

则BE=x+1,CE=2x-1，

在Rt△ACE中，AC2=CE2+AE2=(2x-1)2+3=4x2-4x+4，

在Rt△ABE中，AB2=BE2+AE2=(x+1)2+3=x2+2x+4，

评析：解法一先算“两次”策略，依据余弦定理列方程求解，即代数方法，得到AC,AB两边关于x的关系式，再利用基本不等式进行求解；解法二建立直角坐标系，运用向量的模长公式得到AC,AB两边关于x的关系式，再运用基本不等式进行求解；解法三利用三角形的等面积法，得到AE的长度，结合直角三角形，利用勾股定理并结合基本不等式进行求解.解法三相对解法一和解法二，运算比较小，降低了运算量，在教学中，应该重视正余弦定理列方程组法、平面向量坐标法及等面积法在“爪型”三角形中的应用.

【解题思维导图】

解法一：

解法二：

解法三：

2.变式探究

【解法一】(算“两次”策略，依据正余弦定理列方程求解，即代数方法)

设BD=CD=m，AD=n，

在△ABD中，由余弦定理得c2=n2+m2-2×mn·cos∠ADB.①

在△ACD中，由余弦定理得

b2=n2+m2-2×mncos∠ADC.②

∵∠ADB+∠ADC=π，

∴cos∠ADB+cos∠ADC=0，

所以①+②，得b2+c2=2n2+2m2， ③

在△ABC中，由余弦定理得

4m2=b2+c2-2bccos∠BAC，

又∠BAC=120°，所以4m2=b2+c2+bc， ④

联立③④得，2b2+2c2-4n2=b2+c2+bc，

即b2+c2=bc+4n2≥2bc，

即bc≤4n2，当且仅当b=c=2n时，等号成立.

即AD=2.

【解法二】(用基底法对向量进行分解后平方转化为模长和数量积问题探究b,c间关系，即利用向量或坐标方法求解)

设AD=n,

∵D为BC的中点，

即b2+c2=bc+4n2，

而b2+c2≥2bc，

∴bc+4n2≥2bc即bc≤4n2，当且仅当b=c=2n时，等号成立，

即AD=2.

探究一类问题，形成结论

思考：把变式1中解法一③式中的m,n分别换成BD，AD，你会获得什么结论？

由①+②化简得，

∵D为BC的中点,

∴|BC|=2|BD|,代入③化简得,

【解法三】(结论应用)

设BD=CD=m，AD=n，

在△ABC中，利用余弦定理可得，

4m2=b2+c2-2bccos120°，化简得，

把②代入①化简得，

4n2+bc=b2+c2，

而b2+c2≥2bc，

∴bc+4n2≥2bc即bc≤4n2，

当且仅当b=c=2n时，等号成立，

即AD=2.

评析：解法一利用两次余弦定理，互为补角的两余弦值为零及基本不等式求解，难度较大，运算也比较大；解法二利用平面向量的中线公式，再运用基本不等式求解，运算较小,但难度较大；解法三与解法一和解法二比较，更加简便、高效，难度较小.本类题型侧重三角形的正余弦定理、诱导公式、三角形的面积公式、平面向量的中线公式及基本不等式，考查数形结合与化归转化思想，数学运算、逻辑推理等核心素养.

变式2：记△ABC的内角A,B,C的对边分别为a,b,c.若AD为∠BAC的平分线，交BC边于D点，AD=2,∠BAC=120°,求b+c的最小值.

【解法一】(等面积法求解，即代数方法)

由题意得，作出图象，如图所示.

设∠BAD=∠CAD=60°,∠BAC=120°，

∵S△ABC=S△ABD+S△ACD,

∵|AD|=2,

当且仅当b=c时,等号成立,

∴b+c的最小值为8.

探究一类问题，形成结论

结论2.由(*)化简得“爪型”三角形的角平分线公式：在△ABC中,∠BAC的平分线AD与BC边相交于点D，设∠BAD=∠CAD=θ,则∠BAC=2θ，则角平分线长度|AD|=

【解法二】(结论应用)

∴b+c的最小值为8.

评析：角平分线型侧重正余弦定理、三角形面积公式、两角和差的三角公式、二倍角公式、三角函数的性质以及角平分线定理的应用.解法一运用了三角形的等面积法及基本不等式的乘“1”法求解，学生难以想到，难度较大；解法二直接运用“爪型”三角形的角平分线公式及基本不等式的乘“1”法求解，难度较小，学生容易想到，考查逻辑推理能力、直观想象、数学运算、数学建模等核心素养.

思考：若点D不是角平分线与BC边的交点，为BC边上任意一点，也有相似的结论吗？

【分析】在三角形中出现了边和角的正弦，运用S△ABC=S△ABD+S△ACD，利用三角形面积的第二公式得证.

证明：∵S△ABC=S△ABD+S△ACD,

sinβ,

两边同时除以bc×|AD|,化简得,

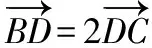
【解题思路】(用向量或坐标方法求解)

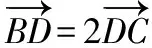
∵|AD|=2，∠BAC=120°,

解得bc≤18，

评析：由此解法中的(*)可得一般情况下爪型三角形的向量表示.

证明：∵|BD|=m,|DC|=n,

变式4：记△ABC的内角A,B,C的对边分别为a,b,c.若AD⊥BC，交BC边于D点,∠BAC=120°，AD=2,S△ABC的最小值为.

【解题思路】(等面积法和余弦定理求解)

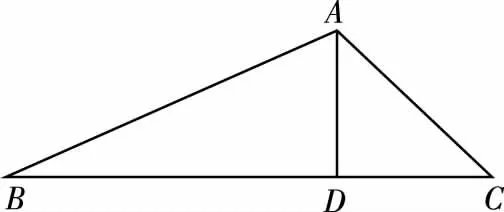
在△ABC中，a2=b2+c2-2bc×cos120°,

∴bc≥16,

评析：该类题目侧重直角三角形中互余两角的三角函数关系及两角和差的三角公式的应用.考查数学运算、数据分析、直观想象等核心素养.

每年高考真题都有源自于教材的例习题改编或组合，重在考查学生的基本知识、基本思想和基本技能，对学生的思维量、灵活性、数学核心素养提出较高要求.本题源于人教A版必修四第147页A组第13题改编，如变式5.

变式5：如图所示，l1,l2,l3是同一平面内的三条平行直线，l1与l2间的距离是1，l2与l3间的距离是2，正三角形ABC的三顶点分别在l1，l2，l3上，则△ABC的边长是________.

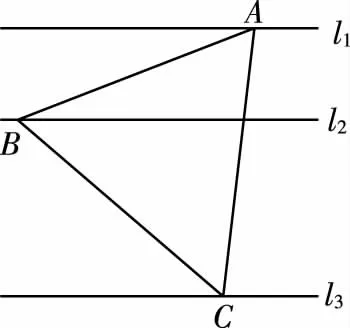
【解题思路】(正弦定理和三角形两角和与差公式求解)

设AC与l2交于D,设∠BDA=θ，∠DBA=β，设正三角形ABC的边长为a，

两式相除化简得，2sinβ=sin(60°-β),

评析：该类题目侧重三角形面积公式、两角和与差公式、二倍角公式、正余弦定理及其应用，考查逻辑推理、直观想象、数学运算等核心素养.

3.方法反思和素养展现

文章以2022年全国甲卷文理科第16题及变式,用不同的方法对“爪型”三角形进行了深入探究，归纳出“爪型”三角形的中线、角平分线、高线常规解法及相关二手结论并对其证明；运用了特殊到一般的数学思想、化归与转化思想、函数与方程等思想；“爪型”三角形在高考试卷中属于难度中等，解这类三角形方法很多，通常可以采用“邻补角策略”“算两次”策略依据正余弦定理列方程求解；也可以采用作高、作平行线等手段利用初等几何知识求解；亦可借助向量工具采用基底法对向量进行求解.但如果运用本文总结的爪型三角形的四条性质求解，不但可以简化我们的运算，还可以提高做题的速度及正确率.