例谈三角函数中ω的取值范围问题——基于核心素养的高考复习微专题

陕西 侯有岐

在近几年的高考中，三角函数是高考必考的重点内容，根据三角函数相关性质求解参数ω的值或取值范围是三角函数中比较典型的一类问题，它能有效考查学生对三角函数基本性质的掌握程度，因此备受高考命题者的青睐，但仍有部分学生对此类问题处理起来存在一定的困难，不知道如何等价转化问题的已知条件，造成求解范围不准确.本文就如何突破解析式中参数ω的策略作了一些总结，以供读者参考.

题型一：与函数的单调性有关

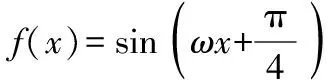
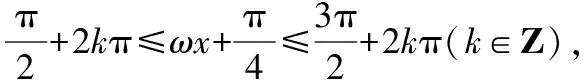
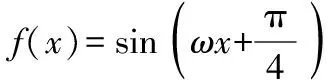
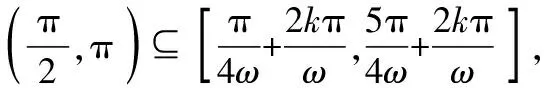
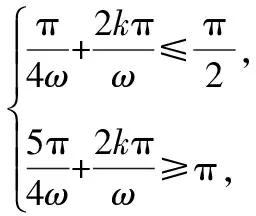
(2)已知三角函数f(x)=Asin(ωx+φ)(A>0,ω>0)在某个区间M上的单调性，求参数ω的取值范围，可先求出f(x)的同类单调区间D，然后利用M⊆D这个关系求解，如解法二，考查了部分与整体的思想；当然本题也可以利用导数知识解决，如解法一，考查了转化与化归的思想.

题型二：与函数的值域有关

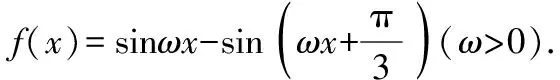
题型三：与函数的最值、极值有关

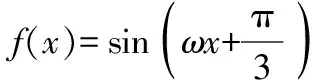
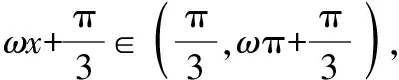
要使函数在区间(0,π)恰有三个极值点、两个零点，

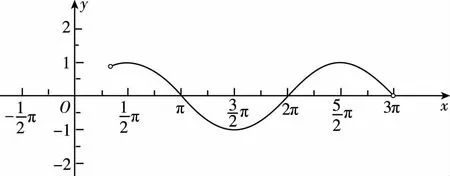
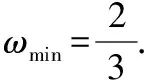
题型四：与函数的零点有关

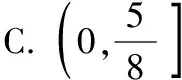
因为ω>0，当x∈(π,2π)时，

进而可得

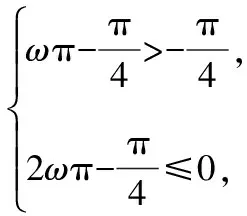
假设f(x)在区间(π,2π)内有零点，

点评：(1)三角函数y=Asin(ωx+φ)(A>0,ω>0)相邻两个零点间的距离的大小对函数周期的影响，也是求三角函数周期和参数ω的重要思路，但求解过程中应注意图象的平衡位置发生变化时，即平衡位置不在x轴上时，其相邻两个零点的距离一定不再是半个周期.

(2)本题解法二先假设在区间(π,2π)内有零点，然后分类讨论求出ω的范围，从而得出没有零点时ω的范围，即“正难则反”，考查了分类与整合的思想.

题型五：与函数的对称性有关

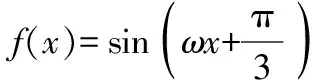
题型六：与函数的周期性有关

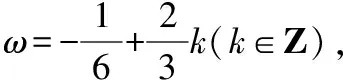
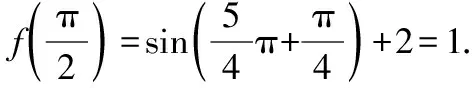
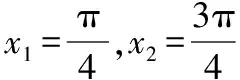
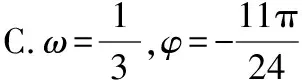
设f(x)的最小正周期为T，

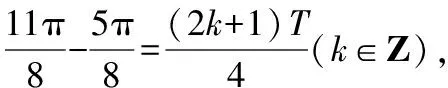
又f(x)的最小正周期大于2π,所以0<ω<1，

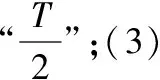
题型七：与函数的多种性质有关

A.11 B.9 C.7 D.5

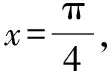
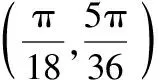
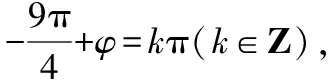
点评：三角函数的性质包含值域、最值、单调性、周期性、对称性和零点等多类性质，这些性质直接影响着函数周期的变化，也影响着参数ω的取值或范围，以上两个问题的解决都是着眼于三角函数的相关性质对函数周期的影响这一本质，考查了数形结合和转化与化归的数学思想.

结语：y=Asin(ωx+φ)的图象源于y=sinx，y=Acos(ωx+φ)的图象源于y=cosx，y=Atan(ωx+φ)的图象源于y=tanx，无论题目的背景换成什么，其本质不变，都是通过正弦函数、余弦函数、正切函数的图象和性质来解决，因此，借助三角函数的性质求解函数解析式中的参数ω，应在熟悉基本三角函数图象的基础上，通过掌握参数ω与三角函数的周期性、单调性、对称性和最值等之间的密切联系，利用整体思想和数形结合等数学思想，把复杂问题简单化、熟悉化，才能更有效地破解求参数ω过程中的难点.