指向直观想象素养阶段性评价的区域备考探索——以高考复习阶段中的立体几何题为例

湖北 周 威

1 基于立体几何命题，聚焦直观想象素养阶段性评价

直观想象是数学学科核心素养之一，《普通高中数学课程标准(2017年版2020年修订)》(以下简称课标)对直观想象素养的描述为借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养.课标指出，数学学科核心素养的发展具有连续性和阶段性.因此，高考复习备考需要关注核心素养的阶段性发展和评价.在高考和各种模拟考试中,学生直观想象素养的阶段性评价可以从立体几何试题的命题设计、考试结果以及问题的变式或一题多解等方面来体现，那么如何来呈现这种阶段性发展和阶段性评价呢？笔者以为，可以以高三复习备考中的一、二轮复习阶段作为研究对象，分别以两阶段复习中的两次区域联考作为监测工具，首先从高考命题规律中把握必备知识、关键能力的考查要求；其次是确定学生的一轮复习阶段现有水平以及经过一轮复习后学生可能达到的发展水平；最后是通过同类型必备知识的问题变式或一题多解，提升学生不同复习阶段的直观想象素养水平.因此，笔者接下来将从这一角度阐述直观想象素养在一、二轮复习备考阶段的发展和评价.

统计近几年立体几何大题考点不难发现,高考中的立体几何解答题以学生所熟知的空间几何体为载体，采用“证明+计算”的设问方式(即第(1)问主要考查点、线、面位置关系的证明，第(2)问考查空间角、体积的计算)，突出基础知识，注重数形结合、化归与转化等数学思想方法，对培养学生直观想象素养有积极意义.因此，对于本届高三的学生，两次区域联考立体几何题都定位于19题位置，必备知识和关键能力可设置如下表，并都确定为数学探究问题.

表1 两次区域联考立体几何题双向细目表

2 基于四棱锥模型，体现两轮复习阶段直观想象水平

四棱锥模型是高考中的常规模型，一般考查其底面为平行四边形或为梯形的情形.因此，第一轮复习阶段的区域联考立体几何题可以将四棱锥模型底面设置为梯形，第一问考查线面垂直的证明方法，定位基础题；第二问考查是否存在点使得面面垂直的数学探究问题，定位常规而又不乏味的中档题.第二轮复习阶段的区域联考可以将底面设置为平行四边形，第一问考查面面垂直的证明方法，同样定位基础题；第二问考查面与面不垂直的情形下，已知二面角寻找点的位置的数学探究问题.因此，两次区域联考命题意图类似、考点类似、证明或计算方法类似，可以更好地反映出学生两轮复习阶段的实际水平.

2.1 一轮复习阶段学生直观想象水平描述

【例1】(恩施州2022届高三第一次质检·19)如图所示，在四棱锥P-ABCD中，PA⊥平面ABCD,AB⊥AD,AB∥CD,AB=AD=PA=2CD=4，G为PD的中点.

(1)求证：AG⊥平面PCD;

(2)若点F为PB的中点，线段PC上是否存在一点H，使得平面GHF⊥平面PCD？若存在，请确定H的位置；若不存在，请说明理由.

解：(1)证明：因为PA⊥平面ABCD,AB⊂平面ABCD，所以PA⊥AB.

又AD⊥AB,DA∩PA=A，所以AB⊥平面PAD,

又AB∥CD,所以CD⊥平面PAD.

又AG⊂平面PAD,所以CD⊥AG.

又PA=AD,G为PD的中点，所以AG⊥PD,PD∩DC=D,所以AG⊥平面PCD.

(2)以A为坐标原点，AD,AB，AP所在直线建立如图所示的空间直角坐标系，

则A(0,0,0),C(4,2,0),P(0,0,4),F(0,2,2),G(2,0,2)，

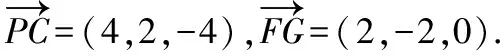
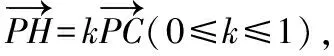
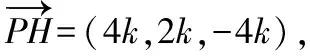
设平面GHF的法向量为n=(x,y,z),

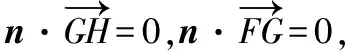
可取n=(2k-1,2k-1,3k-1)，

水平描述：此题均分3.9分，难度系数0.33，区分度0.74.从难度系数看，是属于中档偏难题.学生答题主要是通过向量坐标法.课标对“立体几何”部分的学业要求为：能够运用图形的概念描述图形的基本关系和基本结果.能够证明简单的几何命题(平行、垂直的性质定理)，并会进行简单应用.与学业要求对比，出现的问题如下：首先，学生不能用符号语言准确表达线线关系、线面关系及面面关系;其次，应用中学生解决问题方法单一，计算能力较差，解决实际问题能力不足.因此，在以后的复习中注重符号语言的表达、书写规范，要注重引导学生一题多解，从不同的角度分析问题，加强对学生“解决数学问题”能力的培养.

2.2 二轮复习阶段学生直观想象水平描述

【例2】(恩施州2022届高三第二次质检·19)如图所示，在四棱锥P-ABCD中，底面ABCD为正方形，PA⊥底面ABCD，PA=AB，两点E，F分别为线段PB，BC上的动点.

(1)若E为线段PB的中点，求证：平面AEF⊥平面PBC；

解:(1)证明:由PA⊥底面ABCD，BC⊂平面ABC,可得PA⊥BC.又在正方形ABCD中，BC⊥AB，且PA∩AB=A，则BC⊥平面PAB.又AE⊂平面PAB，有BC⊥AE.

由PA=AB，E为PB中点，可得AE⊥PB.

又PB∩BC=B，则AE⊥平面PBC.又AE⊂平面AEF，从而平面AEF⊥平面PBC.

(2)如图所示，以A为坐标原点，AB,AD,AP所在直线分别为x，y，z轴，建立如图所示的空间直角坐标系.

设平面AEF的法向量为n=(x,y,z)，

取y=1，则x=-λ，z=1-λ，即n=(-λ,1,1-λ).

水平描述:此题区域均分4.9分，难度系数0.41，区分度0.7.从难度系数看，对于区域内学生来说，依然属于中档偏难题，第一问“几何关系的证明”得分得到了提升，这说明一定程度上，学生对“几何直观和空间想象感知事物的形态与变化”理解增强，然而对比课标“学业要求”，出现的问题依然有：学生对垂直部分的判定定理和性质定理的转化能力弱、长度关系的符号语言与点线面位置关系的图形语言转化能力不够；第二问大部分学生都基本能采用向量坐标方法建立空间直角坐标系，运用合适的向量模型，将相对困难的逻辑推理问题转化为向量运算来解决，直观想象素养得到了提升，但依然计算能力差.这也说明直观想象素养并不是孤立的，直观想象素养的提升与逻辑推理、数学运算等素养密切相关.

与学生一轮复习阶段直观想象水平比较，区域均分有小幅度提升，针对历年高考得分情况，进步是明显的.出现的问题依然是数学符号语言的描述不够严谨和准确；在数学运算方面，计算能力依然较差.这说明，在学生直观想象水平发展的过程中，不仅要关注学生对知识技能掌握的程度，还要更多地关注学生的思维过程，判断学生是否会用数学的眼光观察世界，是否会用数学的思维思考世界，是否会用数学的语言表达世界.因此，以后的立体几何复习阶段，要加强将数学语言表达能力提升和数学运算能力提升融入到不同的解题策略当中.

2.3从不同解题策略提升直观想象素养

立体几何中常见的解法包括空间向量坐标法、基向量法、几何法、补形法(融入立体几何模型)、投影面积法等，除了空间向量坐标法，其他解法也能很好地考查空间想象能力，提升理性思维能力，这就是“一题多解”的好处.因此，解法的多样性十分有助于提升学生直观想象水平，既能展现学生数学学习过程中思维品质的形成过程，又体现了学生在具体的问题情境中，结合个人实际、灵活选择方法、应用数学能力的过程.

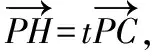
如图，作HH′⊥PA于点H′，QQ′⊥PA于点Q′.

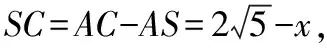
【例2】解法2(几何法)：设M为PB的中点，如图所示，当E在线段PM上时，过PB的中点M作MH⊥EF，连接AH.易知AM⊥平面PBC，EF⊂平面PBC,可得AM⊥EF.又MH∩AM=M，则EF⊥平面AMH，从而可知∠AHM为平面AEF与平面PBC所成夹角.

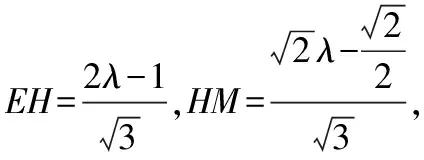
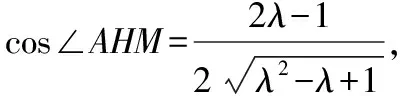
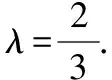
综上，可知F为BC的三分点.

【例2】解法3(投影面积法)：设M为PB的中点，如图所示，当E在线段PM上时，连接AM与MF，易知AM⊥平面PBC，可得△MEF为△AEF在平面PBC中的投影.

设AB=1，BF=λBC=λ.

在△AEF中，

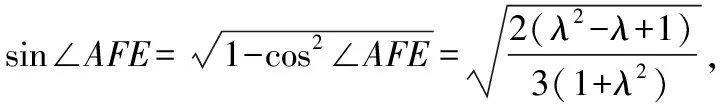
设θ为平面AEF与平面PBC的夹角，

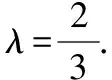
3 结语