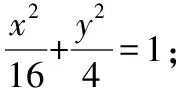顺应“三新”研究趋势 探索变式教学模式——“数学经典试题及变式”征集活动解析几何题组精选

一、直线与圆锥曲线的位置关系

【甘肃 彭长军】

(1)求l的斜率；

【试题分析】考查知识：点、直线与双曲线的位置关系，斜率公式、弦长公式以及二倍角正切公式等；解题方法：常规方法、化归与转化思想的应用；综合拓展：直线与圆锥曲线的位置关系的综合问题.

【解题策略】充分利用已知条件并结合相关知识用常规方法求解，相应解题步骤的思维导图如下：

思路1--根据已知条件确定a后写出双曲线C的方程，在此基础上，将直线l的方程设为y=kx+m.--将直线l的方程与双曲线C的方程联立消去y得到关于x的二次方程，利用根与系数的关系及斜率公式可求得直线AP和AQ的斜率之和；接着利用第(1)小问的结论及第(2)小问的条件可求出弦PQ的长及点A到直线l的距离，进而利用三角形面积公式求得结果.

思路2--在确定双曲线C的方程后可将直线AP的方程设为点斜式，将其代入双曲线C的方程，得到一个关于x的二次方程，利用根与系数的关系及点A的横坐标为2可表示出xp，进而可表示出yp,进而可得直线AB的参数方程.--将xp,yp中的k换成-k便可表示出xQ,yQ,进而利用斜率公式可求得直线AP和AQ的斜率之和；接着利用第(1)小问的结论及第(2)小问的条件可求出直线AP的斜率，进而可求得P,Q两点的坐标，利用两点间的距离公式求得|AP|,|AQ|，再由三角函数知识可求得sin∠PAQ，最后利用面积公式可求得结果.

【解法1】点拨：常规方法求解——从直线l入手，利用根与系数的关系及弦长公式等求解

(1)设直线l的方程为y=kx+m，将其代入x2-2y2-2=0，得(1-2k2)x2-4mkx-2m2-2=0(1-2k2≠0),

由直线l与双曲线C相交于P,Q两点，知Δ>0，

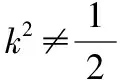
设P(x1,y1)，Q(x2,y2)，

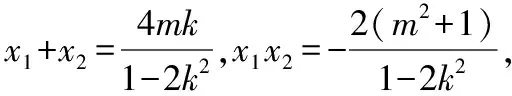
亦即(x2-2)(kx1+m-1)+(x1-2)(kx2+m-1)=0，

化简整理，得

2kx1x2+(m-2k-1)(x1+x2)-4(m-1)=0. ②

将①代入②并化简整理，得(k+1)(2k+m-1)=0，

当2k+m-1=0时，m=1-2k，此时直线l的方程为y=k(x-2)+1，直线l过点A(2,1),与是没不符.

∴k+1=0，即k=-1.

(2)当k=-1时，x1+x2=4m，x1x2=2(m2+1)，且m2>1，

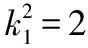
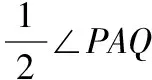
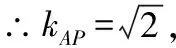
由点P(x1,y1)在直线l上，得y1=-x1+m.③

又直线AP的方程为y-1=k1(x-2)，

∴y1-1=k1(x1-2), ④

由③④，得m=(k1+1)x1+1-2k1, ⑤

同理可得m=(-k1+1)x2+1+2k1. ⑥

∴(x2-x1)2=32(m-1)2，

即(x2+x1)2-4x1x2=32(m-1)2，

∴16m2-8(m2+1)=32(m-1)2，

化简整理，得3m2-8m+5=0，

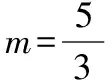
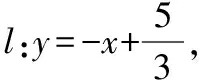
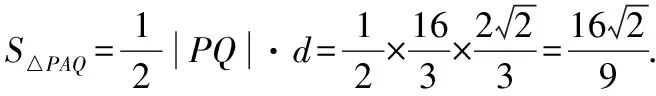
【解法2】点拨：常规方法求解——从直线AP入手，利用根与系数的关系及两点间的距离公式等求解

(1)设直线AP的斜率为k，则直线AQ的斜率为-k.

于是直线AP的方程为y-1=k(x-2)，

即y=kx+(1-2k)，将其代入x2-2y2-2=0，

得(2k2-1)x2+4k(1-2k)x+4(2k2-2k+1)=0，

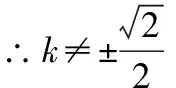
(2)若直线AP的斜率为k(k≠-1,否则A，P，Q三点共线)，则直线AQ的斜率为-k.

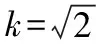
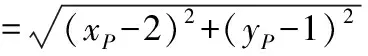
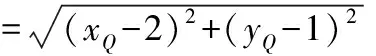
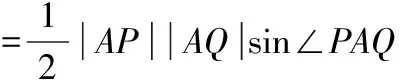
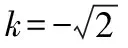
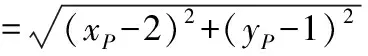
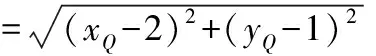
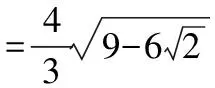
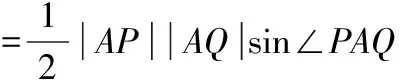
【点评】1.解法1虽然容易上手，但过程繁杂，有些地方不易想到，如在确定斜率的值时，对2k+m-1=0的讨论，又如在确定m的值时，过程复杂且不易想到.解法2不易上手，但过程比解法1简单且运算量小.

2.△PAQ的面积也可用向量的数量积求得，即

【甘肃 彭长军】

【变式1】(知识变式)对调条件与结论并对结论加以应用

(1)求直线AP,AQ的斜率之和；

(2)若△APQ是等边三角形，求直线l的方程及直线AP的斜率.

【答案】(1)0；

【河北 赵伟娜】

【变式2】(方法变式)以圆的切线形式给出两直线斜率互为相反数信息，求直线方程

(2021·八省市联考·7)已知抛物线y2=2px(p>0)上三点A(2，2)，B，C，直线AB，AC是圆(x-2)2+y2=1的两条切线，则直线BC的方程为

( )

A.x+2y+1=0 B.3x+6y+4=0

C.2x+6y+3=0 D.x+3y+2=0

【答案】B

【广东 黄威】

【变式3】(综合变式)由kAP+kBP=λ(λ≠0)推广到kAP×kBP=λ(λ≠0)

【答案】(6,-3)

【贵州 李寒】

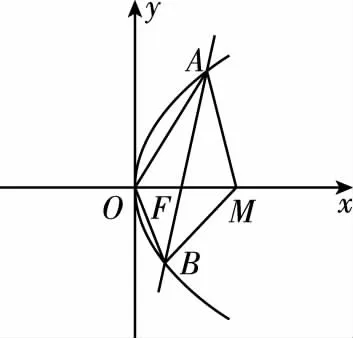
【母题2】(2022·全国新高考Ⅱ卷·10)已知O为坐标原点，过抛物线C：y2=2px(p>0)的焦点F的直线与C交于A，B两点，点A在第一象限，点M(p,0)，若|AF|=|AM|，则

( )

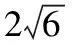
B.|OB|=|OF|

C.|AB|>4|OF|

D.∠OAM+∠OBM<180°

【试题分析】考查知识：抛物线的标准方程、几何性质，直线与抛物线的位置关系.

解题方法：数形结合，联立方程；运用定义和向量；综合素养：基于直线与抛物线的位置关系考查数学抽象、逻辑推理和直观想象等数学核心素养;

综合拓展：依据题设可知正确选项得到的结论具有一般性.

【解题策略】本题主要考查利用直线与抛物线的位置关系及应用，运用数形结合等方法来解决，落实基础性的考查.

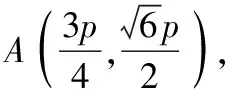
【方法总结】圆锥曲线问题的本质是把几何问题转化为代数问题，通过代数运算研究几何图形性质，图形问题代数化是解析几何的本质.求解圆锥曲线问题的关键在于找到最好的方法解决问题，注重回归定义、联立方程、数形结合利用几何性质，或利用向量知识等，相比用固定解题程序，能更快地找到简捷的解题方法.

【吉林 韩兆峰】

【变式1】(知识变式)由线段相等为垂直的变式

C.|AB|<|OM| D.∠AOB>120°

【答案】ACD

【甘肃 董宏杰】

【变式2】(方法变式)侧重代数与几何方法对比，优化运算过程，提升学生数学素养

【答案】C

【吉林 韩兆峰】

【变式3】(综合变式)依据直线与圆锥曲线的关系确定直线方程的变式

设抛物线C：y2=4x的焦点为F，点D(2,0)，过F的直线交C于M，N两点.当直线MD垂直于x轴时，|MF|=3.若直线MD,ND与C的另一个交点分别为A，B，记直线MN,AB的倾斜角分别为α,β.当α-β取得最大值时，直线AB的方程是________.

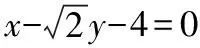
二、圆锥曲线中范围与最值问题

【江西 叶新波 叶军水】

【母题】(2022·全国甲卷文·21)设抛物线C：y2=2px(p>0)的焦点为F，点D(p,0)，过F的直线交C于M，N两点.当直线MD垂直于x轴时，|MF|=3.

(1)求C的方程；

(2)设直线MD,ND与C的另一个交点分别为A，B，记直线MN,AB的倾斜角分别为α,β.当α-β取得最大值时，求直线AB的方程.

【试题分析】考查知识：焦半径公式，求抛物线方程，直线与圆锥曲线，函数最值;

解题方法：数形结合，函数与方程，化归与转化

综合拓展：角度差量最值转化为斜率最值，利用函数处理最值问题.

【解题策略】

(1)焦半径公式→p→抛物线方程;

(2)画出图象→讨论MN斜率不存在→k存在设点，设线，得出y1与y3，y2与y4的关系→利用倾斜角与斜率的关系得出tan(α-β)→将直线与抛物线联立获得关于m的式子→利用函数处理最值→得出直线AB方程;

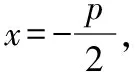
所以抛物线C的方程为y2=4x.

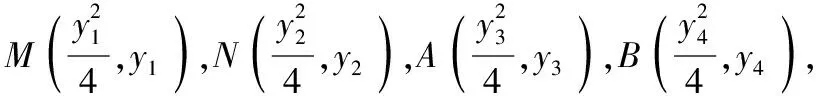
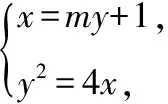
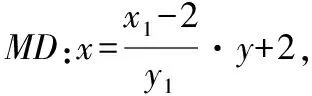
Δ>0,y1y3=-8，所以y3=2y2，同理可得y4=2y1，

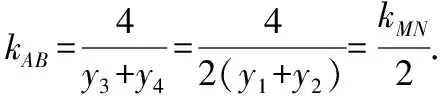
又因为直线MN，AB的倾斜角分别为α,β，

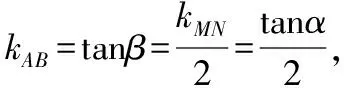
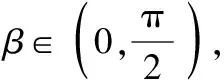
设kMN=2kAB=2k>0，

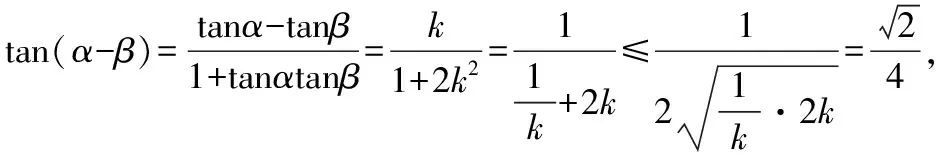
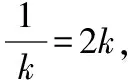
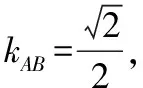
Δ>0，y3y4=-4n=4y1y2=-16,所以n=4，

【方法总结】此题在2010年的四川初赛试题定值的基础上增加了求最值，掩盖定值，增强了问题的探究性，是一道优秀的压轴题改编样本.角度差量最值转化为斜率最值，综合利用联立代换转化等综合方法，考查学生运算能力，分析问题，解决问题的能力，是一道不可多得的优秀压轴题.

【江西 叶新波】

【变式1】(知识变式)描述命题背景分析，二次曲线中的蝴蝶定理

(1)求椭圆C的标准方程；

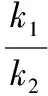
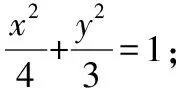
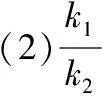
【江西 叶新波】

【变式2】(综合变式)在母题考查的基本知识与基本方法基础上，增加一条直线斜率，通过三个斜率等量关系，得出参数值，再根据直线与圆锥曲线联立得出直线方程

(1)求椭圆C的方程；

(2)过点Q(2,0)的直线l1与C交于M，N两点，点R是直线l2：x=m上任意一点，设直线RM,RQ,RN的斜率分别为k1,k2,k3，若k1+k3=2k2，求l2的方程.