例谈高中数学中的因式分解教学

安徽 李永林 刘 群

把一个多项式化为几个整式的积的形式，叫做因式分解,也叫做把这个多项式分解因式.高中阶段，因式分解在解决有关“函数零点”“函数极(最)值”“函数单调性”“多字母方程”“不等式”等方面问题的过程中起着关键性的作用.数学运算是高中阶段的主要数学核心素养之一，运算能力也是初中阶段的数学核心素养的主要表现之一，因式分解是一类代数式的运算，教师应在实际教学中高度重视这部分内容.

1 问题的发现与提出

《义务教育数学课程标准(2022年版)》规定：能用提公因式法、公式法(直接利用公式不超过二次)进行因式分解(指数是正整数).对于分组法，仅略有涉及.《普通高中数学课程标准(2017版2020年修订)》仅在一处用到了“因式分解”这个词语，对因式分解更没有具体要求.不难看出，对于因式分解，初中教学要求不高，高中又没有深化，很多学生在应对函数零点、极(最)值、单调性、多字母方程及不等式中涉及的略为复杂的因式分解时，感到束手无策，最终导致解题失败.在高中阶段，如何深化因式分解教学，凸显因式分解的解题价值呢？这是值得且应该思考的问题.

2 问题的分析与解决

2.1 深化因式分解的方法

因式分解常用的方法有提公因式法、公式法、分组分解法、十字相乘法、求根法、特殊值法、拆项法、待定系数法、除式法等，高中应深化十字相乘法、拆项法、待定系数法、除式法的教学，从而能快速对一个式子进行因式分解.

2.1.1 拆项法

故利用拆项法进行因式分解得x3-2x-4=x3-4x+2x-4=(x-2)(x2+2x+2)，

令h(x)=x2+2x+2-2ex，

则h′(x)=2x+2-2ex，

令m(x)=h′(x)，则m′(x)=2-2ex<0(x>0)，

点评:分离参数,再利用导数求最值是处理不等式恒成立问题的一个通法，因式分解是破解函数极(最)值点问题的利器.这里利用拆项法(将-2x拆成-4x与2x的和)对三次多项式x3-2x-4进行了因式分解，也是顺利解决此问题的关键.事实上，针对x3-2x-4的因式分解，还有如下方法.

另一种拆项法：

x3-2x-4=x3-8-2x+4=(x-2)(x2+2x+4)-2(x-2)=(x-2)(x2+2x+2).

2.1.2 待定系数法

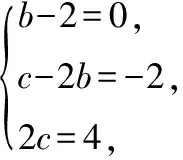
所以x3-2x-4=(x-2)(x2+2x+2).

2.1.3 除式法

以上三种方法的前提是知道x-2是多项式x3-2x-4的一个因式.如何找到这个因式？我们可以作如下思考：若一个多项式f(x)可分解成n个因式f1(x)，f2(x)，f3(x)…fn(x)，即f(x)=f1(x)·f2(x)·f3(x)·…·fn(x),根据多项式乘法法则，不难得到多项式f(x)的常数项等于各因式中的常数项的积，多项式f(x)的最高次项系数等于各因式中最高次项系数的积.如果多项式f(x)的最高次项系数为1，则该多项式可以分解成若干个最高次项系数为1的因式，于是，可通过对多项式f(x)的常数项进行整因数分解去寻找f(x)的一次因式.

2.1.4 十字相乘法

十字相乘法：对于一个二次三项式，若存在这样一个十字“×”，十字左边两数相乘等于二次项系数,右边两数相乘等于常数项,交叉相乘再相加等于一次项系数，那么左边两数和右边两数分别为两个因式的一次项系数和常数项.对于十字相乘法，大家都比较熟悉，这里不再举例赘述.

2.2 强化因式分解的应用

【例2】因式分解x3-4x2-3x-10.

解析：(-5)×2=-10，尝试可以得到x-5是原多项式的一个因式，将-4x2拆成-5x2+x2，再分组分解即可.

x3-4x2-3x-10=(x-5)x2+(x-5)(x+2)

=(x-5)(x2+x+2).

点评：尝试得到因式x-5后，也可以利用待定系数法和除式法进行因式分解，方法多样.

【例3】因式分解e2x+e-2x-2aex-2ae-x+4a-2.

解析：将ex+e-x当作整体配方得，e2x+e-2x-2aex-2ae-x+4a-2=(ex+e-x)2-2a(ex+e-x)+4a-4，再利用十字相乘法得到(ex+e-x-2)(ex+e-x-2a+2).

点评：把ex+e-x当作整体对原式进行配方，再利用十字相乘法处理，简洁明了.

解析：此题sin2x，sinx，cosx共存，利用换元法或导数法很难处理，顺着展开后的式子采用局部因式分解得

点评：对展开后的式子进行局部因式分解，为均值不等式的利用创造条件.在均值不等式和辅助角公式的共同作用下，问题化繁为简.需分析两次等号能否同时取得，体现了数学的严谨性.

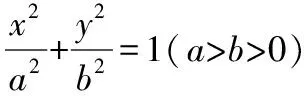
解析：①当BC⊥x轴时，

设直线AB的方程为y=x+a，

(b2+a2)x2+2a3x+a2(a2-b2)=0，

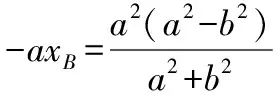
②当直线BC的斜率存在时，

设直线BC的方程为y=kx+t，B(x1,y1)，C(x2,y2)，

(b2+a2k2)x2+2a2ktx+a2(t2-b2)=0，它的两根分别为x1，x2,

代入化简得a4k2+a2t2+b2t2-a2b2k2-2a3kt=0,

分组分解得a4k2-2a3kt+a2t2+(b2t2-a2b2k2)=0，

进一步分解得(t-ak)(b2t+ab2k+a2t-a3k)=0,

当t=ak时，直线BC恒过顶点A(-a,0)(由①知，当BC⊥x轴时不符合)，舍去；

点评：因式分解是解决多字母方程的有效方法，多字母的代数式及其运算过程繁杂，因式分解后的结果简洁，便于计算，利于问题解决，体现了数学的奇妙.

3 结语