赏析函数性质的应用之美

李加军 马丽丽

(北京市第一0一中学怀柔分校,101407) (山东省潍坊市第七中学,261021)

2017年版《普通高中数学课程标准》明确指出，在学习数学和应用数学的过程中,学生能发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养.数学核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现,是在数学学习和应用的过程中逐步形成和发展的.六大数学核心素养既相对独立、又相互交融,构成一个有机的整体,集中体现数学课程目标,反映当前数学课程改革的主要方向和目标.

奇偶性、单调性、周期性、对称性是函数的常用的基本性质.在数学解题中,充分发现、分析、利用这些性质,既可以快速巧妙地解决问题,又可以感受到数学给人带来的魅力和愉悦,有助于提升学生的数学学科核心素养.

一、求函数值或最值

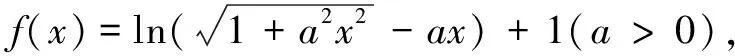
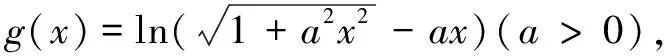
(A)8 (B)4 (C)-4 (D)-8

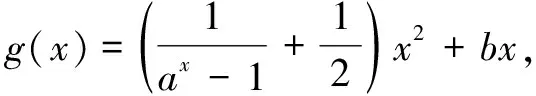
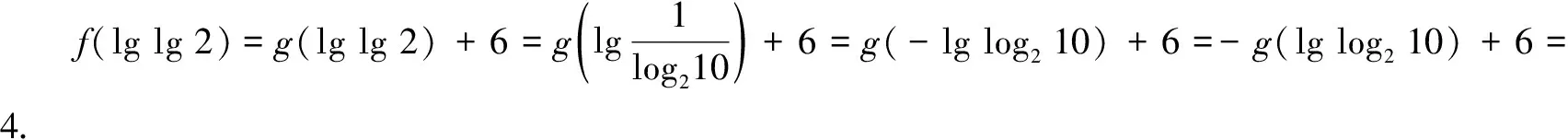
评注上述两题中f(x)满足f(x)=g(x)+c,其中g(x)是奇函数,c为常数,而所研究函数值对应的两个自变量互为相反数,利用奇函数g(x)满足g(x0)+g(-x0)=0,可知f(x0)+f(-x0)=2c.

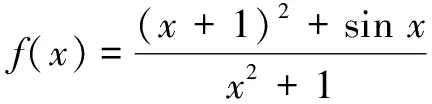
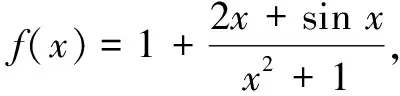
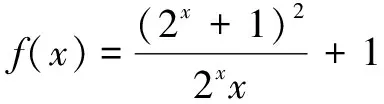
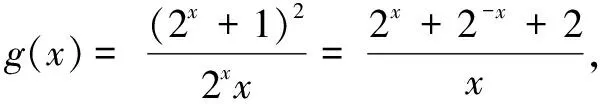
评注在上述两题中,从表面上看不易发现函数f(x)的性质,此时通过运算进行大胆合理的等价变形,使得f(x)满足f(x)=g(x)+c,其中g(x)是奇函数,c为常数,则根据奇函数g(x)满足gmax(x)+gmin(x)=0,可知fmax(x)+fmin(x)=2c.

二、求解方程

例5(2013年复旦大学自主招生题)已知ex=4-x,lnx=4-x的两个解分别是x1,x2,则x1+x2=______.

解令f(t)=et+t-4,则f(t)在R上是单调增函数.又ex1+x1-4=0 且lnx2+x2-4=0,即eln x2+lnx2-4=0,所以f(x1)=f(lnx2),有x1=lnx2,进而有x1+x2=x2+lnx2=4.

例6(2012年河南预赛题)若α是方程xex=2 011的解,β是方程xlnx=2 011 的解,则αβ=______.

解令f(t)=tet,易知f(t)=tet在(0,+∞)是单调增函数,由条件知αeα=2 011 且βlnβ=2 011,即αeα=2 011 且(lnβ)eln β=2 011,所以f(α)=f(lnβ),得α=lnβ,所以αβ=βlnβ=2 011.

评注在上述两题中,利用其中一个方程构造具有单调性的函数f(t),满足f(x1)=c.然后将另一个方程由运算(如取对数或指数)转化为满足f(h(x2))=c,再根据单调函数是一一映射的特点可得x1=h(x2),从而使研究问题得以解决.

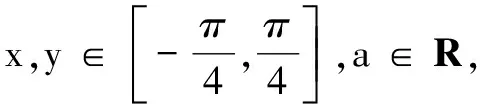
则cos(x+2y)=______.

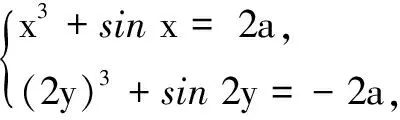
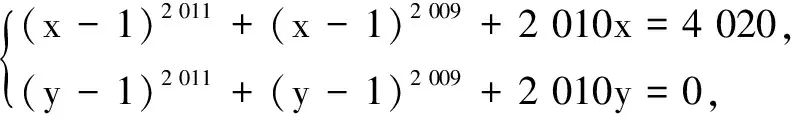
解由条件得

令f(t)=t2 011+t2 019+2 010t,则f(t)在R上单调递增且为奇函数.又f(x-1)=-f(y-1),所以f(x-1)=f(1-y),得x-1=1-y,即x+y=2.

评注在上述两题中,将两个方程经过变形构造出具有单调性和奇偶性的函数f(t),满足f(s)=c和f(t)=-c,于是f(s)=-f(t),得f(s)=f(-t),从而s=-t,问题可获解.

三、求函数值之和

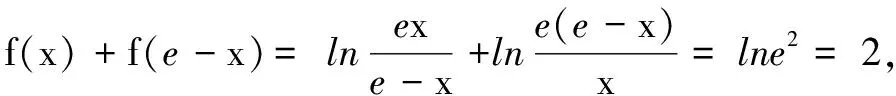
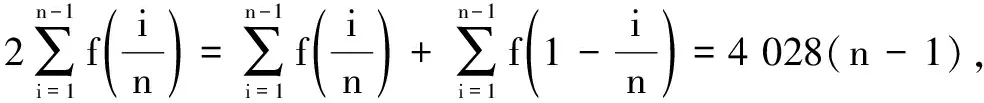
评注在上述两题中,观察结构易发现函数具有运算上的对偶性,即f(x)+f(s-x)=c,于是类比等差数列倒序求和取半的思想方法求得所要计算的结果.

四、求解不等式

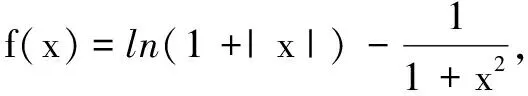
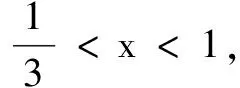
评注在上述两题中,观察结构易发现函数具有奇偶性,然后思考探究其单调性,使问题顺理成章得到解决.