基于对抗训练和图像去噪的对抗样本防御算法

刘斯杰，张志祥，张乔嘉

(1. 海军工程大学 电子工程学院，湖北 武汉 430033；2.海军工程大学 信息安全系，湖北 武汉 430033)

0 引 言

现如今的目标检测算法大多基于深度学习技术，而深度学习领域安全性问题主要来源于对抗样本的发现。Szegedy等提出对抗样本。研究员发现在一个图像样本上添加一些微小的扰动，会使得深度学习模型出现分类错误、检测准确率降低的问题[1]。随着Pedro等[2]以及Goodfellow等[3]对对抗样本的研究和推动，学术界对深度学习模型鲁棒性的研究走向了热潮。与对抗样本密切相关的对抗防御领域成为了研究热点。现有的对抗防御方法着重于对抗样本检测性防御技术和对抗样本鲁棒性防御技术两个方面。对抗样本鲁棒性防御技术主要着重于对抗训练[4,5]，将生成的对抗样本加入到原有训练集中进行训练，以此提高模型的鲁棒性。然而对抗训练后的模型在不同算法的攻击下，依然会找到新的对抗样本使模型失效。

本文将对抗样本检测性防御和对抗样本鲁棒性防御思想相结合，采用非局部均值去噪算法与对抗训练相结合，提出了NLM-AT(non-local means adversarial train)算法。该算法的思想为：以图像处理领域的非局部均值去噪算法为基础，NL-means算法是通过图像的上下文信息去噪，没有训练网络的数据、时间开销。样本输入网络前，先对其进行去噪，这样做会降低模型对正常样本的检测能力，提升其对对抗样本的检测能力；在对抗训练过程中，加入去噪后的正常样本和对抗样本，加强模型对去噪图像特征的学习。前者能解决对抗训练模型会被相同攻击算法攻击的问题，后者则可以解决去噪算法对正常样本检测的不良影响。通过检测性防御和鲁棒性防御的配合，在防御当前主流攻击算法上有较优异的效果。

1 相关工作

1.1 对抗攻击

现如今研究人员对对抗攻击算法进行了多方面的研究，对抗攻击算法在一级分类下可以分为：全像素攻击和部分像素攻击；在二级分类下可以分为：目标定向攻击和目标非定向攻击、黑盒攻击和白盒攻击、肉眼可见攻击和肉眼不可见攻击[6]。

FGSM(fast gradient sign method)是一种快速梯度符号法[3]，属于白盒攻击。通过计算模型对输入样本的导数，然后用符号函数得到其具体的梯度方向，接着乘以一个步长，就可以得到扰动噪声，将扰动噪声添加在原始样本上就得到了对抗样本。

I-FGSM(iterative fast gradient sign method)算法[7]在FGSM算法的基础上增加了迭代环节，在FGSM单步得到扰动后，会继续将扰动输入模型，然后重复FGSM算法的计算步骤，在多次迭代后得到攻击效果更好的对抗样本。通过这种方式生成的对抗样本的迁移性较差，对其它黑盒网络模型的攻击效果弱于FGSM。

PGD(projected gradient descent)算法[4]在I-FGSM的基础上增加了随机初始化的步骤，是此方法的变体，它用均匀的噪声作为初始化使得对抗样本具有更强的攻击性，并且模型对这种方法生成的对抗样本进行对抗训练后会具有更强的防御能力。

为了结合上述几种算法的白盒、黑盒攻击效果，让对抗样本在具有良好的白盒攻击效果下还有较强的迁移性，MI-FGSM(momentum iterative fast gradient sign method)算法[8]在I-FGSM算法的基础上增加了动量参数，基于动量的迭代来计算扰动。在计算梯度时通过添加动量参数能够有效跳出局部极值点，可以产生更具迁移性的对抗样本。

FGSM算法生成的对抗样本在白盒攻击条件下有一定的对抗性，I-FGSM、PGD生成的对抗样本在白盒攻击条件下有更强的对抗性，MI-FGSM算法生成的对抗样本有更强的迁移性，在白盒、黑盒攻击条件下均有一定的攻击效果。

1.2 对抗防御

2016年，HENDRYCKS等[9]提出了H&G对抗攻击检测技术，H&G技术是通过正常样本和对抗样本之间的数据差异来进行样本检测分类。

2017年，METZEN等[10]提出对抗检测网络(adversary detector network，ADN)，ADN是一种二分类神经网络，对正常样本和对抗样本的联合训练可以使其对两种样本进行分类。此网络对基于梯度的攻击也有一个较好的检测效果。

2018年，MADRY等[4]提出映射梯度下降(projected gradient descent，PGD)方法，该方法在白盒攻击和黑盒攻击下都能保持较好的鲁棒性，但是其模型本身针对正常样本的表现无法达到最佳效果。TRAMER等[5]提出综合性对抗训练，对其它模型生成的对抗样本也加入到训练集中进行重训练，能够较为有效地解决对抗训练中出现的过拟合问题。SCHOTT等[11]提出综合分析方法，是一种基于生成对抗网络的方法，学习每个分类的非对抗数据输入分布，将对抗样本数据映射到网络学习到的非对抗数据流形中，从而提高模型自身的鲁棒性。

2019年，YANG等[12]提出ME-Net方法，此方法是根据预设的概率阈值随机丢弃图像样本中的像素，并使用矩阵估计法对丢弃的像素进行修复，通过破坏扰动结构来预防对抗样本的攻击。

2 NLM-AT对抗样本防御算法

2.1 非局部均值去噪

非局部均值算法(NL-means)，NL-means是一种滤波算法，图像中每一个像素的像素值由当前像素和周围给定区域中的所有像素值进行加权平均得到，其滤波过程可用式(1)表示

(1)

Ωx是像素x的领域。w(x,y) 表示在图像v中像素x和像素y的相似度，v(y) 表示像素y的领域。在算法运算的过程中，会预设搜索窗口和模板窗口。搜索窗口以目标像素为中心，模板窗口在搜索窗口中进行搜索，计算搜索窗口和模板窗口的相似度。对抗攻击算法按照类别细分可以分为黑盒攻击与白盒攻击、全局攻击与局部攻击、目标定向与目标非定向攻击，这些不同类别的攻击都是在正常样本上添加了微小的扰动噪声。非局部均值算法相比以深度学习为核心的去噪算法，没有训练网络的数据、时间开销，该算法可以在样本全局范围内较好地去除这些噪声并且保留图像的一些细节特征，且该算法是从样本像素数据层面出发进行去噪，不受对抗攻击算法的影响，因此对抗攻击算法无法针对此去噪算法进行攻击。

2.2 去噪与对抗训练关系分析

对抗防御技术相对对抗攻击技术有一定的滞后性，对抗攻击算法形式多样，而且大多对防御算法、模型进行针对性设计，因此不同攻击算法所计算出来的扰动具有多样性，不同扰动之间特征差异较大，像素修改范围、像素修改量都不一样。各个维度上特征的巨大差异使得单一防御算法不能有效防御各类对抗攻击算法的攻击。而防御领域效果较好地对抗训练技术也存在同样的问题，对抗训练是需要依赖数据集的，但是即使使用多种对抗样本数据集进行对抗训练，仍然能找到新的对抗攻击算法对网络进行攻击。

对抗训练技术泛化性不强的很大原因在于未知来源的对抗样本具有多样性，而对抗训练采用的对抗样本相对于大量的攻击算法而言有所局限，并且使用过多的对抗样本数据集会成倍地增加对抗训练难度。如果在进入模型检测前，能尽量保证多种对抗样本扰动特征的统一，并且保证模型进行对抗训练学习到的扰动特征和输入的扰动特征统一，则模型的鲁棒性会有一个较大地增强，能够较好地防御不同的对抗攻击。

引入非局部均值去噪算法有几点优势：

(1)非局部均值去噪算法是在数据层面进行噪点去除，对于现实场景的图像能够在保证去噪效果的同时保留主要的物体实例特征。

(2)非局部均值去噪算法能够对多种分布的噪声进行去除，去除后图像保留的特征有很强的相似性，并且和干净样本去噪后保留的特征也有相似性，保证了不同对抗样本上扰动特征的统一，有利于网络模型的检测、分类。

(3)采用去噪后的对抗样本进行对抗训练，保证了模型学习到的扰动特征和输入样本的扰动特征一致，提高了模型对对抗样本检测、分类的能力。

由上述分析可知NLM-AT算法对于多种攻击算法的防御能力优于单一的对抗训练算法，泛化能力较强。

2.3 算法理论分析

在深度神经网络的目标检测任务中，训练网络需要最小化损失函数以提高网络的检测效果。最小化损失函数可写成如下格式

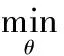
(2)

对抗训练的思想就是将对抗样本加入原有训练集中进行神经网络的训练，提升神经网络对对抗样本的检测能力。因此对抗训练的最小化损失函数可以写成如下格式

(3)

θ为网络模型参数，x为输入样本，y为输入样本标签，D为训练集，Δx为对抗扰动，Ω为扰动空间，L(x,y;θ) 为输入样本的损失函数值。其中Δx有几种常见的计算方式

Δx=N(0，η2)

(4)

(5)

(6)

本文使用4种主流的对抗攻击算法FGSM、I-FGSM、PGD、MI-FGSM进行对抗样本的构建。FGSM算法如下

(7)

I-FGSM算法如下

(8)

MI-FGSM算法如下

(9)

(10)

NLM-AT算法整体对抗训练过程可以写成如下格式

(11)

(12)

x1∈D1,x1∈D2,x1∈D3,x1∈D4

(13)

D=D1∪D2∪D3∪D4

(14)

L1～L4分别为4种对抗攻击算法算出的损失函数值，将对抗训练训练集D按其大小进行四等分为D1～D4。 Δx1～Δx4分别为4种攻击算法构成的对抗扰动。

该算法将对抗训练中对抗样本部分等量替换为去噪后的对抗样本，在训练成本上和传统对抗训练相当，由于去噪后的对抗样本中物体实例特征更加明显，该算法的训练过程还会小幅提升模型对正常样本的学习效果。

2.4 算法描述

本节描述了基于对抗训练和非局部均值去噪的对抗样本防御算法在网络模型训练过程中的主要步骤。首先计算输入样本的梯度并生成对抗样本，然后将对抗样本进行非局部均值去噪并加入到训练集中训练网络模型，直到网络收敛。

训练阶段的具体步骤如下：

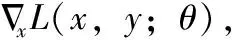
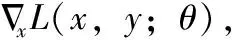
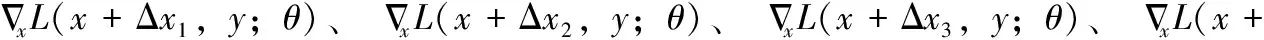
算法模型如图1所示。

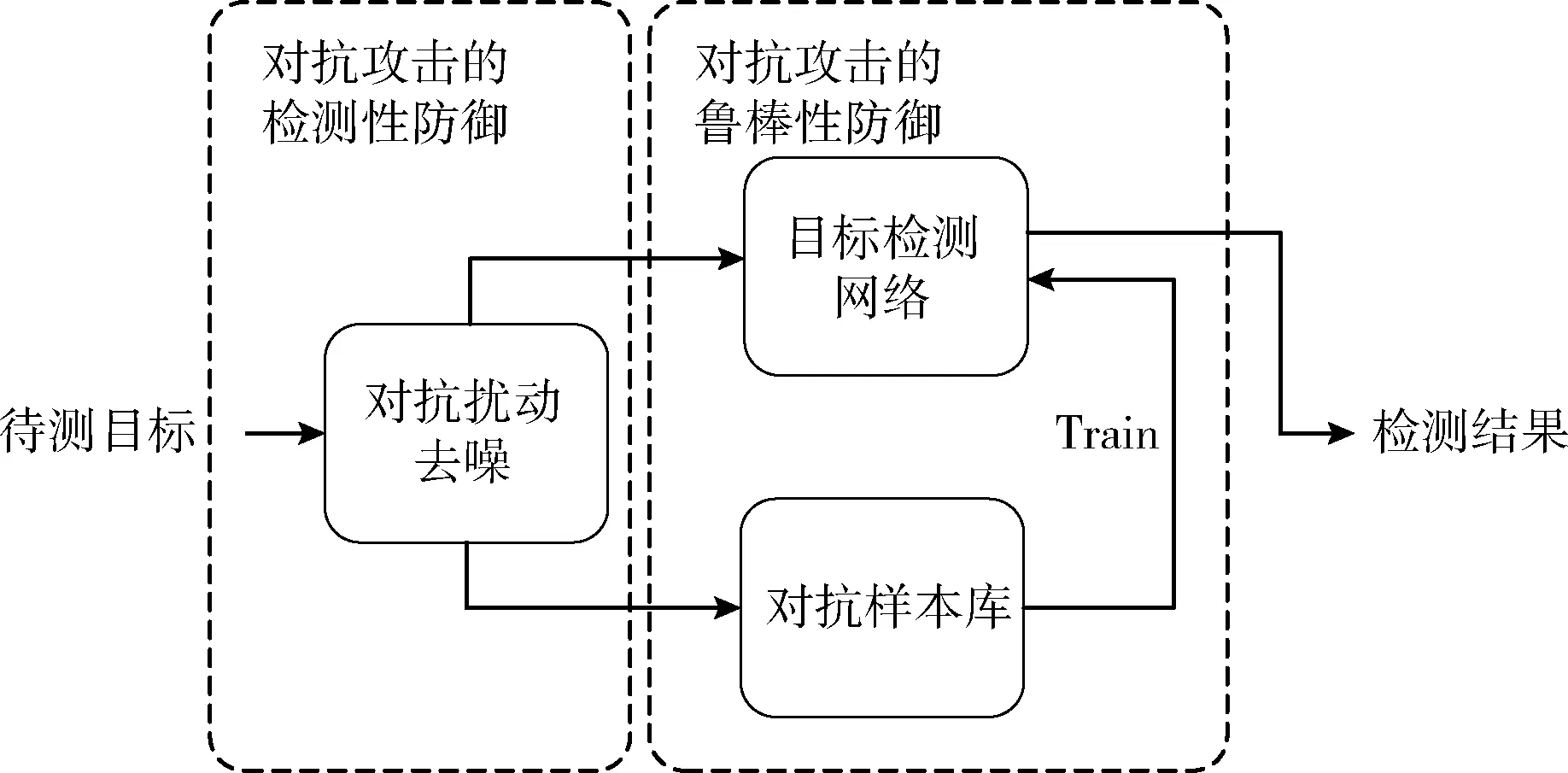
图1 NLM-AT算法模型

本算法从事前、事后两个方面对防御模型进行构建，事前防御为对抗攻击检测性防御，指对抗样本在进入目标检测网络之前进行图像样本去噪，最大可能地去除对抗样本上的扰动，并保留图像样本中物体实例的特征，确保不同对抗样本在进入目标检测网络的时候具有扰动特征的相似性。事后防御指对抗攻击鲁棒性防御，通过更改对抗训练使用的样本，将普通对抗样本更换为去噪后的对抗样本，用其训练目标检测网络，增强模型对去噪样本的检测能力，保证目标检测网络学到的样本特征与输入特征具有相似性。前后配合来保证对对抗样本中物体实例的正确检测，确保检测任务在正常样本、对抗样本的输入下都能正常完成。

在测试阶段，在正常样本的测试集上分别使用FGSM、I-FGSM、MI-FGSM、PGD这4种对抗攻击算法添加对抗扰动，生成5份相同数量、不同类别的测试集，分别测试防御算法在正常样本和4种对抗样本下的检测效果。

NLM-AT伪代码如算法1所示。

算法1：NLM-AT

输入：训练集X，训练集标签Y，网络参数θ，学习率τ，训练轮次N，批次大小M。

输出：训练完毕的网络。

(1)for epoch=1,2,…,Ndo

(2) for batchB⊂XC⊂Ydo

(3) fori=1,2,…,X/Mdo

(4)li←(xi,yi)～B,CL(xi,yi;θ)

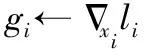
(6)x′i←F(gi)

/*F()为4种对抗攻击算法，x′i为4种对抗样本*/

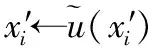
(8)l′i←L(x′i,y;θ)

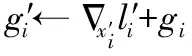
(10)θ←θ-τ·g′i

(11) end for

(12) end for

(13) end for

3 实验结果与分析

3.1 实验设置

对于NLM-AT算法，使用k-means聚类对11 725张样本的目标框进行聚类，提取出9个锚框尺寸9×14，14×28，22×47，23×10，37×18，49×79，68×31，133×163，353×358。设置训练每批次大小为8，训练周期为60。初始学习率为0.001，最终学习率设置为0.000 001，采用学习率预热策略，学习率在刚开始的几个周期先逐渐增大至初始学习率，然后逐渐衰减，直到训练结束学习率衰减到最终学习率。扰动量ε设置为1/255、2/255、4/255，传统对抗训练标记为MADRY算法，对于MADRY、ME-Net算法，采用与NLM-AT相同的参数配置。在conf_loss(置信度损失函数)、giou_loss(广义交并比损失函数)、prob_loss(预测损失函数)、total_loss(总损失函数)4个损失函数上进行收敛学习。使用FGSM、I-FGSM、MI-FGSM、PGD攻击算法进行对比实验。

实验使用的硬件配置为CPU Intel i7-7700K 4.2 GHz，GPU NVIDIA GeForce GTX1080Ti，11 GB显存，32 GB内存；软件配置为Windows10专业版，Pycharm2020.2.3，anaconda4.8.3，Tensorflow2.4.1，python3.7.9。

训练结果使用评价指标均值平均精度mAP(mean average precision)进行评价。

3.2 实验结果

3.2.1 NLM-AT算法防御效果

表1展示了NLM-AT算法在FGSM、I-FGSM、MI-FGSM、PGD种攻击算法，扰动量ε分别采用1/255、2/255、4/255下的防御效果。

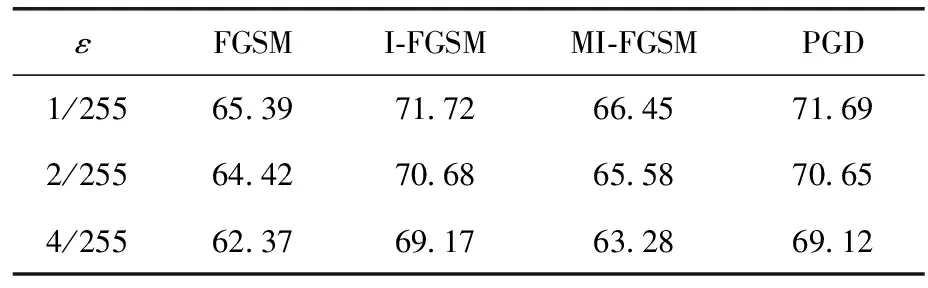
表1 NLM-AT在不同攻击下的mAP/%

由表1可以看出该算法对不同扰动程度、不同攻击算法下均能保持良好的鲁棒性，有较好的防御效果。

图2以可视化的方式展示了该算法的防御效果。左侧一列是目标检测模型对正常样本的检测效果，中间一列是目标检测模型对对抗样本的检测效果，右侧一列是通过NLM-AT算法进行防御的目标检测模型对对抗样本的检测效果。

图2 防御效果

3.2.2 NLM-AT算法与其它算法对比实验

表2展示了NLM-AT算法和传统对抗训练算法在训练集上训练一个周期的时间对比及总时间成本对比，由于两者在对抗样本生成数量的策略上一致，模型学习到的样本总量是一样的，所以NLM-AT算法与传统对抗训练算法时间相当。

表3展示了不同算法对正常样本和对抗样本的防御效果，此处实验的对抗样本为随机抽取测试集中的对抗样本。无防御策略构建的目标检测模型标为normal方法。相比已有方法，NLM-AT算法对正常样本和对抗样本的检测都有一个较好的mAP。

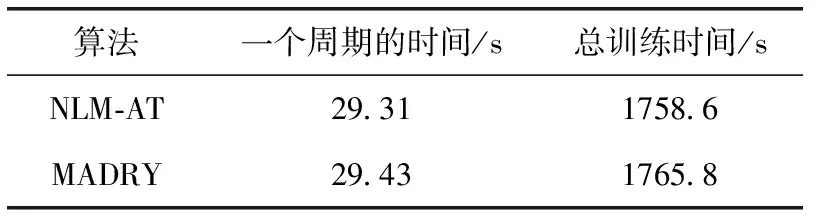
表2 NLM-AT与MADRY时间成本对比

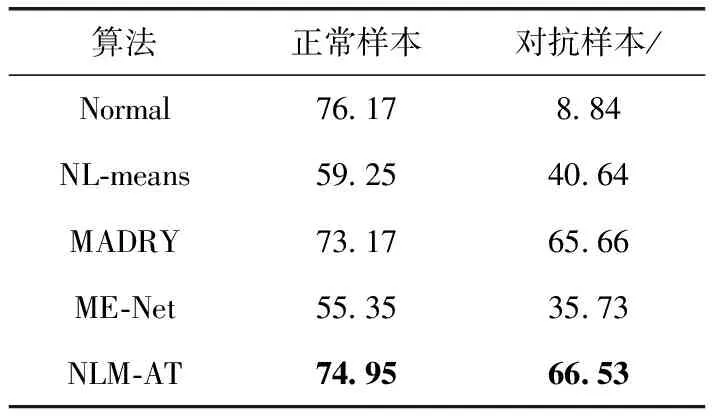
表3 不同算法对两类样本的mAP/%

表4、表5、表6展示了不同算法在FGSM、I-FGSM、MI-FGSM、PGD种攻击算法，扰动量ε分别采用1/255、2/255、4/255下的防御效果。

使用4种攻击算法重新进行超参数设置并对模型进行再次攻击，以考量不同方法在不同攻击下的防御效果。表7展示了不同算法在此攻击条件下的防御效果。

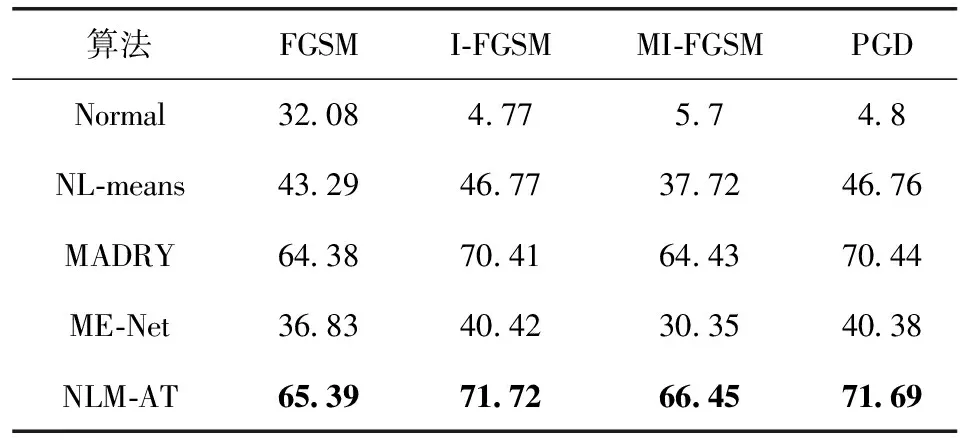
表4 不同算法在不同攻击下的mAP(ε=1/255)/%

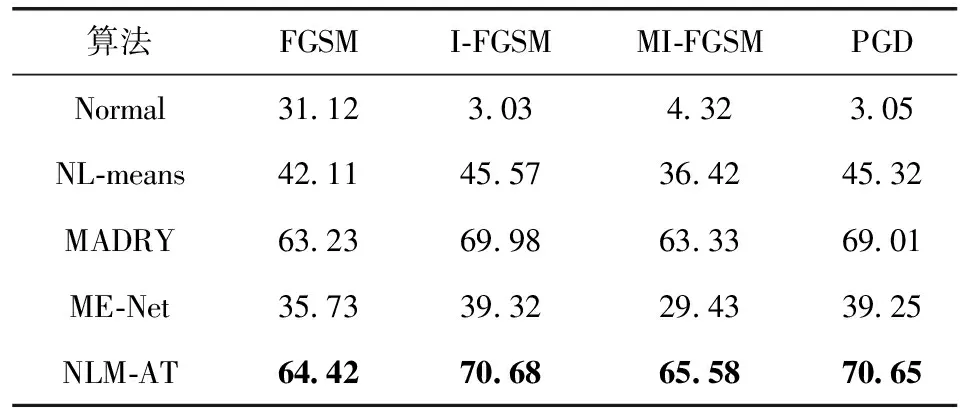
表5 不同算法在不同攻击下的mAP(ε=2/255)/%

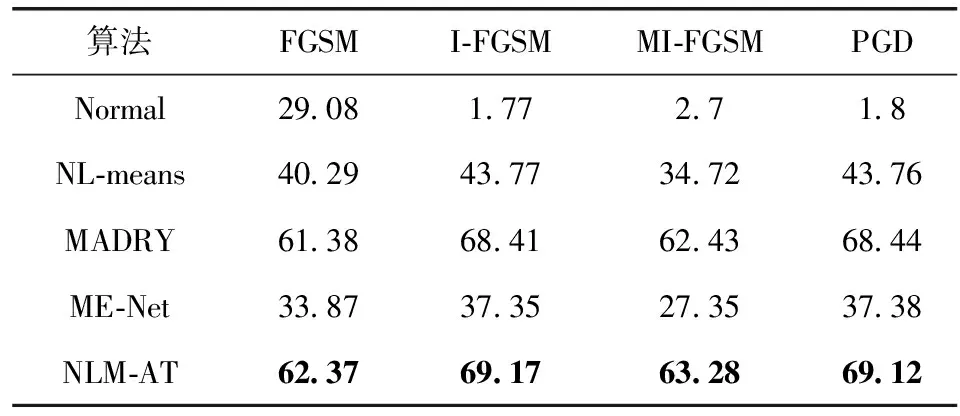
表6 不同算法在不同攻击下的mAP(ε=4/255)/%

表7 不同算法在针对攻击下的mAP(ε=6/255)/%

实验结果表明，NLM-AT方法在不同类型、不同扰动程度的攻击下，对正常样本的mAP保持在74.95%。对于不同的扰动程度，在FGSM攻击下，模型mAP分别提高了33.31%、33.3%、33.29%。在I-FGSM攻击下，分别提高了66.95%、67.65%、67.4%。在MI-FGSM攻击下，分别提高了60.75、61.26%、60.58%。在PGD攻击下，分别提高了66.89%、67.6%、67.32%。与其它方法相比，NLM-AT在不同攻击条件下的mAP均高于其它方法。

由表7可以看出当针对训练完毕的网络模型进行再次攻击时，NLM-AT在不同攻击下的mAP依然高于其它方法，展示了该算法在白盒攻击条件下有着优异的鲁棒性。

为了更加广泛深入地对算法的鲁棒性进行验证。选出4种算法中攻击效果最强的MI-FGSM算法进行实验，通过更改扰动步长α、迭代次数k、扰动量ε进行测试。对抗攻击使用二范数和无穷范数进行测试，实验中的输入样本尺寸均为416×416。

(1)不同步长的攻击对防御算法的影响。图3展示了在迭代次数为10，无穷范数和二范数攻击扰动ε均为4/255时，步长对防御模型mAP的影响。图3(a)、图3(b)分别是无穷范数攻击和二范数攻击下4种防御模型的防御效果。由图中可以看到随着步长增大，各个方法的防御能力都有所下降，但是NLM-AT在此攻击条件下能够保持一个较好的防御效果。

(2)不同迭代次数对防御算法的影响。图4展示了在步长为ε/k， 无穷范数和二范数攻击扰动ε均为4/255时，迭代次数对防御模型mAP的影响。图4(a)、图4(b)分别是无穷范数攻击和二范数攻击下4种防御模型的防御效果。由图中可以看出虽然在迭代次数的增加下，各个方法的防御效果依然有所下降，但NLM-AT与传统对抗训练方法在无穷范数的攻击下基本保持一致的防御效果，并且优于其它两种方法，且在二范数攻击下优于其它3种方法。

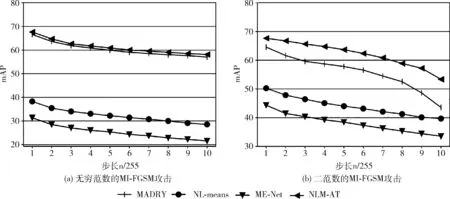
图3 不同步长对防御模型mAP的影响

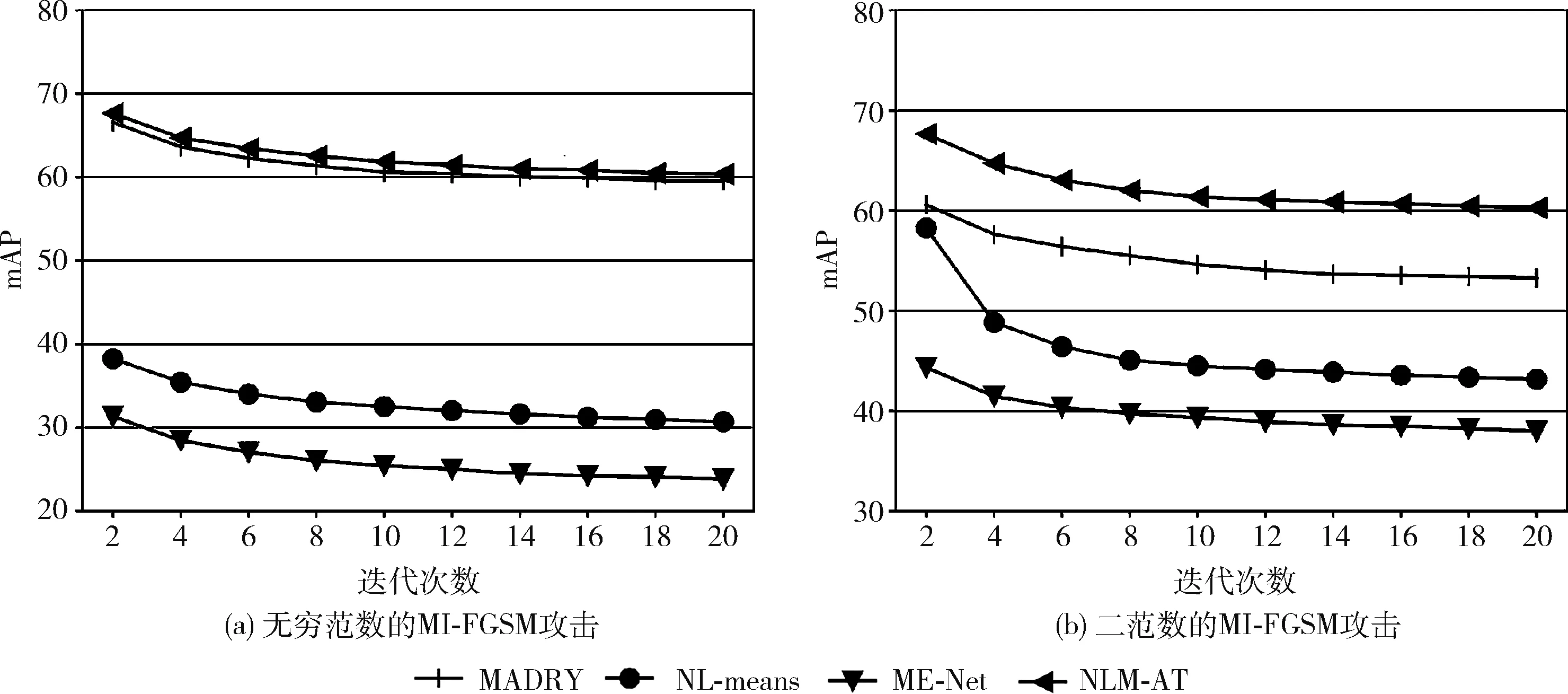
图4 不同迭代次数对防御模型mAP的影响

图5 不同扰动量对防御模型mAP的影响

(3)不同扰动量对防御算法的影响。图5展示了在MI-FGSM攻击条件下，迭代次数为10，步长为ε/k时不同扰动量对防御模型的影响。两种范数攻击的扰动量范围均设置为最小7/255，最大26/255。图5(a)、图5(b)分别是无穷范数攻击和二范数攻击下4种防御模型的防御效果。由图中可以看出无穷范数的MI-FGSM攻击下，NLM-AT与传统对抗训练方法的防御效果基本能够保持一致，并且优于其它两种方法；在二范数的MI-FGSM攻击下优于其它3种方法。

3.3 讨 论

实验基于YOLOv3目标检测模型，在DIOR数据集上使用4种对抗攻击算法FGSM、I-FGSM、MI-FGSM、PGD验证了提出的NLM-AT算法的防御效果。从时间成本上分析了该算法和传统对抗训练算法的区别。对比其它算法，分析了该算法对于正常样本和对抗样本的检测效果，在提高了对抗样本防御效果的情况下，保持了对正常样本的检测效果；分析了在不同扰动程度情况下该算法的防御效果，相同条件设置下NLM-AT均优与其它算法；分析了在模型训练完毕后进行再次攻击的情况下算法的鲁棒性，通过对几种算法训练的模型进行再次攻击，考量了NLM-AT的鲁棒性。总的来说，针对目标检测模型，NLM-AT有效增强了模型对对抗样本的防御能力。

4 结束语

针对目标检测模型易遭受对抗样本攻击的问题，本文结合了检测性防御和鲁棒性防御思想，提出了NLM-AT算法。通过在DIOR数据集上开展广泛的实验，验证了该算法对FGSM、I-FGSM、MI-FGSM、PGD这4类攻击均有优异的防御效果。即使针对训练后的模型进行再次攻击，该算法依然能够保持良好的防御能力，表明该算法对新类型的对抗样本也有较强的鲁棒性。综合来说，NLM-AT算法有效地提高了目标检测模型对对抗样本的检测能力。下一步将优化算法结构来进一步提高算法的防御能力。