带权重的改进天牛须算法解方程组及工程应用

吕昱呈，莫愿斌,2+

(1.广西民族大学 人工智能学院，广西 南宁 530006；2.广西民族大学 广西混杂计算与集成电路设计分析重点实验室，广西 南宁 530006)

0 引 言

方程组的求解一直是难点问题，求解方程组有牛顿法、欧拉法以及锥模型信赖域算法[1]等。传统数值算法求解对初始值设定要求较高，使算法存在局限性。目前优化算法被用在方程组求解中，将方程组转化为目标寻优问题，提供一种解决方案。曾等[2]提出蝴蝶算法融合改进的反向学习和二次插值；黎等[3]提出布谷鸟算法结合差分进化和二次插值求方程组较多解问题。优化算法求解方程组仍有很多问题值得研究，Zhang等[4]所提出改进的布谷鸟算法对非线性方程组的求解只注重单值解值；Ariyaratne等[5]对方程组求解值的精度较低。

为此，提出一种求解方程组的方法，将黄金分割法调整搜索区间的优势融入天牛须算法(BAS)[6]中；添加位置权重改变天牛位置，加强全局寻优能力；加入步长自适应以精确提高天牛后期小范围内搜索的准确性。通过标准测试函数对改进的天牛须算法进行性能测试，将其用于求解方程组和实际工程应用问题，所得结果与其它算法对比表明该算法在方程组解的数量和质量都具有优势，进一步验证了改进算法的寻优能力与求解方程组性能。

1 方程组的优化模型转换

线性方程组，是方程关于未知量均为一次的方程组。非线性方程，是因变量与自变量之间不是线性关系。求解此类方程往往很难得到精确解，需要求近似解问题。相应的求近似解的方法也逐渐得到重视。方程组[2]如下

(1)

(2)

方程组的解对应F(x1,x2,…,xn) 最小值为0的解，所以方程组求解问题可转为求下式的最优解

(3)

因此选择寻优性能好的算法是解方程组问题的关键，对此本文提出基于黄金分割的带位置权重和自适应天牛须算法来验证在求解方程组问题的有效性。

2 天牛须优化算法

天牛须算法是根据天牛觅食为仿生原理的智能优化算法。BAS算法当前在图像处理[7]、路径规划[8]、电力调度[9]等问题得到初步应用。天牛觅食的过程就是天牛须算法的寻优过程。其步骤如下

(4)

stept+1=eta*stept

(5)

(6)

(7)

式(4)是天牛方向向量，n为空间维度。式(5)是天牛步长更新公式，递减因子eta在[0,1]之间，本文取0.95；式(6)中，xl、xr分别表示天牛左右两须位置，xt表示在第t次迭代时天牛质心坐标，d0为左右两须之间的距离长度。式(7)是天牛位置的更新，其中，stept表示第t次迭代的步长因子，sign(·) 表示符号函数。

天牛须算法依靠两条须能够实现快速寻优，但同时也会因为位置更新的方向单一，导致天牛陷入局部最优，由于天牛没有跳出局部最优的能力，降低BAS算法的搜索精度[10]；混合教与学算法的天牛须搜索[11]在一定程度上提高了搜索精度，但仍未求解到最优值，且迭代次数很大也未寻到最优解。基于此提出本文的改进方法，当天牛在搜索过程中陷入局部某个极值时能够跳出限制，同时改变天牛的位置方向使算法在快速迭代收敛的同时有更优的寻优效果。

3 改进的天牛须算法

传统BAS算法有较快寻优能力，由于其初始位置随机性，且在每一步移动过程中方向是随机单一，导致算法在寻优过程中极易陷入局部最优。为解决此问题，本文引入基于黄金分割的带位置权重和自适应的算法，对传统BAS算法进行改进。

3.1 引入黄金分割法

黄金分割法是建立在区间消去法原理基础上的试探方法，每次可以将区间按照一定比率压缩，修正原来的求解范围。即在搜索区间 [a,b] 内插入两点x1，x2， 并计算其函数值，此时区间被分成3段。通过函数值大小的比较，删去其中一段，使搜索区间得以缩短。其原理如图1所示。

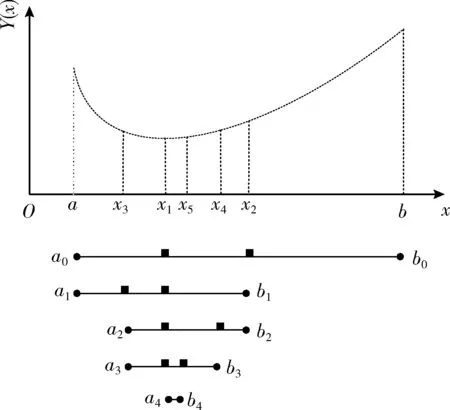
图1 黄金分割算法原理

文中的GRBAS算法是在天牛走完当前这一步时，获取其左右两须的位置值，作为黄金分割法的搜索区间，构成与目标函数值相近的低次多项式，利用黄金分割算子式在搜索区间搜索极值点的方法，每次迭代取试探点

(8)

式中：αk+1和βk+1表示在搜索区间内通过黄金分割法选取的试探点位置。在求解方程组过程中引入黄金分割，把多项式的最优解与原函数的最优解之间的距离逐步减小，是一个收敛速度极快的搜索方法。提升了天牛须搜索算法的局部搜索能力，提高天牛跳出局部最优的能力以及搜索精度的能力。

3.2 带位置权重的天牛

天牛更新位置时，因蓄力等因素做微弱方向位置调整飞到下一个目的地。本文引入“位置权重”因子w，改变天牛位置，增强天牛全局寻优能力，引入位置权重的天牛位置更新方程如式(9)所示

(9)

由式(9)可知，较大的w能加强BAS全局搜索能力，反之，较小的w能加强局部搜索能力。BAS算法本身存在易陷入局部最优的缺陷，要提升全局搜索能力，因此选择较大的w，实验结果表明，w在[0.95,0.96]之间BAS有更快的收敛速度，算法求解精度也得到很大的提高，提高了BAS算法的性能。

3.3 天牛步长自适应

根据式(7)可知，步长step越大，天牛全局搜索能力越强，反之，局部搜索能力越强。本文提出步长自适应机制，算法前期，让天牛在求解空间扩大搜索范围快速寻优，采用大步长因子，算法后期，采用小步长因子。基于上述描述，通过测试验算，本文采用如下天牛步长自适应机制

(10)

式中：stept是第t次迭代时的步长，stepmax表示初始步长长度。原始步长和自适应步长递减情况对比如图2所示。

图2 步长变化对比

传统BAS算法每次的步长变化均匀，天牛极易探索到某个范围陷入局部最优，导致求解错误；引入步长自适应机制后，GRBAS算法的步长在开始搜索时可以进行大范围空间搜索；迭代到中间次数时，步长缩短变快，促使搜索范围的收缩；迭代后期，步长缩短减弱，使算法查找寻优更精确，丰富全局搜索能力，提升搜索精度。

3.4 算法流程

基于黄金分割的带位置权重和自适应的天牛须算法的流程如图3所示。

图3 算法流程

改进天牛须算法(GRBAS)伪代码如下所示：

Algorithm GRBAS.

Input： set direction vectordir; distance between the two beetles’ antennaesd; step lengthstep; max iterationn; spatial dimensionk；

Output：Best valuefbest.

(1)Set the initial position of beetlex=rands(k,1);

(3)fori=1 ton

(4)Initilization beetle direction vectordir=rands(k,1);

(5)Calculate the position of two beetles’antennaes;

(6) Initilization beetle antennae coordinatexleft、xright;

(7) Calculate the fitness of thexleftandxright；

(8)Change range through golden ratio:x0=xright*w+0.382*(xleft-xright)andx1=xright*w+0.618*(xleft-xright);

(9) Calculate the fitness of thex0 andx1;

(10)Update the range of two antennaes of beetle;

(11)end

(12)Adaptive step size;

(13)Update the position of beetle through w:x=x*w-step*dor*sign(fleft-fright);

(14)fbest_store=the fitness of the best value;

(15)returnfbest_store;

4 测试与结果分析

为测试GRBAS算法的寻优能力和精确度，对10个标准测试函数进行测试。最后，将GRBAS算法运用在求方程组的解。包括3个线性方程组和3个非线性方程组。

4.1 标准测试函数的测试

表1是标准测试函数相关参数设置，表2给出7种算法的实验结果。算法最大迭代次数均为900，粒子群算法(PSO)、人工鱼群算法(AFSA)和改进的海鸥算法(MSOA)种群数目为200，学习因子为2，惯性因子0.8，人工鱼最大步长0.1，感知距离为1。MSOA螺旋系数u和v初始为0.1。BAS和GRBAS算法初始步长设为1。蚁狮算法(ALO)和乌燕鸥算法(STOA)的寻找群体数目为40。每个函数均运行20次，分别统计7种算法的平均值，最优值以及最差值。图4～图13为每个函数迭代曲线。

表1 标准测试函数的相关参数

表2 7种算法实验结果

表2(续)

表2(续)

图4 函数f1的迭代曲线

图5 函数f2的迭代曲线

图6 函数f3的迭代曲线

图7 函数f4的迭代曲线

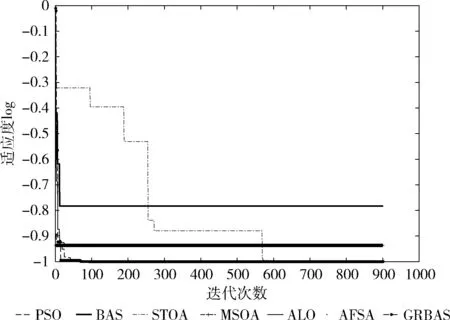
图8 函数f5的迭代曲线

图9 函数f6的迭代曲线

图10 函数f7的迭代曲线

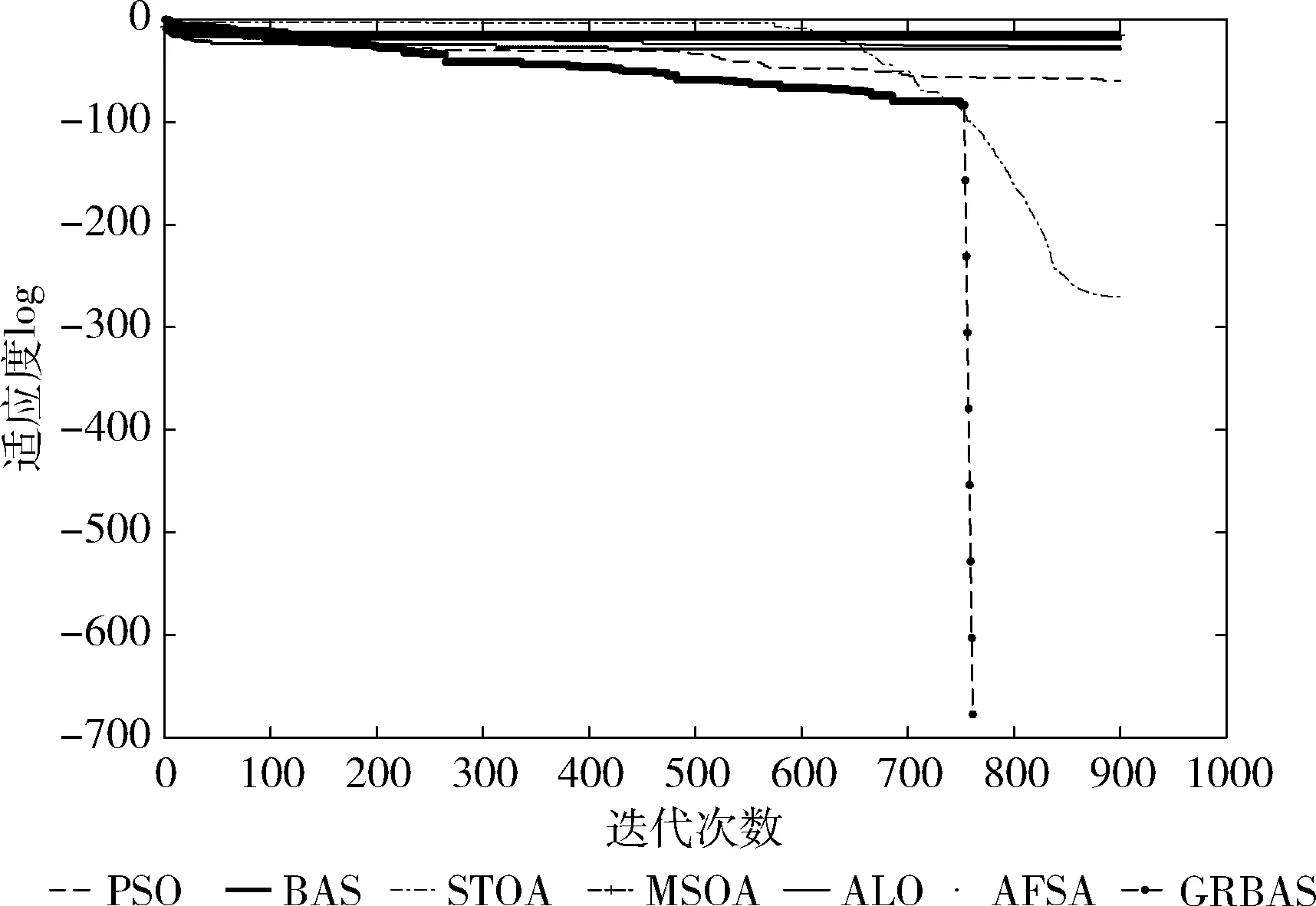
图11 函数f8的迭代曲线

图12 函数f9的迭代曲线

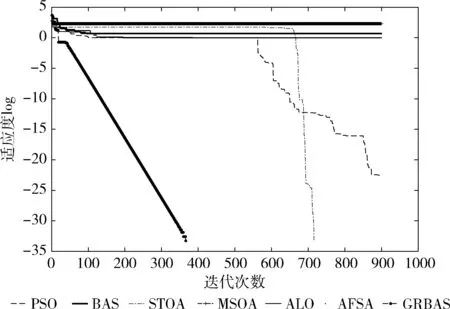
图13 函数f10的迭代曲线

4.2 结果分析

通过7种算法对比，GRBAS算法对测试函数f1、f2、f3、f4、f5、f7、f8、f9、f10的计算都收敛到最优值，比其它算法在求解精度和准确率都高。对于函数f6，GRBAS有求解到最优解的情况，MSOA、STOA算法求解陷入局部最优，原始BAS算法的解值范围极不稳定，而GRBAS算法的解值稳定。

对比图4～图13可知，函数f1、f3、f4、f8，GRBAS算法在迭代次数约720次就求得最优解停止迭代，其它算法在设定的900次迭代后仍未收敛到最优；函数、f5、f7、f10，GRBAS算法在迭代初期就能寻优求到最优值，其它函数均有不同程度的陷入局部最优或在最大收敛次数后仍未求解出最优解的情况；函数f2、f9算法GRBAS在迭代约250次求得最优解，而其它算法在900次迭代后仍未停止求解；函数f6，GRBAS算法的收敛效果较其它算法更平稳。

由此知改进的天牛须算法计算精度和稳定性都有较明显提升。验证基于带权重的改进天牛须算法寻优的有效性，表明GRBAS算法能够在算法陷入局部最优时有效跳出局部搜索范围，同时在高维空间下，搜索解的能力较好，解值更接近与理论值。

4.3 方程组的求解

为了测试该算法求解方程组的性能，选取3组线性方程组[12]和3组非线性方程组进行测试，每个方程均独立运行10次，将结果取平均值，实验结果如表3所示。线性方程组如下

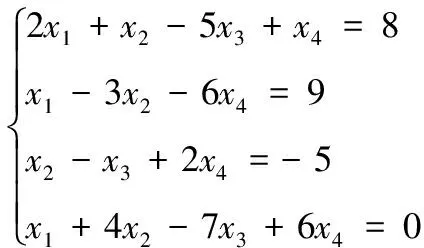
理论值： (1,2.5,3,6.5,7)

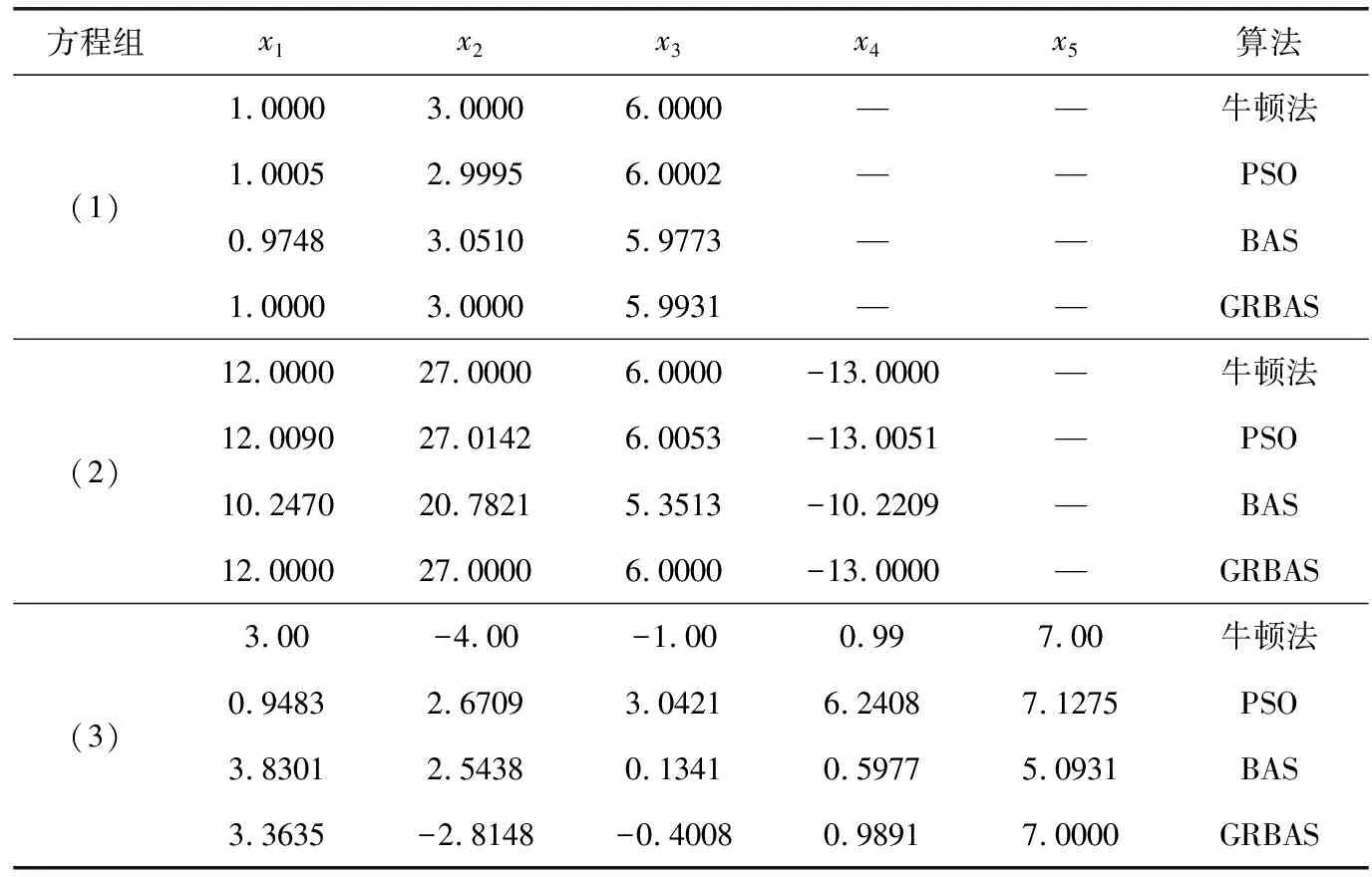
表3 线性方程组的实验结果

文中引入文献[3]中的非线性方程组进行仿真实验，非线性方程组如下

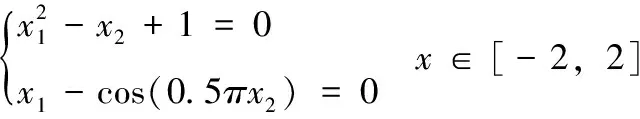
理论值： (-0.707 106 78,1.5)(0,1)(-1,2)

理论值：(1.546 342,1.391 174)(1.067 412,0.139 460)

近似理论值：x1=-0.451 123，x2=0.445 178

对3个非线性方程组仿真测试结果见表4。

结果分析：从表3知，经典牛顿方法能够求出理想值，方程组(1)和方程组(2)，PSO、BAS以及GRBAS算法求出的值都接近理想值，GRBAS的求解精度更好；方程组(3)PSO算法的求解值偏离理想值，BAS和GRBAS算法的求解值较理想值接近，但是GRBAS的求解精度更好。

从表4知，对于方程组①，文献[13]和HCS能够找出方程组的全部解且其值接近于理论值，BAS算法虽能求得全部解但求解精度不高，而GRBAS算法更具有优势，求解精度上更好；方程组②，牛顿法只能求出一个解，PSO算法和BAS算法的求解与理想值有一定的差距，HCS算法和GRBAS算法的求解精度相近，但GRBAS算法精度更高；方程组③虽然没有求解到近似解值，但是比BAS、PSO算法求解结果更好，其解值与HCS结果相近，但是在求解精度上GRBAS算法更精确。通过实验结果分析，GRBAS算法具有较好的求解能力。

5 工程应用

工程中许多问题要用方程组求解，如三电平逆变器问题[14]，为逆变器SHEPWM的非线性方程组求解对调制技术提供新方案，使开关角度更易于收敛；供电网络系统各节点电压的求解；悬索桥鞍处主缆长度的计算要对二元非线性方程组进行求解。

5.1 工程领域中方程组

在建筑工程的相关实际操作中，如钢筋混凝土结构的研究问题通常会归结到三角函数超越方程求解结果的实零点。求解三角函数超越方程组常用牛顿迭代法和梯度下降法，使用这两种算法在初值选取时有较高的要求。求解三角函数超越方程其极值的位置是很困难的。该类超越方程经过恒等变形、代换和消元，可归结为含有一个变量的方程组

F(x)=(F1(x),F(x),…,F(x))T=0

(11)

表4 非线性方程组①-③的实验结果

其中，x=(x1,x2,…,xn)T为n个变量。由于三角函数在区间上是一个周期函数，在区间内方程组的实零点不唯一，针对这一特点，使用改进天牛须算法进行求其全部实零点。为了测试GRBAS算法在求三角函数超越方程组的性能，文中引入了文献[15]中的超越方程组作为算例1进行仿真实验

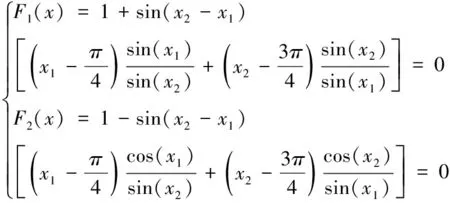
(12)

通过仿真测试，求得方程组(12)全部实数解表5所示以及误差值对比见表6。

表5 GRBAS算法求解结果

表6 误差分析

本文引用文献[16]中的超越方程作为算例2。其超越方程式(13)如下

(x-1)2sin2x+(x-1)3cos3x+5(x2-1)=0

(13)

求解该超越方程在区间[-5,5]内的根。通过GRBAS算法仿真运行，运行结果保留6位小数点，其结果与文献结果对照见表7。

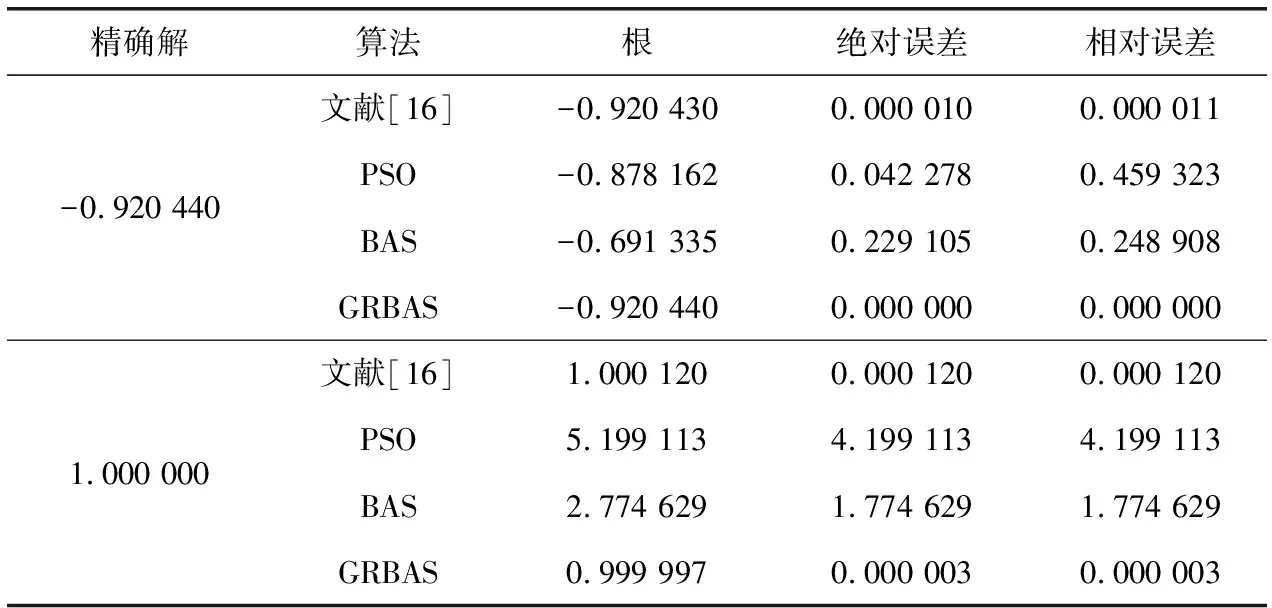
表7 GRBAS算法与文献结果对比

5.2 结果分析

用GRBAS算法对三角函数超越方程的仿真实验与算例1中文献[15]的数据对比知，PSO算法没有很好的求解到最优值，每组解的误差很大；文献[15]使用牛顿法，其收敛性依赖于初值选取，造成求解结果数量受局限；本文算法比牛顿法求解的精度更高，同时算出3组文献[15]中未求解出的解组。对3种算法的18组解进行误差比较知，GRBAS算法的误差均匀。平均误差比牛顿法求解略高一点，是由于在所给出的解集中有个别解组解值的精度较低影响整体平均误差值。在其它解组GRBAS算法在解值的精度上更好。算例2中GRBAS算法的仿真结果与文献[16]中结果对比知，GRBAS算法能很好搜索求解到精确值。文献[16]的方法最大相对误差为0.000 120，GRBAS算法最大相对误差为0.000 003。表明改进天牛须算法有效解决了在建筑工程领域里，钢筋混凝土相关问题中常见的非线性方程组多解问题。工程应用实例求解超越方程证明GRBAS算法在求解方程组的有效性和正确性。

6 结束语

本文针对基本天牛须算法存在易陷入局部最优、求解精度低的不足，提出一种带位置权重的黄金分割自适应天牛须算法(GRBAS)。将黄金分割法引入天牛须算法中，把天牛左右两须的位置作为黄金分割的区间边界；引入“位置权重”影响当前天牛位置，利于改变天牛受局部范围的困扰，再对天牛采用自适应改变每一次迭代的步长，使算法在前期搜索范围更广，后期收敛更精确。通过标准函数测试、线性和非线性方程组的求解，以及用于求解工程实际中三角函数超越方程组，均获得满意效果。表明了GRBAS算法的有效性和可行性，其在跳出局部最优能力、求解精度方面均优于基本的BAS算法。