基于改进蚱蜢优化算法的特征选择机制
李雯婷,韩 迪,叶符明
(1.贵州商学院 计算机与信息工程学院,贵州 贵阳 550014;2.广东金融学院 信用管理学院,广东 广州 510521)
0 引 言
特征选择是数据处理、数据挖掘的预先步骤,主要目标是选择相关性和信息化程度高的特征子集,消除非相关冗余特征,提高分类器学习效率[1]。目前,特征选择主要有过滤法和封装法[2]。过滤法主要利用数据关联的统计手段决定特征关联,方法与学习模型无关。例如信息增益、互信息、主成分分析等。此方法的冗余特征过多、选择精度差。封装法将机器学习的思想关联至特征子集的选择过程中,能够降低特征子集的维度。而特征选择的目标是同步实现数据集分类的准确率最高和特征选择量最小,该问题可视为优化问题。
近年来,群智能算法广泛应用于特征选择问题。如GWO算法[3]、ALO算法[4]、WOA算法[5]、BA算法[6]、SSA算法[7]均在特征选择领域得到应用,并取得了不错的性能表现。蚱蜢(也称蝗虫)优化算法GOA[8]是近年来提出的一种新型群智能算法,它模拟了蚱蜢在不同成长阶段的行为特征,具有较强的全局搜索能力,已广泛应用在调度优化[9]、机器人寻径[10]、医学细胞供应预测[11]等诸多领域。
然而,标准GOA依然存在寻优精度差、收敛速度慢的不足。为此,文献[12]引入正余弦机制协调算法全局搜索和局部开发,利用变异使算法能够跳离局部最优。文献[13]提出结合模拟退火和曲线自适应的蝗虫优化算法,对算法全局寻优能力和局部最优跳离进行了优化。文献[14]提出融合变异和均匀分布的蝗虫优化算法,以分段思想作位置更新,使算法更好寻优。文献[15]设计对立学习蝗虫优化算法,文献[16]利用混沌系统均衡全局搜索和局部开发,都实现了标准GOA算法的性能提升。
鉴于已有工作针对GOA算法在开发与搜索间的均衡、提升收敛速度及跳离局部最优问题上的改进仍有片面性,本文具体工作为:设计一种融合完全随机性的混沌Tent映射实现种群初始化,丰富种群多样性和遍历性;利用学习自动机对调整系数c更新,均衡全局搜索与局部开发;引入折射对立学习位置更新机制,避免陷入早熟收敛。将改进GOA算法应用于特征选择问题,设计新的特征选择算法LRGOAFS,实验证明LRGOAFS可以同步降低特征选择维度和提升数据分类准确率。
1 蚱蜢优化算法GOA
蚱蜢优化算法GOA是一种较新的自然启发式算法,模拟了蚱蜢这类昆虫的社会行为。蚱蜢这类害虫会影响农作物产量,其整个生命周期由3个阶段组成:虫卵、幼虫和成虫。在幼虫阶段,蚱蜢的运动特征包括跳跃和柱状旋转式飞行,步长小,移动慢,捕食路径上的植被;而成虫阶段,蚱蜢则以群体方式大范围迁移,步长大,且具有突然性。GOA算法则通过幼虫阶段的局部开发和成虫阶段的全局搜索,促使种群向目标移动,实现目标搜索。蚱蜢个体位置的数学模型为
Xi=Si+Gi+Ai
(1)
式中:Xi为蚱蜢i的位置,Gi为蚱蜢i的重力,Ai为蚱蜢所受风力,Si为蚱蜢i与其它种群个体间的社群作用力,定义为
(2)
式中:dij=|xj-xi| 为蚱蜢i与j间的距离,d′ij=(xj-xi)/dij为个体i至个体j间的距离单元矢量。函数s可视为社群作用力的强度,定义为
s(r)=fe(-r/l)-e-r
(3)
式中:f为吸引力强度,l为吸引力步长。搜索食物过程中,蚱蜢会根据社群作用力建立3类区域:舒适区、吸引区和排斥区。当蚱蜢间的距离逐步增大时(大于10),函数s趋近于无法产生社群作用力,即个体间没有相互影响的作用力。一般做法是将个体位置限制于区间[1,4]。而处于舒适区个体的位置不进行更新。
Gi定义为
Gi=-ge′g
(4)
其中,g为引力常量,e′g为指向地心的单元矢量。Ai定义为
Ai=ue′w
(5)
其中,u为漂移常量,e′w为风向单元矢量。将相关参数代入式(1),有
(6)
其中,N为种群中的蚱蜢数。
通常情况下,个体受到重力G和风力A的作用较弱,种群个体仅依据社群作用力S的影响进行位置更新。因此,可将位置更新方式定义为
(7)

(8)
其中,cmax为调整系数的最大值,cmin为最小值,l为当前迭代数,L为最大迭代数。
GOA算法伪代码如算法1所示。
算法1:标准GOA算法
(1)initialize the value of the parameters such as population sizeN,cmax,cmin,L
(2)generate a random populationX
(3)set the current iterationl=1
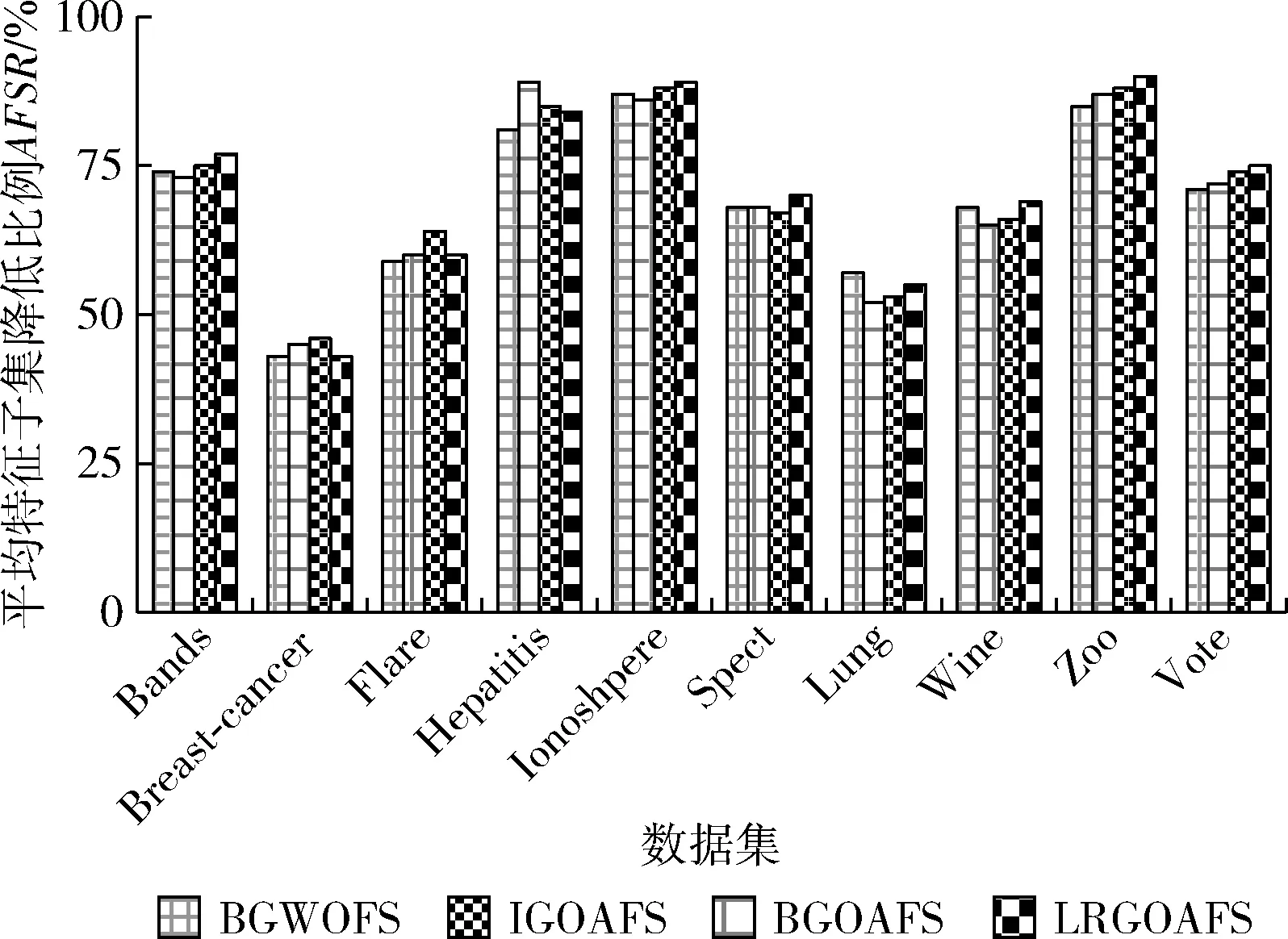
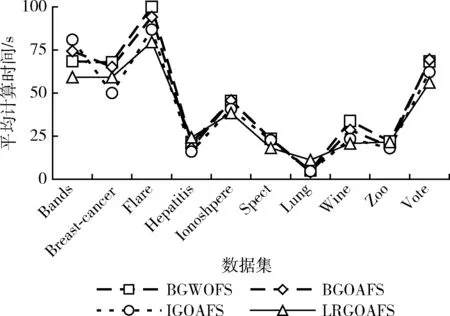
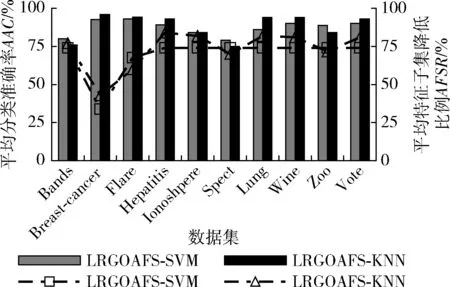
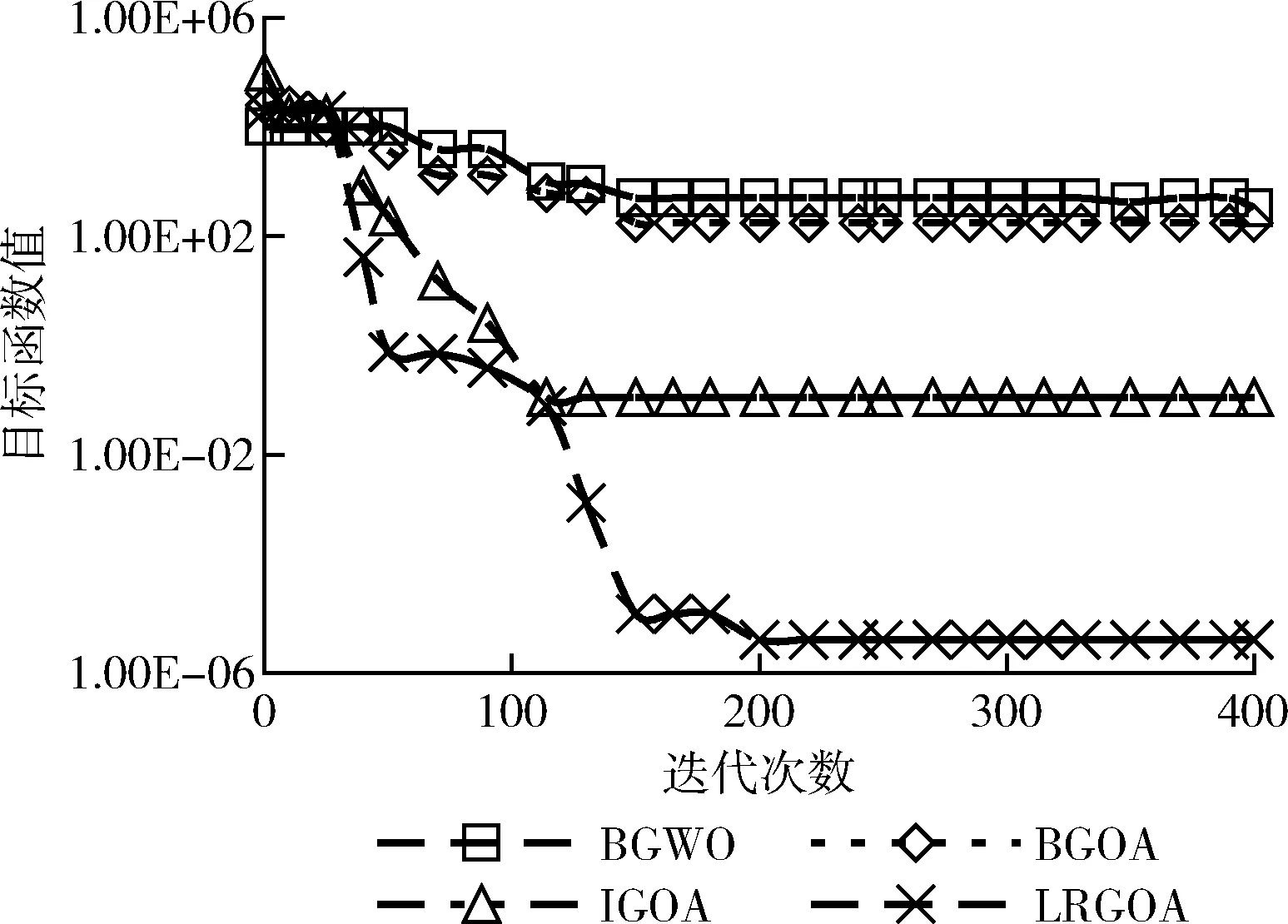
(4)whilel (5) compute the fitness functionf (7) update the value ofc (8) fori=1 toNdo (9) normalize the distance between the solutions inXin the interval [1,4] (10) updatexi∈X (11) end for (12)l=l+1 (13)end while 初始种群的分布对群智能算法的寻优速度和精度有着关键影响。GOA算法通过随机方式进行个体的初始化操作,这会导致种群多样性缺乏,无法个体对空间的遍历性。改进算法借助于混沌系统的随机性、遍历性特征,提升种群多样性。目前,较为常用的混沌映射系统是Logistic和Tent混沌系统,如图1所示(100次迭代生成的混沌值)。可见,Logistic映射比Tent映射遍历性更差,在[0,0.1]、[0.9,1]两个区间取值率较高(边缘位置密度高),中间密度较低,且对初始参数较为敏感。Tent映射均匀性好于Logistic映射,但Tent映射存在小周期、周期点不确定的不足。综合考虑,改进算法在Tent映射中融入完全随机化,添加随机变量r/N改变混沌Tent原来的映射方式,具体方式为 (9) 式中:i为种群规模,j为混沌序号,对应个体空间维度,θ为随机数,μ为混沌参数,且θ∈[0,1],μ∈[0,2]。 确定混沌参数μ并对式(9)取相应初始值后,通过式(10)进行位置映射 xi,j=oi,min+yi,j×(hi,max-oi,min) (10) 式中: [oi,min,hi,max] 为位置xi,j的上下限。 图1 混沌映射 随机生成种群无法保证初始个体均匀遍布完整搜索域,进而降低搜索精度。而根据式(9),混沌序列的生成值取决于初始值,而初始值所发生的微小变化也会导致混沌序列值发生巨大变化,此时生成的初始种群将兼具随机多样和遍历性等特征,这样可以通过迭代均匀地遍历到整个搜索区域。 根据式(7)可知,蚱蜢位置更新时需要两次利用调整系数c1和c2,其中,c1类似粒子群优化PSO的惯性权重,c1的作用是控制全局搜索与局部开发间的均衡。c2的作用则是减少个体间的吸引域、舒适域和排斥域,逐步减小吸引力和排斥力。然而,根据式(8)可知,调整系数是线性递减的,导致全局搜索与局部开发切换、不同域内的个体所受吸引力和排斥力都以相同概率进行,这并不能满足最优的蚱蜢寻优过程,搜索精度会受到影响。因此,两个调整系数的更新必须以非线性形式进行更新。本文将引入以下的学习自动机对调整系数进行动态更新。 随机环境中,可执行的行动数通常是有限的。当执行输入行动集中的一个特定行动时,环境将给出一种反馈(奖励或惩罚)。学习自动机的关键目标是通过分析过往行动及相应反馈选择最优行动,即:通过调整每个行动被选中的概率分布,并使概率值最终收敛到最佳行动上。学习自动化中,初始所有行动拥有相同概率,随机选择一种行动并观察环境反馈。基于反馈结果,更新行动概率。通过若干次迭代学习,LA将选择获得环境奖励的最优行动集。一个可变结构的学习自动机可定义为六元组 (B,Φ,Ψ,P,G,T), 其中,B为输入行动集,Φ为内在状态集,Ψ为环境反馈集,P为每个行动被选择的概率矢量,G为概率更新策略,T为学习算法。 本文利用线性奖惩策略作为学习算法,两个学习参数a、b用于更新学习自动机的行动选择概率,其中,a为奖励步长,b为惩罚步长。本文假设两个学习参数a、b相等,以确保每次迭代拥有相同的概率更新。令αi为时刻t的行动选择,p(t)为行动选择概率分布函数,β为相应环境反馈。对于β∈{0,1} 的特定环境反馈,拥有r个行动(B中行动数)线性奖惩策略可定义为式(11),即β=0的奖励反馈;和式(12),即β=1的惩罚反馈。 当β=0时 (11) 当β=1时 (12) 其中,i为前一步骤中自动机的状态,j为自动机更新后的状态。i=j表明保持前一行动选择,i≠j表明需要改变行动选择。 结合以上分析,本文将利用学习自动机对调整系数c1和c2进行非线性自适应更新,具体定义为 c1=c1+k1δ (13) c2=c2+k2δ (14) 其中,δ为较小正常量,k1、k2为决策参数,即行动集 {-1,0,1}。 初始时,3种行动取值概率相等。随着迭代的进行,行动选择概率将根据线性奖惩策略进行更新,即通过式(9)、式(10)的奖惩策略更新k1、k2在行动上的选择概率。根据将选择环境反馈β进行更新,β=0代表自动机将获得奖励,β=1代表自动机将获得惩罚。通过比较个体适应度优劣,确定环境反馈是奖励或惩罚。若新个体的适应度优于原始个体,则自动机获得奖励,β=0;否则,β=1。通过这种更新方式,算法所选择的调整系数更新将是使得个体能从环境中获得奖励的最优行动选择带来的结果。 对立学习是一种丰富候选种群个体质量的有效方式,它综合利用了当前解的对立解的方式对候选种群的分布范围进行了扩展,即同时在当前解和对立解的方向进行搜索,提高寻得较优解的可能性。 定义个体i的位置为Xi=(xi,1,xi,2,…,xi,d),xi∈[oi,hi], 代表d维空间中问题的一个候选解, [oi,hi] 为个体i在维度上的搜索范围。Xi的对立解为X′i=(x′i,1,x′i,2,…,x′i,d),x′i,j为原解Xi中xi,j的对立数,i=1,2,…,N,j=1,2,…,d, 且对立数x′i=oi+hi-xi,xi∈[oi,hi]。 在计算个体位置适应度的同时,同步考虑其对立解的适应度,将候选解及其对立解同步考虑在种群中,并通过贪婪选择策略择优保留个体至下一代种群,即为常规的对立学习机制。 然而,对立学习仅能在种群迭代早期提升算法的寻优性能,在迭代晚期,对立解也可能陷入局部最优。而折射对立学习则在对立学习基础上,应用光线的折射原理来扩大搜索范围,增加搜索全局最优解的概率。光的折射定理指出:真空中的光线射入另一介质时,入射光线、折射光线及法线处于同一平面。折射角小于入射角,且随入射角增加而增加,具体原理如图2所示。 图2 光线的折射原理 令原始解为x,折射解为x″,入射角为ρ1,折射角为ρ2,入射光线长度为m,折射光线长度为m′, [o,h] 为蚱蜢维度位置的搜索范围,则 (15) 则光线的折射率φ为 (16) 令z=m/m′, 可得折射对立解为 (17) 若z=φ=1, 则折射对立解退化为对立解。 图3是当前解、对立解及折射对立解的位置可能分布情况。可见,若按对立解x′方向搜索,候选解将逐步远离最优解,即使个体适应度得到改善,也可能是局部最优。然而,折射对立解的分布区域明显与最优解距离更近,更利于算法得到全局最解。为了使折射对立解逐步靠近最优解的邻近区域,可以调整入射解改变参数z、φ的取值使更靠近最优解的折射对立解x″2或x″3进一步接近最优解区域,如:减小入射角ρ1降低折射率φ使折射对立解x″2接近最优,或增加折射光线长度m′减小z值使折射对立解x″3接近最优。 图3 当前解、对立解及折射对立解的分布 引入折射对立学习机制进行个体位置更新后,通过折射率φ或入射/折射光线长度比z的调整,有能力使LRGOA算法扩展搜索区域,提高种群多样性,避免过早陷入局部最优。 LRGOA算法步骤如下: 步骤1 对种群规模N,最大迭代数L,混沌参数μ,调整系数最大值cmax和最小值cmin、常量δ等参数进行初始化操作; 步骤2 利用修正的混沌Tent映射方法形成初始化种群; 步骤3 计算种群个体适应度,确定最优解; 步骤4 利用学习自动机机制更新调整系数c; 步骤5 首先利用式(7)更新所有种群个体位置,再根据折射对立学习机制计算个体的折射对立解,通过贪婪选择策略,保留原始解和其折射对立学习解中适应度较优的解至种群中,且种群规模保持不变; 步骤6 重新计算种群个体适应度,更新最优个体; 步骤7 迭代寻优过程结束,转到步骤8;否则,重复步骤4~步骤6; 步骤8 输出最优解。 针对包含若干属性的数据集而言,特征选择是二值决策优化问题,存在的理论解是指数级的。利用LRGOA算法进行特征选择可以通过群智能算法独有的启发式搜索机制极大减小搜索空间和时间复杂度。然而,特征选择解仅为取值0或1,1代表选择该特征,0代表不选择该特征。而LRGOA算法是针对连续优化问题的算法,因此,需要将蚱蜢个体位置改变从连续变化转化为二值变化。 表1代表一种特征选择解,可将其视为蚱蜢个体在搜索空间中的位置矢量。矢量长度代表数据集的特征属性总量,即8个原始属性。矢量元素xi,2=xi,3=xi,5=xi,7=1, 代表2、3、5、7被LRGOA算法选择在最优特征子集,矢量元素xi,1=xi,4=xi,6=xi,8=0, 代表特征1、4、6、8未被选择为最优特征。分类器将根据特征2、3、5、7进行数据分类。 表1 特征选择解 利用Sigmoidal函数(S型)实现LRGOA算法的二值转换,将连续蚱蜢优化算法转换为二进制形式,定义为 (18) 式中:ΔXl表示迭代l时搜索个体的步长矢量,函数T表示特征子集中元素取值为1的概率。 个体位置将基于概率值T(ΔXl) 进行更新,具体为 (19) 其中,rand为随机值。 对于封装法下的特征选择方法,需要结合学习算法评估所选特征子集优劣。本文将采用k最近邻分类器KNN获取相应解的分类准确率。分类准确率越高,表明解的相关性越好。同时,由于特征选择还需要尽可能减少选择特征量,解中特征数量越少,也表明解的性能越优。因此,需要综合考虑这两个冲突式目标设计特征选择算法的适应度函数。本文通过式(20)定义平衡兼顾每个搜索个体的特征选择量(最小化)和分类准确率(最大化)的适应度函数来评估所选特征子集的质量 (20) 式中:ErrRate表示利用所选特征的分类错误率,即分类器错误分类在总体分类中的占比,取值0到1之间,|SF|表示特征选择量,|ALLF|表示原始数据集的属性总量,ξ表示控制参数,用于控制算法对分类质量和特征子集长度的偏好,ξ∈[0,1]。 算法组成结构如下:首先,对数据集进行预处理,将其划分为测试集和训练集;其次,将数据集中的特征分布映射至种群个体位置的搜索空间中,使特征选择问题与个体位置匹配;然后,进入LRGOA算法的寻优过程,该过程主要通过折射对立学习机制对个体位置(对应特征选择解)进行动态更新,其中的调整系数c将以学习自动机进行更新,从而更好提高搜索精度;通过不断更新种群最优解,最后,在到达算法终止条件时,输出最优个体即特征选择最优解。图4是基于LRGOA算法的特征选择过程。 图4 LRGOAFS特征选择算法流程 为了验证基于LRGOAFS算法的特征选择方法的有效性和稳定性,选取UCI库中(https://archive.icu.uci.edu/ml/index.php.)的10个数据集进行实验测试分析,数据集描述见表2。实验环境为操作系统win 10,CPU为i7 2.2 GHz,内存为8 GB。种群规模设置为30,最大迭代次数设置为100,混沌参数μ设为0.7,调整系数最大值cmax为1,最小值cmin为0.000 01、常量δ为0.1,控制参数ξ为0.99(通常分类准确率相对特征选择量具有更大的重要性)。作为群智能算法,LRGOAFS算法下特征选择过程具有一定随机性,在数据集上执行10次独立实验并取均值结果以降低偶然因素对算法计算结果的影响。实验实施中,利用10-折交叉验证(10-folds cross-validation)选择训练样本和测试样本。将每个数据随机划分为10个部分,9个部分作为训练集,剩下1个部分作为测试集。分类器KNN中参数k=5。图5是相应实验过程图解。 表2 数据集说明 图5 实验过程 选择基于灰狼优化的特征选择算法BGWOFS[17]、蚱蜢优化特征选择算法BGOAFS[18]和改进蚱蜢优化特征选择算法IGOAFS[19]进行性能对比。本文基于LRGOA的特征选择算法命名为LRGOAFS。BGWOFS采用了较新的同为群智能算法的灰狼优化算法GWO对特征选择进行求解,BGOAFS则采用标准GOA算法进行了特征选择求解,IGOAFS则在改进标准GOA算法寻优精度和效率的基础上再求解特征选择问题。BGWOFS算法中,收敛因子a的取值范围为[0,2]。BGOAFS算法参数与本文相同,IGOAFS算法中limit阈值设为15,随机个体选取量为种群规模的三分之一。3种算法的选择使得后文的对比实验中同时兼顾了横向和纵向的比较。 (1)平均分类准确率AAC AAC代表得到特征子集后,在特定数据集上利用分类器计算的平均分类准确率。AAC取值越大,代表分类性能越好。具体定义为 (21) 其中,M为实验重复次数,n为测试数据集的属性总量,Cj为属性j的正确分类标签,Lj为分类器得到的预测标签,函数Mat(x,y) 定义为 (22) (2)平均特征子集降低比例AFSR 由于原始数据集中包含许多非相关性的冗余特征,若特征子集中特征关联性不大,冗余特征过多,不仅会降低分类器的学习效率,还会降低数据集的分类准确率。因此,必须有效降低特征子集规模,最大程度提升特征间的相关性,在降低特征维度的同时,实现分类准确率的最大提升。 AFSR代表特征选择算法得到的特征子集规模降低程度。AFSR取值越小,性能越好。将平均特征子集规模AFS定义为 (23) 则AFSR为 (24) 其中,M为实验重复次数, |C| 为原始特征子集长度,g*,i为第i次算法运行的最优特征子集, |*| 为集合*的基数。 (3)平均适应度AF及标准差SD AF代表最优特征子集对应的平均适应度值,取值越小,算法性能越好。SD则体现特征选择算法的稳定性,取值越小,说明算法稳定性越强。具体定义为 (25) (26) 图6是4种算法在10个数据集上得到的平均分类准确率及相应标准方差值,柱状图对应左侧纵坐标,折线图对应右侧纵坐标。本文的LRGOAFS算法在Flare、Hepatitis、Ionoshpere、Wine、Zoo、Vote等6个数据集上得到了最高平均分类准确率,是4种算法中最好的。同时,LRGOAFS算法可以在规模较大的Flare上得到最高分类准确率,证明算法不仅可以处理中小规模特征选择问题,对较大规模特征选择也是有效可行的。标准方差对应算法稳定性,LRGOAFS算法在5个数据集上得到更小的标准方差,说明算法稳定性也比较好,在处理不同规模特征选择问题上适应度较强。另外3种算法虽然在个别数据集上可以得到比LRGOAFS算法更高的平均分类准确率,但稳定性欠佳,求解成功率太低。 图6 平均分类准确率 图7是4种算法在10个数据集上得到的平均适应度及相应标准方差值,柱状图对应左侧纵坐标,折线图对应右侧纵坐标。适应度函数(20)表明分类错误率越小,特征选择量越少,算法性能越好,对应于适应度函数值越小越好。可以看到,LRGOAFS算法在Bands、Ionoshpere、Lung、Wine、Zoo等5个数据集上得到了更小的适应度,是4种算法中占比最高的,说明在综合考虑分类准确率和特征选择量方面,算法具有更好的综合性能。也证实在LRGOAFS算法中采用针对标准GOA算法的改进措施是有效可行的,可以提升算法的寻优精度。 图7 平均适应度 图8 平均特征子集降低比例 图8是4种算法在10个数据集上得到的特征子集降维比例,比例越大,说明算法选择的最优特征子集规模越小,数据特征降维效果越好。LRGOAFS算法在6个数据集上得到最大降维比例,占比最高。结合图6的结果可知,LRGOAFS算法在Ionoshpere、Wine、Zoo、Vote等4个数据集上同时实现了最高的分类准确率和最小的特征选择比例,性能最好。另种3种算法并不能保证稳定性。 图9是4种算法在10个数据集上的平均计算时间对比结果。结果表明,LRGOAFS算法并不能保证在所有数据集上拥有最少的计算时间,甚至在部分数据集上计算时间花费更多(如Lung、Hepatitis数据集等),但结合前文算法在分类准确率(图6)、特征降维(图8)和适应度(图7)方面的表现,LRGOAFS算法依然实现了所有算法中的最佳综合性能,算法在特征降维、提升分类准确率的同时,并未牺牲过多计算效率。 图9 算法的平均计算时间 本文在第4节的实验配置阶段为LRGOAFS算法选用的分类器为KNN,这一部分进一步引用支持向量机SVM作为分类器对LRGOAFS算法的性能进行对比分析。KNN找到训练集中离预测样本点距离最近的k个值即可,在训练集和测试集规模很大时,预测效率很可观。且其参数只有一个k值,调参比较简单。SVM具有相对复杂的训练过程,训练完后再对测试集进行分类,两步独立进行。同时SVM参数更多,训练时间复杂性会略高。两种分类器各有优劣。将利用两种分类器的特征选择算法分别命名为LRGOAFS-KNN和LRGOAFS-SVM。测试了两种算法在平均分类准确率和平均特征子集降低比例上的实验结果,如图10所示。图中,柱状图对应左纵轴的平均分类准确率结果,折线图对应右纵轴的平均特征子集降低比例结果。由结果可知,LRGOAFS-KNN算法在6个数据集上的平均分类准确率是占优于LRGOAFS-SVM算法的,有一个数据集在这项指标上几乎接近。此外,LRGOAFS-KNN算法在7个数据集上的平均特征子集降低比例是占优于LRGOAFS-SVM算法的,LRGOAFS-SVM算法则有3个数据集。同时,结合两种指标的结果可知,LRGOAFS-KNN算法总共在6个数据集上同步实现了更高的分类准确率和更高的平均特征子集降低比例,说明在近选10组数据集的测试上,LRGOAFS-KNN算法的性能略优于LRGOAFS-SVM算法。 图10 KNN与SVM分类器间的比较 为了测试算法跳出局部最优的能力,利用一个多峰值基准函数Griewank进行寻优测试,函数表示如式(27)所示,函数的搜索区间为[-600,600],函数的理论极值为0。Griewank函数在整个搜索区间内存在多个极值点,因此可以测试算法是否具有跳离局部最优解的能力。依然选取前文灰狼优化算法BGWO[17]、蚱蜢优化算法BGOA[18]和改进蚱蜢优化算法IGOA[19]进行性能对比。结果如图11所示。首先,从寻优精度上看,在400次迭代过程中,LRGOA算法明显比另外3个算法可以得到更接近于理论极值点的解,说明其寻优精度更高。同时,曲线趋势上看,LRGOA算法具有明显的下坠趋势,而另外3种算法走势更平缓,说明寻优精度已经无法进一步提高。尤其在100次迭代至150次迭代中,LRGOA算法在某处停留后,有一个加快下坠的趋势,此处趋势可解释为:LRGOA在得到某局部最优解后,仍然可以跳离局部极值,进一步扩展到其他搜索空间得到更优解 (27) 图11 算法的寻优曲线 为了降维数据特征维度,提高数据分类准确率,提出了一种基于改进蚱蜢优化算法的特征选择算法。首先,利用融合完全随机性的混沌映射机制优化了蚱蜢初始种群,利用学习自动机对蚱蜢位置更新的调整系数进行改进,均衡全局搜索与局部开发;引入折射对立学习扩展搜索区域,避免算法过早陷入局部最优解,实现了改进蚱蜢优化算法。然后,将改进蚱蜢优化算法应用于数据集的特征选择求解,通过10种数据集测试验证该算法不仅降低特征维度,还可以提高数据分类准确率,且具有更好的稳定性。后续研究中,如何实现针对更高特征维度的特征选择以及如何实现蚱蜢优化算法的进一步优化是下一步的主要研究内容。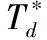
2 基于学习自动机和折射对立学习的改进蚱蜢优化算法LRGOA
2.1 基于混沌映射的种群初始化

2.2 基于学习自动机的调整系数c更新
2.3 基于折射对立学习的位置更新


2.4 LRGOA算法实现
3 基于LRGOA算法的特征选择方法LRGOAFS
3.1 特征选择模型


3.2 特征选择算法设计

4 实验分析
4.1 实验配置


4.2 评估指标
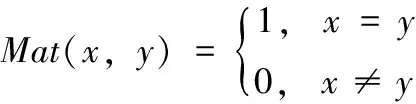
4.3 实验结果


5 结束语

