基于矩阵分解的上下文感知兴趣点推荐方法

李 旭，李景文,2+，姜建武,2，俞 娜

(1.桂林理工大学 测绘地理信息学院，广西 桂林 541006；2.桂林理工大学 广西空间信息与测绘重点实验室，广西 桂林 541006)

0 引 言

随着智能移动设备和信息技术的飞速发展，利用用户的签到信息为用户推荐心仪的兴趣点(point-of-interest，POI)已成为众多学者研究的重点内容[1,2]。POI推荐是根据用户的地理位置、访问时间和签到数据等一系列带有用户行为标签的上下文信息为用户推荐符合其个性化喜好的POI[3]，其不仅为学术界和工业界研究用户的个性化喜好和行为模式提供了新的切入点，还能帮助商家挖掘用户行为习惯，从而给商家带来巨大的经济效益[4]。然而，在实际应用中用户的签到记录与时间、地理位置和评论信息等因素密切相关，这些因素来自不同的领域，有不同的组成结构与表达方式，会对POI推荐造成不同程度的影响。因此，如何根据多种异构类型的上下文信息挖掘用户的潜在偏好，将时间、地理与用户个人偏好等因素融入到POI推荐模型中，为用户生成符合其个性化喜好的POI推荐列表，是POI个性化推荐服务的难点内容。

为了解决以上问题，本文提出一种基于矩阵分解的上下文感知兴趣点推荐方法，利用矩阵分解模型融合用户偏好、地理位置和访问时间等POI上下文信息，并通过随机梯度下降法优化矩阵分解模型的参数，从而提高POI推荐的准确度，满足不同用户的个性化喜好。

1 相关工作

近年来，已有大量学者对POI推荐技术进行了研究，大部分的POI推荐主要是利用各种推荐算法并结合上下文信息进行推荐。

在地理位置信息的应用方面，龚卫华等[5]通过分析用户的签到数据，发现用户的签到行为具有空间聚类现象，因此在POI推荐中特别强调地理影响力的作用，并通过矩阵分解对其进行建模。Zhang等[6]通过引入社会正则化和使用归一化函数来模拟社会影响和地理影响，并将其融入到矩阵分解模型中。在Zhang的基础上，Lian等[7]提出一种联合地理建模和基于隐式反馈的矩阵分解POI推荐模型，该模型利用二维核密度估计捕获用户移动数据中的空间聚类现象，有效缓解了POI数据的稀疏性，提高了POI推荐的准确性。Zhang等[8]提出一种对地理影响力进行建模的POI推荐方法，该方法考虑用户和POI的位置来模拟地理影响，并使用概率因子模型对其进行建模，可以更准确地预测用户在位置上的偏好，从而更好的对POI进行推荐。

在时间信息的利用方面，Ding等[9]为了研究评论文本中时间因素对用户选择POI的影响，提出了一种针对特定时间的时空距离度量嵌入模型(ST-DME)，该模型利用签入的时间和地理顺序属性来有效地建模用户对于特定时间的偏好。Yin等[10]针对POI推荐中信息过载问题，在协同过滤算法中融入时间因素，通过对用户进行聚类和建立时间遗忘曲线反映用户个性化喜好，从而提高算法运行的效率。原福永等[11]提出了一种融合时间序列的动态POI推荐算法，将地理位置与时间流行度相结合，预测POI的评分，从而提高POI推荐的准确性。

除了地理位置信息与访问时间信息，其它上下文信息对POI推荐也有着重要的影响。Yao等[12]利用高阶张量来融合社会上下文信息，并通过基于Tensor因式分解的协作过滤方法建模用户偏好。陈炯等[13]为提高POI推荐精度，综合考虑了社交、内容等多种POI上下文信息挖掘用户行为偏好。Ma等[14]通过分析用户的社交关系，提出一种具有社交正则化的矩阵分解框架，并取得了较好的推荐效果。

以上研究虽然在一定程度上考虑了上下文信息对POI推荐的影响，但只是通过协同过滤算法或者矩阵分解模型对上下文信息进行简单的线性组合，未充分挖掘用户之间的相互关系，并且缺乏对时间因素以及推荐多样性的统一分析，不能最大程度体现个性化推荐结果。

2 POI上下文信息建模

2.1 问题描述

对于特定的POI点，POI网络M表示POI点序列 ， 令U={u1,u2,…,u|u|} 表示一组用户，其中 |·| 为各自集合的基数。POI上下文信息可定义为一个三元组C=(D,G,T)， 其中矩阵D为用户偏好，G表示POI的地理位置，T为用户访问POI的时间。则POI个性化推荐问题可表述为在POI网络M中发现基于POI情景特征(G,T)、满足用户游玩偏好(D)的特定兴趣点集合。

2.2 融合时间序列的用户协同过滤推荐

表1 用户-POI偏好矩阵

传统的基于用户的协同过滤算法利用余弦相似度计算用户之间访问POI的相似性，本文在余弦相似度中引入时间变量，不同用户在相同时间访问同一兴趣点的频率越高，用户之间的相似度越高。其计算公式如式(1)所示

(1)

其中，sim(ui,t,uj) 表示用户ui与uj在t时间段访问POI的相似度，Num(ui,t,p) 表示用户ui在t时间段访问兴趣点p的次数，Num(uj,t,p) 表示用户uj在t时间段访问兴趣点p的次数。

令两个时间序列之间的相似性为所有用户Num(u)在任意两时刻之间相似度的平均值，时间ti与tj的相似度sim(ti,tj) 如式(2)所示

(2)

为了解决融入时间因素后带来的数据稀疏问题，增强时间序列的使用效率，提高POI的推荐效果，引入时间间隔d，使用平滑技术对时间相似度sim(ti,tj) 进行处理。用户ui在ti时刻访问兴趣点p的预测评分score(ui,ti,p) 如式(3)所示

(3)

根据式(1)、式(2)、式(3)，得到融合时间序列的用户之间相似度sim(ui,dt,uj) 如式(4)所示

(4)

融合时间序列基于用户的协同过滤算法的评分公式如式(5)所示

(5)

2.3 基于POI流行度的推荐

实际生活中用户访问POI时，热门POI是最先吸引用户关注的，只有在热度相对较高的POI中根据用户的喜好推荐相应的POI，才能更好达到个性化推荐效果。因此，本文提出POI流行度的概念，根据某个POI的用户访问人数及用户分享的POI的照片计算其受欢迎程度。某兴趣点pi的流行度计算公式如下

(6)

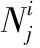
2.4 基于POI地理距离的推荐

在POI推荐的众多上下文信息中，POI的地理信息是进行推荐的核心内容。由地理学第一定律(Tobler’s First Law of Geography)可知：任何事物都有相关性，POI间距越小，用户访问的概率越大[15]。而在用户实际的访问轨迹中，发现用户对于POI位置的访问服从幂律分布。幂律分布如式(7)所示

f(x)=a×x-k

(7)

其中，f(x) 为概率密度函数，x为变量，a、k为参数。

基于幂律分布“POI离用户越近，用户访问概率越大；POI离用户越远，用户访问概率越小”的原则，将式(7)变为指数函数，得到式(8)如下

(8)

其中，simgeo(pi,pj) 表示兴趣点pi与pj之间的相似性，lat、lng分别表示兴趣点的纬度和经度，δ为距离调节因子，调整兴趣点间距离影响的大小。

2.5 基于POI最佳访问时间的推荐

在用户实际访问POI的过程中，大部分POI都有着明确的访问时间要求，并且不同的POI其访问时间要求也不同。比如，某POI规定在9:00～17:00这一时间段内用户能够访问，超出这个时间段则禁止用户访问。因此，针对POI访问时间的问题，本文提出了基于POI最佳访问时间的推荐。

(9)

其中，tmax表示POI禁止用户访问时间，tmin表示POI允许用户开始访问的时间。

3 融合上下文信息的矩阵分解模型

POI的个性化推荐是一个受多种因素影响的复杂的决策过程，用户的个性化偏好对于POI推荐的准确性起主导作用，但是用户所处场景的情景信息也对POI推荐有着至关重要的影响。本节提出一个融合上下文信息的矩阵分解模型(context-aware matrix factorization model，CAMF)，在融合用户偏好与情景信息对POI进行个性化推荐的同时，利用梯度下降法优化CAMF模型参数，从而更好拟合用户偏好和情景信息，提高POI推荐的准确性和个性化，为人们提供高效实时的智慧服务。

3.1 CAMF模型构建

图1为CAMF模型框架。CAMF模型将融合时间序列的协同过滤算法与基于POI流行度的推荐结合，体现用户自身偏好，其计算公式如下

(10)

图1 CAMF模型框架

根据用户自身偏好和POI地理位置、访问时间等情景信息，得到POI个性化评分如下

(11)

对于POI的个性化评分，利用CAMF模型对其进行求解，有效降低时间和空间上的复杂度。CAMF模型的目标函数如下

(12)

(13)

其中，yu,p为POI的真实评分。 Θ(U,P,T) 为正则表达式，防止目标函数L过拟合，U、P、T分别为用户u、兴趣点p和访问时间t的隐含特征矩阵。

3.2 CAMF模型优化

为了求得CAMF模型的最优解，本文采用随机梯度下降法来更新模型参数[16,17]。利用随机梯度下降法更新模型参数的训练过程如下

(14)

(15)

(16)

其中，γ是学习率，本文取0.001。

CAMF模型优化过程中，首先要对隐藏特征矩阵U，P，T进行初始化，然后对POI的上下文信息进行建模，得到用户偏好与POI情景信息的数学表示，最后利用矩阵分解模型融入用户偏好与POI情景信息，并利用随机梯度下降法得到最优的模型参数，从而获得POI的个性化推荐结果。CAMF模型具体的优化过程如算法1所示。

算法1：CAMF优化算法

输入：POI数据集R，用户-POI时间偏好矩阵D，照片数量N，学习率γ，调节因子α，β。

输出：隐含特征矩阵U，P，T

(1)初始化隐含特征矩阵U，P，T

(2)Repeat

(3)//计算POI个性化评分

(4) for u from 1：|U| do

(5) for i from 1：|P| do

(6)scoreU(ui,ti,p)←式(5)

(7)pop(pi)←式(6)

(8)simgeo(pi,pj)←式(8)

(11)//更新模型参数

(12) update {U,P,T}

(13) end

(14) end

2.运用有效方法，衔接算理和算法。处理算理与算法的关系注意：一是算理与算法是计算教学中有机统一的整体，算理和算法并重；二是算理教学需借助直观，引导学生经历自主探索、充分感悟的过程，要把握好算法提炼的时机和教学的“度”；三要防止算理与算法间出现断痕或硬性对接，必要时进行指导。

(15)Until 模型收敛

(16)ReturnU，P，T

4 实验与结果分析

4.1 实验数据集与预处理

从去哪儿网攻略库中爬取桂林的POI数据(http://travel.qunar.com/travelbook/list.htm?order=hot_heat)，数据集包括POI地理位置数据(经纬度)、用户分享的POI照片、用户访问时间数据和带有情感色彩的POI评论信息。

为使实验数据更加真实可靠，对实验数据集进行以下预处理：①删除分享照片数量少于5张和用户评论数少于2条的用户；②删除与评论信息不一致的照片；③构建用户-POI时间偏好矩阵。预处理后的实验数据集包含了2536位用户访问5676个POI分享的136 592条评论数据和252 327张照片，见表2。

4.2 推荐性能评价指标

本文采用推荐算法中最常用的评价指标准确率(precision@k)和召回率(recall@k)作为衡量算法推荐POI的性能。但是，仅根据准确率和召回率来判断算法推荐性能的优劣，具有一定的片面性。例如，推荐的POI集合中存在多个属于同一类型的POI，即使推荐的准确率和召回率较高，用户的个性化满意程度也不会太高。因此，为了避免推荐的景点重复，提高用户的个性化需求，在准确率和召回率之外，本文引入多样性(diversity@k)对推荐POI的类型进行评价。推荐性能评价指标定义如下

(17)

表2 预处理后的实验数据集

(18)

(19)

其中，pr表示推荐的POI集合，pu表示用户访问的POI集合。准确率和召回率的值越大，表明推荐的效果越好。typepr表示推荐POI集合中POI的种类，k为推荐POI集合中POI的数量。在准确率和召回率相差不大的情况下，POI多样性值越大，推荐的效果越好，用户对推荐的POI满意度越高。

4.3 调节因子的确定

由4.1节可知，POI个性化评分是由基于用户偏好与地理位置、访问时间等情景信息的评分公式融合得到的，而这种评分公式融合的关键在于调节因子α和β的取值。图2表示不同的α取值对基于用户需求的评分值的影响。从图2可知，α取值的变化对基于用户需求的评分值产生的影响并没有一定的规律性，不能准确判断出α取值对评分影响的优劣性。并且，若α取值过大，而用户的相似性又很低时，就会产生过度偏置；若α取值过小，用户对某POI分享的照片数量又很少时，也会对用户相似性很高的用户不公平。因此，本文采用式(20)对α的取值进行动态调整，以保证用户需求的合理性

(20)

其中，Num(pi) 表示用户访问兴趣点pi的次数，N(pi) 表示用户分享的照片数量。

图2 不同α值对POI得分的影响

调节因子β用来确定POI推荐时用户偏好与情景信息的权重分配。在推荐个数、调节因子α不变的情况下，不同β值对推荐准确率与召回率的影响如图3所示。

图3 β值对推荐性能的影响

β=0时表示只考虑POI情景信息的推荐，β=1时表示只考虑用户偏好的推荐。从图3可以看出，当β从0到1逐渐变化时，POI推荐的准确率和召回率会逐渐升高，达到一个最高值后又逐渐降低，这说明进行POI推荐时综合考虑用户偏好与POI情景信息比单纯只考虑其中一方面的推荐效果都好。随着β值的不断变化，推荐准确率与召回率的下降趋势比上升趋势要平缓一些，这说明随着生活质量的提高，用户的个性化需求在POI推荐中占据着越来越重要的地位，且当β=0.6时，POI推荐的准确率与召回率达到最大值，即用户偏好的权重值为0.6，POI情景信息的权重值为0.4时推荐效率最佳。

4.4 实验结果

4.4.1 影响因素分析

本文提出的CAMF模型融合了用户偏好、POI流行度、地理位置和时间等上下文信息，为了验证本文提出的CAMF模型的先进性，详细说明用户偏好、POI流行度、地理位置和时间这4种因素对POI推荐性能的影响程度大小，设计了4个简化的CAMF模型，分别移除其中一个影响因素对POI进行推荐，具体如下：

(1)CAMF-U：从CAMF模型中移除用户偏好特征；

(2)CAMF-P：从CAMF模型中移除POI流行度特征；

(3)CAMF-E：从CAMF模型中移除地理位置特征；

(4)CAMF-T：从CAMF模型中移除时间特征。

将这4个模型与CAMF模型在数据集上进行实验，设置POI推荐个数N为3、5、7、10，使用准确率和召回率作为评价指标来判断各个模型的推荐效果。实验结果如图4和图5所示。

图4 不同上下文因素推荐准确率对比

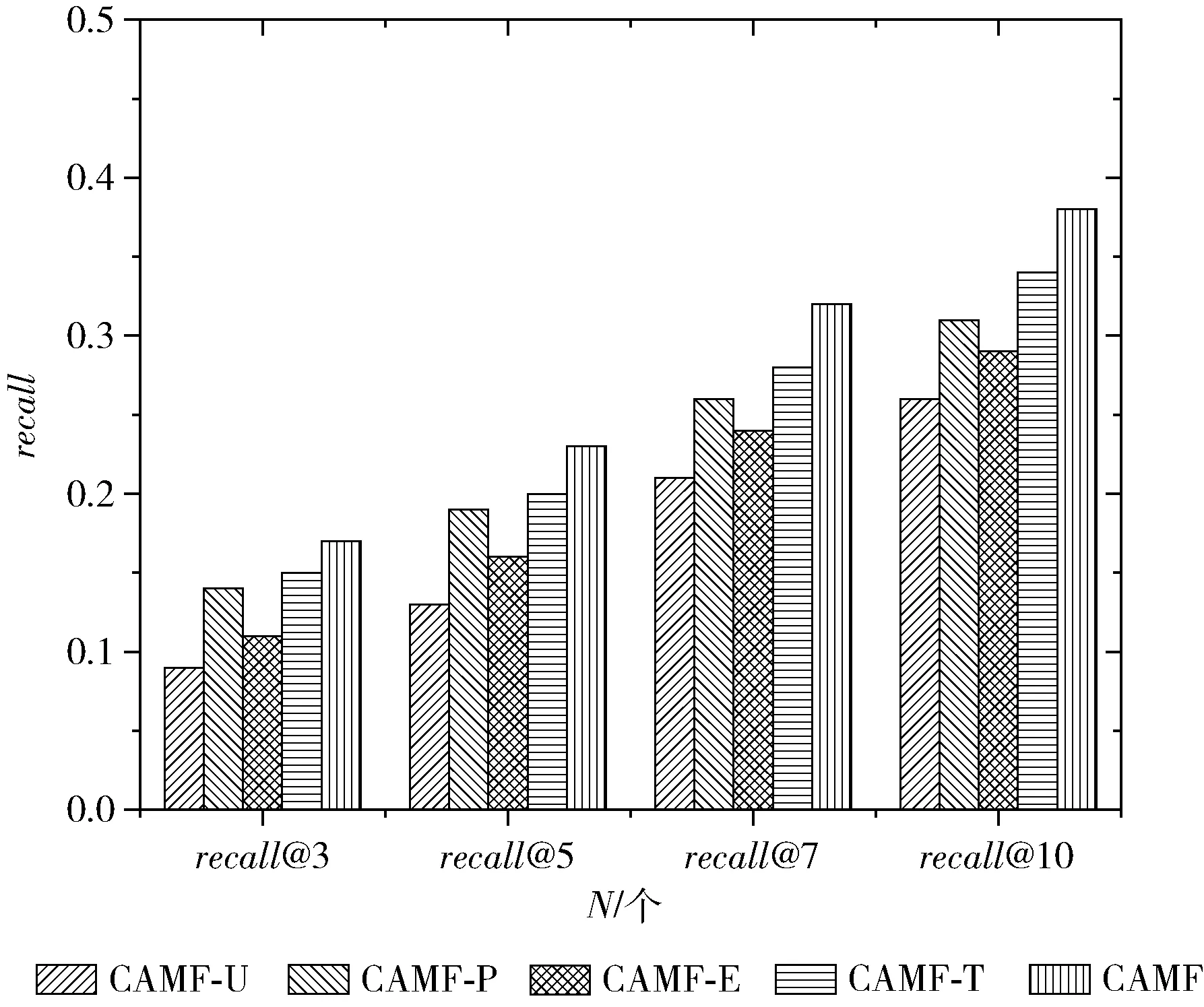
图5 不同上下文因素推荐召回率对比

从图4和图5可以看出，在POI推荐个数确定的情况下，CAMF模型的推荐效果好于其它4种模型，这说明融合用户偏好和其它上下文信息有助于提高POI的推荐性能。并且，用户偏好、POI流行度、地理位置和时间这4种因素对POI推荐的影响程度为：用户偏好>地理位置>POI流行度>时间。具体地说，虽然地理位置、POI流行度等上下文信息都能影响用户的签到行为，提高POI的推荐效果，但随着国民经济和通讯技术的飞速发展，用户自身偏好已成为POI推荐的决定性因素，对POI推荐准确率和召回率的提高有着至关重要的影响，因此用户偏好对POI推荐的影响最大。其次，由于POI推荐的特殊性，地理位置会极大限制用户对于POI的访问，用户会倾向于访问活动范围之内的POI，这也与地理学第一定律[15]得出的结论一致。由于用户对于POI的访问并没有严格的时间限制，并且可能因为某些用户故意错开一些高峰的时间点，从而使CAMF模型学习时间特征时产生偏差，因此，POI时间因素对POI推荐性能的影响最小。

4.4.2 算法性能比较

为了更好地展现CAMF模型的推荐效果，将CAMF模型与下列主流POI的推荐算法进行对比：

(1)PMF[18]：根据用户的评分数据，利用概率矩阵分解模型对兴趣点进行推荐。

(2)Rank-geoFM[7]：同时考虑时间上下文和地理影响，并将其融入到排序的矩阵分解模型中对兴趣点进行推荐。

(3)UTPG[11]：将基于用户的协同过滤算法与地理位置和时间流行度相结合，预测POI的评分，从而提高POI推荐的准确性。

(4)GSRT[13]：综合考虑了社交、内容、地理和时间等多种POI上下文信息挖掘用户行为偏好，并采用乘法法则进行融合从而对兴趣点进行推荐。

本文数据集中用户一天访问的POI大多在10个以下，因此设定推荐POI个数N为3、5、7、10。图6和图7给出了5个算法在推荐不同数量POI时准确率和召回率的变化情况。整体而言，随着POI推荐个数的增加，各种算法的推荐准确率会降低，这是因为POI推荐数量的增多会增加用户与时间的复杂性和POI地理位置的多样性；但POI推荐的召回率会提高，这是因为虽然POI推荐数量的增多了，但用户访问过POI的数量却没变。

图6 不同算法准确率对比

从图6和图7可以看出，在推荐POI个数确定的情况下，PMF模型的推荐准确率和召回率都最低，因为其只通过用户的评分数据进行POI推荐，没有充分考虑上下文信息。Rank-geoFM模型融合了时间上下文和地理位置影响，但由于未充分学习用户偏好，导致其推荐效果不佳。GSRT模型融合了社交、内容、地理和时间等多种POI上下文信息挖掘用户行为偏好，重现了用户访问POI时的情景，但其采用乘法法则对上下文信息进行融合，限制了其推荐性能。UTPG模型不仅融合了时间上下文和地理影响，还基于用户的协同过滤算法来学习用户和POI的特征矩阵，充分考虑了用户偏好在POI推荐中的影响。因此，UTPG模型相对于PMF、Rank-geoFM和GSRT模型，有着更好的推荐效果。

本文提出的CAMF模型无论在准确率还是召回率上都高于其它的POI推荐算法，并且在推荐个数逐渐增多时，其优势更加明显。这是因为CAMF模型成功地利用矩阵分解模型将用户的个性化偏好和地理位置、访问时间等情景因素结合起来，缓解了数据稀疏性，能够捕捉到兴趣点静特征之间的潜在关联，使得为用户推荐的POI更加的科学准确。

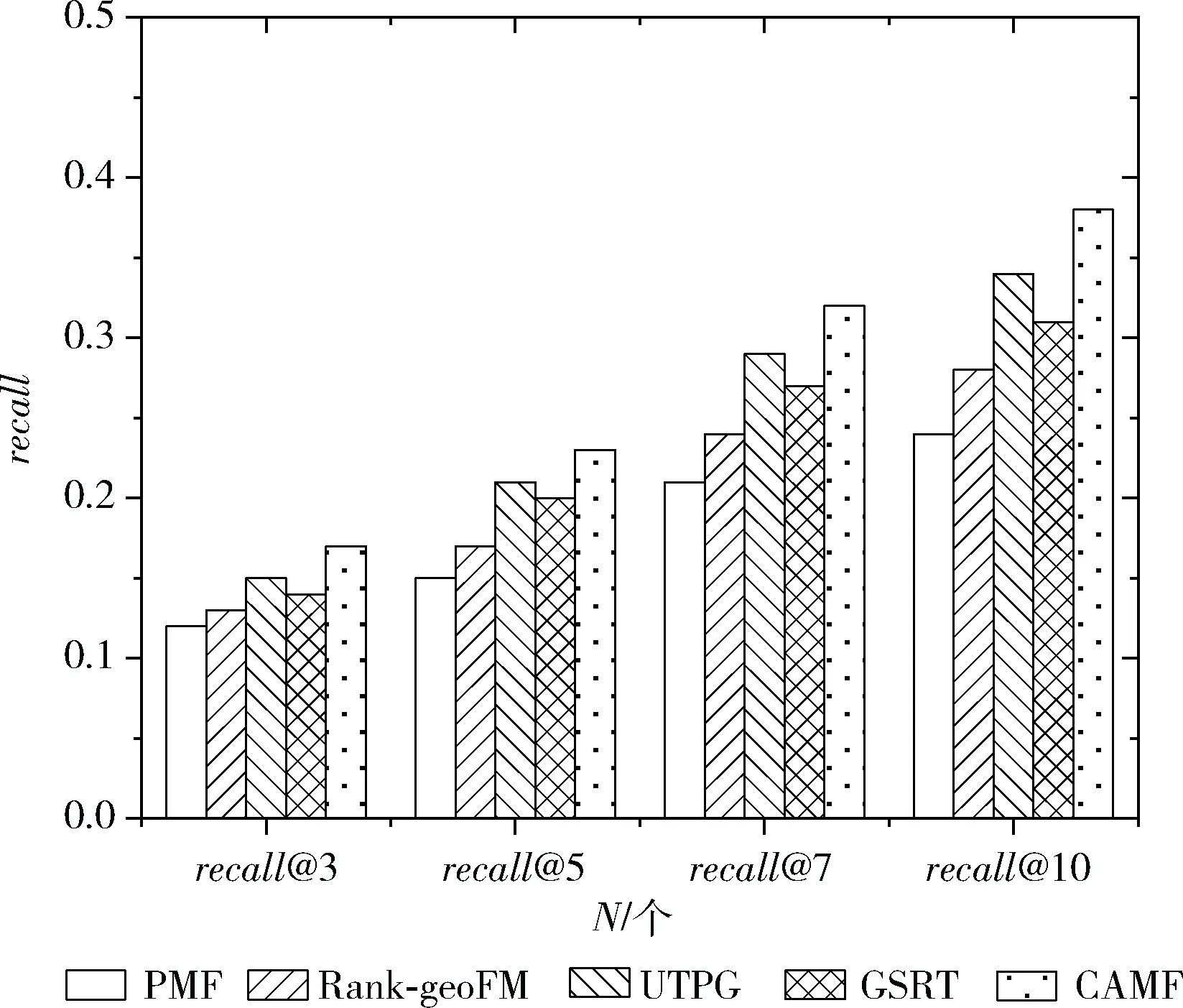
图7 不同算法召回率对比

4.4.3 推荐结果多样性评估

为了对多样性评估式(19)进行说明，本文假定从桂林火车站(25.2670,110.2898)出发，设置推荐个数k=5，距离调节因子δ=0.7，β=0.6。根据表2中的实验数据，得到各POI的类别和评分见表3。

表3 POI类别与得分

根据为用户推荐得分最高的POI的算法规则，可以得到为用户u1推荐的POI集合为G1={独秀峰王城景区，漓江，芦笛岩，银子岩，阳朔西街}，G2={独秀峰王城景区，漓江，银子岩，图腾古道，阳朔西街}。 从表3可知，这两个POI集合的评分只相差0.0095分，很难通过得分的高低判断哪个POI集合更能符合用户需求，因此需要对POI集合进行多样性分析。根据POI多样性计算公式(19)，得到POI集合的多样性得分如下：

diversity(G1)@5=-(1/5×log51/5+1/5×log51/5+2/5×log52/5+1/5×log51/5)=0.8277

diversity(G2)@5=-(1/5×log51/5+1/5×log51/5+1/5×log51/5+1/5×log51/5+1/5×log51/5)=1

因为diversity(G2)@5>diversity(G1)@5， 所以我们认为第二个POI集合更符合用户的个性化需求，为用户推荐的POI集合为G2={独秀峰王城景区，漓江，银子岩，图腾古道，阳朔西街}。

5 结束语

本文提出一种基于矩阵分解的上下文感知兴趣点推荐方法，在基于用户的协同过滤算法中融入时间序列，有效缓解了数据的稀疏性。通过利用CAMF模型融合不同的上下文信息，能更好建模用户的个人偏好和访问情景，并利用随机梯度下降法更新CAMF的模型参数，提高了模型的运行效率。最后，在去哪儿网获取的数据集中进行了实验，结果表明本文提出模型比其它主流的POI推荐算法有着更高的准确率和召回率，能满足用户的不同需求。在未来的工作中，将对上下文信息的提取与融合做进一步研究，以便提高推荐的准确性与满意度。