基于关联规则与知识追踪的编程题目推荐算法

向程冠，周东波，李 雷，王 英

(1.华中师范大学 教育大数据应用技术国家工程实验室，湖北 武汉 430079；2.贵州师范学院 数学与大数据学院，贵州 贵阳 550018)

0 引 言

编程题目推荐是在线编程教学平台不可缺少的智能导学功能之一，但目前大多数的在线编程教学平台还停留在教师传统课堂的网络化时空延伸，缺乏智能，只是起到连接师生的作用，教师可以给学生安排编程练习或考试，但针对学生个性化差异的智能导学功能薄弱，缺少针对编程题目推荐的服务，并未很好发挥对学习者学习行为分析、学习意图理解、学习状态追踪的作用，很难实现真正意义上的自适应学习诊断与有效学习。因此，通过学习者做题情况推荐新的编程题目成为了编程教育智能导学的研究热点之一。针对编程题目的特殊性与传统推荐算法的缺点，提出一种基于关联规则与知识追踪的编程题目推荐算法。

1 相关工作

个性化题目推荐是智能教育领域中的重要问题之一[1]。通过计算学生做题的历史数据或用户特征数据，给用户推荐合乎规则的题目，以达到个性化的智能导学服务。题目推荐时大多采用基于协同过滤、基于认知诊断与知识追踪的推荐算法，然而基于协同过滤的算法忽略了题目之间的关联信息，难以保证所推荐题目的解释性与合理性。认知诊断与知识追踪的方法通过计算学生对知识点的掌握情况，预测待推荐题目的得分情况，但忽略了学生学习行为的共性，难以将隐藏的潜在属性加入计算中，极易产生推荐误差。

Raciel Yera等提出了一种基于问题记忆的协同过滤算法[2]，用问题矩阵记录学生解决问题时失败的信息，从而为学生推荐编程题目，但未记录问题与知识点之间的关联信息，不能判断学习者是否已经掌握知识点，反复推荐题目，浪费了学习者宝贵的学习时间。马骁睿等提出了一种结合深度知识追踪的个性化习题推荐方法[3]，然而忽略了学习者学习行为过程，未考虑学习过程中推荐拔高题或巩固题。Avi Segal等提出了一种将协同过滤与投票相结合的教学内容个性化排序算法[4]，通过协同过滤算法计算相似学生在分数、重试次数和解题时间方面的难度排名，从而预测学生的难度排名，给学生定制个性化的试题，但忽略了学生对知识点的掌握状态。黄振亚提出了一种融合题目语义的知识追踪框架[5]，挖掘题目内容的个性特征对学生学习行为过程的影响，并在英语与数学题目上作了验证，但对于编程题目却很难从题目描述层面判断题目间的关联性。柏茂林通过计算能力水平相近的用户组，将kNN协同过滤算法应用于数学习题的个性化推荐中[6]。Surya Kant等提出了基于用户和项目的协同过滤算法[7]，通过计算用户相似度与项目相似度进行推荐。万永权等提出反馈式个性化试题推荐方法[8]，从试题难度与认知层次进行标准化，构造能力矩阵计算学生的能力进行试题推荐，但只能应用于客观题，不能应用于编程题目的推荐中。

知识追踪通过历史数据实时追踪学习者对知识掌握状态的变化，并预测学习者在未来学习中的表现，目前流行的知识追踪方法主要有贝叶斯知识追踪(BKT)模型与基于循环神经网络的深度知识追踪(DKT)模型[9,10]，BKT只是将知识的掌握情况简单分为“掌握”与“未掌握”，忽略了学习过程，而DKT模型只能对学习者整个知识水平建模，不能反映学习者对各个知识点的掌握情况。Jiani Zhang等提出了基于记忆网络的DKVMN模型[11]，用值矩阵表示学习者对各个知识点的掌握情况，并记录题目与各知识点的依赖关系，从而追踪学习者对各知识点的掌握情况，取得了良好的应用效果，但忽略了学习者遗忘行为对知识点掌握的真实影响。Fangzhe Ai等在DKVMN模型的基础上，加入了知识点的包含关系，改良了记忆矩阵[12]。李晓光等研究者提出了学习与遗忘融合的深度知识追踪模型[13]，考虑了遗忘行为对知识追踪影响，取得了较好的预测性能。

编程能力是计算机相关专业的学生应具备的关键能力之一，编程能力水平主要体现在完成编程题目的得分情况，学习者对于编程的学习过程不是简单的“对”与“错”，一道编程题往往要经过多次提交与反复修改才能完成，见表1，学习者完成一道程序题尝试提交了10次。因此，直接使用传统的个性化题目推荐算法推荐编程题目是不合适的。同时，在推荐题目时不考虑学生对知识点的掌握状态，不断推荐题目将会浪费学习者宝贵的时间。

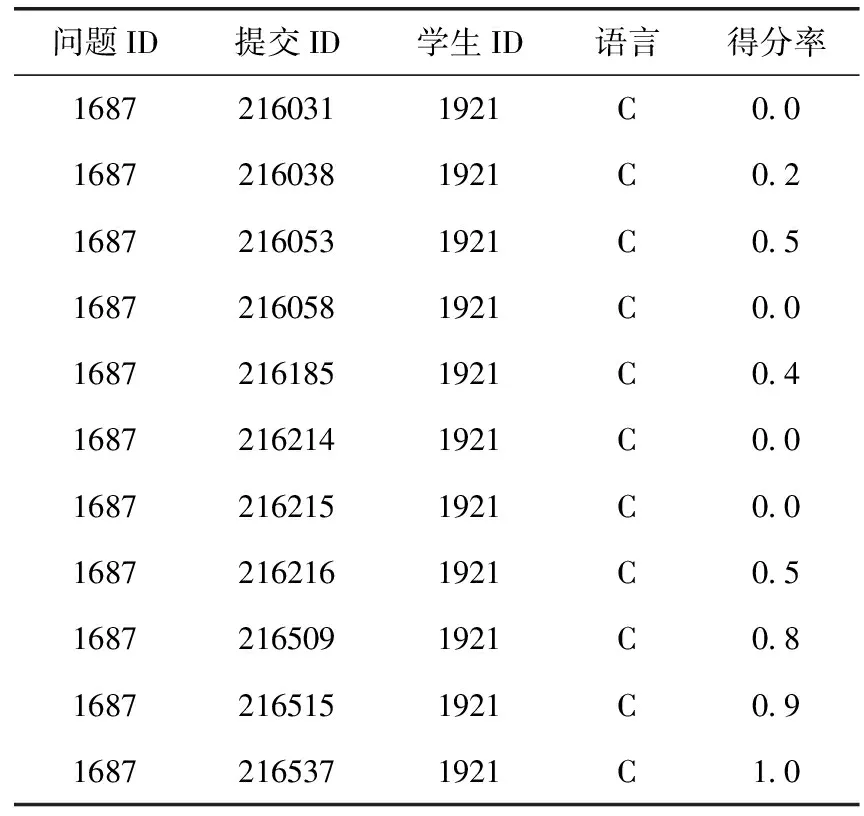
表1 编程题目提交列表

针对现有算法在编程题目推荐中的缺点，结合编程题特点，考虑学习者的遗忘规律特征，本文提出了一种基于关联规则与知识追踪的编程题目推荐算法，将关联规则挖掘与知识追踪结合起来，按提交次数阈值，把同一学习者在同一知识点下同时做对或做错的题目组成交易记录，从而挖掘出推荐规则，通过知识追踪模型计算学习者对知识点的掌握情况，决定推荐巩固题、拔高题或下一知识点的题目。

2 编程题目推荐算法

在编程题目推荐时，如果学习者已经掌握了当前知识点，就应该推荐下一个知识点的题目，否则应根据学习者的学习状态，决定推荐巩固题或者拔高题，以免浪费学习时间，提高学习效率。因此，在设计推荐算法时需要解决两个关键问题：

(1)如何计算推荐巩固题或拔高题？

(2)如何计算学习者对知识点的掌握情况？

对于问题(1)，考虑将同一学习者在同一个知识点下，尝试提交次数超过给定阈值时同时做错、同时做对的题目组成交易数据库，根据知识点的顺序关系，使用关联规则算法挖掘出推荐规则，对于尝试提交次数超过给定阈值的学习者推荐巩固题，尝试次数小于阈值时推荐拔高题，直到学习者掌握当前知识点时，推荐下一知识点的题目，学习者不需要做完当前知识点下的所有题目。

对于问题(2)，考虑编程题目的特殊性与学习者遗忘规律，不能只是简单地从结果的“对”与“错”来评估学习者对知识点的掌握情况，虽然DKVMN模型可以通过记录题目与各知识点的依赖关系，从而追踪学习者对各知识点的掌握情况，然而没有考虑到学习者的遗忘规律，也不适合编程题目的特殊性。在编程题目推荐算法时，先用DKVMN模型计算出学习者对知识点的掌握情况，再联合使用判别分析模型，从编程题目的特殊性与学习者遗忘规律的维度评估学习者对知识点的掌握情况。

2.1 关联规则挖掘

编程题目推荐时，可根据学生完成题目x的情况推荐题目集 {y1,y2,…,yn} (由n个巩固题或拔高题组成的集合)，x与yi(1≤i≤n) 是二元的推荐关系，不考虑yi与yj之间是否有推荐关系 (i≠j, 1≤i≤n, 1≤j≤n)。 因此，用关联规则挖掘题目之间满足规则的二阶大项集。

关联规则作为数据挖掘中的研究热点之一，用于挖掘数据间隐含的、未知的、有价值的关联性[14]。Agrawal等提出了关联规则挖掘的Apriori算法与AprioriTid算法[15]，使用上一次生成的大项集作为生成新候选项集的数据基础，达到剪枝的目的，提高算法的执行效率。其优点是在首次计算大项集时扫描交易数据库，以后每次用得到的候选项集构造k阶TID表，由k阶TID表生成k+1阶候选项集，除了在算法的开始阶段，所构造的TID表都要比交易数据库小，从而减少数据扫描次数。可其缺点是在开始阶段生成的TID表数据量有可能比交易数据库大，存储了k阶TID表中下一次计算k+1阶候选项集时不用的噪声交易项，增加了扫描次数，造成了不必要的I/O操作。针对上述缺点，算法改进的关键在于减少I/O操作与压缩数据量[16]，因编程题目推荐时需要计算二阶大项集，正处于AprioriTid算法的开始阶段，本文提出了一种AprioriTid的改进算法，用于计算题目集的二阶大项集。

性质1 A、B为题目构成的两个交易集合，若A是B的子集，则A的范数不大于B的范数。反之，若A的范数大于B的范数，A必然不是B的子集。

性质2 当k>1时，k阶候选项集一定是k-1阶候选项集的子集，那么k阶候选项集的元素一定取自于k-1阶候选项集。

算法改进的基本思想：由性质1、性质2可知，k+1阶候选项集是k阶候选项集的子集，它的生成依赖于k阶TID表，在构造k阶TID表时，先计算k阶大项集的幂集，再计算当前交易项与k阶大项集幂集的交集，如果交集的范数大于k，则将交集写入k阶TID表中，可极大减少k阶TID表的记录数，故而减少计算k+1阶候选项集时的数据扫描量与I/O操作，TID表记录数不可能比交易数据库大，可让算法在执行效率上得到明显优化。

用伪代码描述改进后的AprioriTid 算法如下：

(1)扫描题目构成的交易数据库D生成L[1];

(2)TID[1]=D;//1阶TID表就是交易数据库D

(3)for(k=2;L[k-1] !=null&&TID[k-1]!=null;k++){

(4)C[k]=Apriori_gen(L[k-1]);

(5) //使用Apriori_gen生成k阶候选项集

(6) TID[k]=null;

(7) foreach(tin TID[k-1]){

(8) foreach(cinC[k])if(cint)c.Sup=c.Sup+1;

(9)L[k]=null;

(10) foreach(cinC[k])if(c.Sup≥Minsup)L[k]=L[k]+c;

(11)M=PowerSet(L[k]);//计算L[k]的幂集

(12)MT=t.item∩M;//交易项与候选项集幂集的交集

(13) if(MT!=null&&|MT|>k){//|MT|>k的项写入TID[k]

(14)p.id=t.id;

(15)p.item=MT;

(16) TID[k]=TID[k]+p;

(17) //加入k阶TID表， 包含交易id与交易项

(18) }

(19) }

(20)}

表2给出了上述算法中所涉及的符号及描述。

表2 算法中的符号及描述

例：现有交易数据库D，见表3，设最小支持数为3，计算候选项集与大项集。

表3 交易数据库D

C[1]={{A},{B},{C},{D},{E},{F},{G}}，L[1]={{A},{B},{C},{D},{E}}，L[1]的幂集M={A,B,C,D,E}， 求M与每个交易项的交集MT， |MT|>1时写入TID[1]中。由TID[1]生成C[2]={{A,B},{A,C},{A,D},{A,E},{B,C},{B,D},{B,E},{C,D},{C,E},{D,E}}，L[2]={{A,B},{A,C},{A,D},{B,C},{B,D},{C,D},{D,E}}，L[2] 的幂集M={A,B,C,D,E}， 求M与每个交易项的交集MT， |MT|>2时写入TID[2]中。迭代算法直到TID为空时结束，算法过程如图1所示。

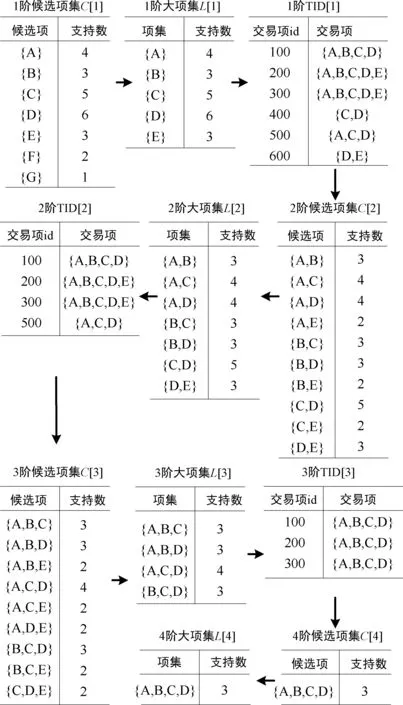
图1 改进的AprioriTid算法过程

2.2 基于知识追踪的知识点掌握分析模型

题目推荐的目的是为了让学习者通过练习掌握知识，如果掌握了当前知识点，就应推荐下一知识点的题目。如果推荐时不考虑知识点掌握状态，不断为其推送当前知识点的题目显然是不合理的。对于编程题目，一道题目需要经过若干次反复修改与提交才能完成，在计算学习者对知识点的掌握情况时需要满足两个方面的要求：一是能反应学习者对当前知识点的掌握情况，二是要考虑编程题需要经过若干次反复修改与提交才能完成的特殊性，一般认为学习者对一道编程题目尝试提交次数越多，反应出学习者对知识点的掌握越不好。因此，考虑在DKVMN模型的基础上，加入学习者每次提交的状态、所用知识点及提交次数、学习间隔时间、上次提交时所用知识点间隔时间等行为特征，运用判别分析计算学习者学习行为对DKVMN模型预测结果的影响。

用GA表示掌握知识点，GB表示未掌握知识点。X(i) 表示学习者特征，X(1)表示尝试提交次数，X(2)表示课程学习间隔时间，X(3)表示同一知识点学习间隔时间。X(2)、X(3)属于学习者遗忘特征数据，根据德国心理学家艾宾浩斯遗忘曲线，学习间隔时间按间隔天数t分段计算，即

(1)

因此，学习者数据被分成两组： {X1i(A),X2i(A),X3i(A)|i≤n1} 与 {X1j(B),X2j(B),X3j(B)|j≤n2}，n1+n2为学习者人数。

下面给出求判别指标的过程[17]。

通过线性组合构造一个判别函数，用于判断学习者学习状态，判别函数为

Y=L(X1,X2,X3)=C1X1+C2X2+C3X3

其中，C1、C2、C3为判别系数。

对于GA，n1个学生共有3*n1条数据，其观测数据矩阵为

对于GB，n2个学生共有3*n2个数据，其观测数据矩阵为

判别函数Y可最大限度区分GA与GB两组状态。GA有n1个样本

i为1到n1的自然数。代入判别函数，可得

yi(A)=C1X1i(A)+C2X2i(A)+C3X3i(A)

GB有n2个样本

i为1到n2的自然数。代入判别函数，可得

yi(B)=C1X1i(B)+C2X2i(B)+C3X3i(B)

在判断学生是否掌握知识点时，将学习特征数据 {X(1),X(2),X(3)} 代入判别函数Y，如果Y的值大于等于yAB时判别为未掌握该知识点，否则判别为已掌握该知识点。

2.3 编程题目推荐算法步骤

针对编程题目的特点，按学习者尝试提交次数阈值把作答历史记录数据库划分为两个库，在提交次数小于等于阈值的数据库中，将同一学习者在同一知识点下同时做对或做错的题目组成交易项，使用关联规则挖掘出巩固题推荐规则。解决一道编程题目需要多次修改与提交，熟练掌握了知识点的学生解决编程题目的提交次数相对较少，可用掌握了知识点的学生在完成编程作业时的平均提交次数作为划分阈值。

同理，在提交次数大于阈值的数据库中，将同一学习者在同一知识点下同时做对或做错的题目组成交易项，挖掘出拔高题目推荐规则。推荐时考虑题目提交次数与学习者遗忘特征，使用知识追踪的DKVMN模型与判别分析模型计算学习者对当前知识点的掌握状态，决定推荐巩固题、拔高题或下一知识点的题目。

本文算法具体步骤如下：

步骤1 根据学习者做题历史记录，使用改进后的关联规则挖掘算法生成推荐规则。

步骤2 生成DKVMN模型。

步骤3 生成各知识点的判别函数Y与yAB。

步骤4 输入学生做题记录，由DKVMN模型评估学生是否通过当前知识点，未通过执行步骤6，否则执行步骤5。

步骤5 输入学生学习特征数据：题目提交次数、同一知识点学习间隔时间、课程学习间隔时间，并代入与判别函数Y，如果函数值大于等于yAB执行步骤6，否则执行步骤7。

步骤6 尝试提交次数超过给定阈值时推荐巩固题，尝试次数小于阈值时，推荐拔高题，执行步骤4。

步骤7 推荐下一知识点的题目。

3 实验评估

3.1 实验数据集

为了验证本文提出的编程题目推荐算法的可行性与有效性，采用某高校在线编程教学平台的实际生产数据进行实验，以C程序设计课程为对象，经过专家标注的知识点共124个，学生754人，程序提交1 358 973次，编程题目6230道。

算法实现采用Python语言编写，运行的硬件环境为Intel(R) Core(TM)i7-8550U CPU @1.80 GHz(8 CPUs)，16 G内存，操作系统为CentOS6。

3.2 评测指标选择

关联规则的改进算法评估从算法效率与精准性2个方面进行考量，算法效率从时间复杂度方面考量，精准性反映算法的可靠程度与可行性，它们是推荐算法可靠可行的基础保障。

题目推荐算法评价从题目推荐的覆盖率(Coverage)和准确率 (Precision)2个方面进行考量，覆盖率主要用于观察算法推荐的题目集合Prc与实际可推荐的题目集合Preal交集中题目数量占实际可推荐的题目比率，计算公式如下

(2)

准确率主要用于观察题目推荐算法的正确性与可行性，其计算方式为所推荐的准确题目所占推荐题目总数的百分比，值越大表示推荐算法的正确性越高，计算公式如下

(3)

3.3 实验结果与分析

3.3.1 改进的AprioriTid算法分析

算法效率分析：选取最小支持数为50，从1 358 973条提交记录中随机选择0.5 w、1 w、1.5 w、2 w、2.5 w、3 w、3.5 w和4 w进行对比测试，运行结果如图2所示。另外选取数据量为4.5 w，最小支持数分别为60、80、100、120、140、160、180和200进行对比测试，运行结果如图3所示。

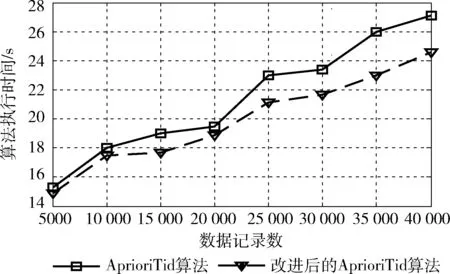
图2 最小支持数为50时两种算法的运行时间

图3 随最小支持数增大时执行效率比较

从图2、图3中可以看出，在最小支持数为50的情况下，改进后的AprioriTid算法比AprioriTid算法在时间性能上平均提升了1826 MS，当数据量增加到4 W时，改进后比改进前少用了2982 MS。在数据量不变的情况下，支持数由60增加到120时，改进后的AprioriTid算法在时间性能上平均提升了871 MS。

算法精准性分析：分别设置支持数为50、60、80、100、120、140、160、180和200，从1 358 973条提交记录中随机选择了10组数据对算法的准确率进行实验，数据量分别为2000、4000、6000、8000、10 000、12 000、14 000、16 000、18 000和20 000，用改进前后的AprioriTid算法分别生成大项集。实验结果表明，改进前后算法生成的大项集是一致的，究其原因主要在于k阶TID表是构造k+1阶候选项集的数据基础，计算k阶TID表时，先计算k阶大项集的幂集，再计算出当前交易项与k阶大项集幂集的交集，如果交集的元素个数小于等于k，便不可能产生k+1阶候选项集，并且k+1阶候选项集只能产生于k阶大项集中，通过计算交集可对不在k阶大项集中元素进行剪枝，并不影响计算k+1阶候选项集，故改进后的算法不会损耗原有算法的精准性。

3.3.2 编程题目推荐算法分析

在实验数据集上，设置题目提交尝试次数阈值为5，将实验数据集分为巩固题数据集(提交尝试次数小于等于5，共537 681条数据)与拔高题数据集(提交尝试次数大于5，共821 292条数据)。选取400名学生的期末考试数据，将考试中每个知识点的得分率超过0.8的学生划分到GA组，其他学生划分到GB组，统计学生平时练习的程序提交次数、知识点学习间隔时间与课程学习间隔时间3项学习者特征数据，生成各知识点的判别指标。设置关联规则挖掘的支持数为200，最多推荐题目数为20，在巩固题数据集与拔高题数据集上分别设置训练集/实验数据集为60%、70%、80%与90%的情况下，将本文算法与基于用户的协同过滤算法(UserCF)、kNN协同过滤算法[6]、BiUCF[7]进行10次对比实验取平均值，实验结果见表4、表5。

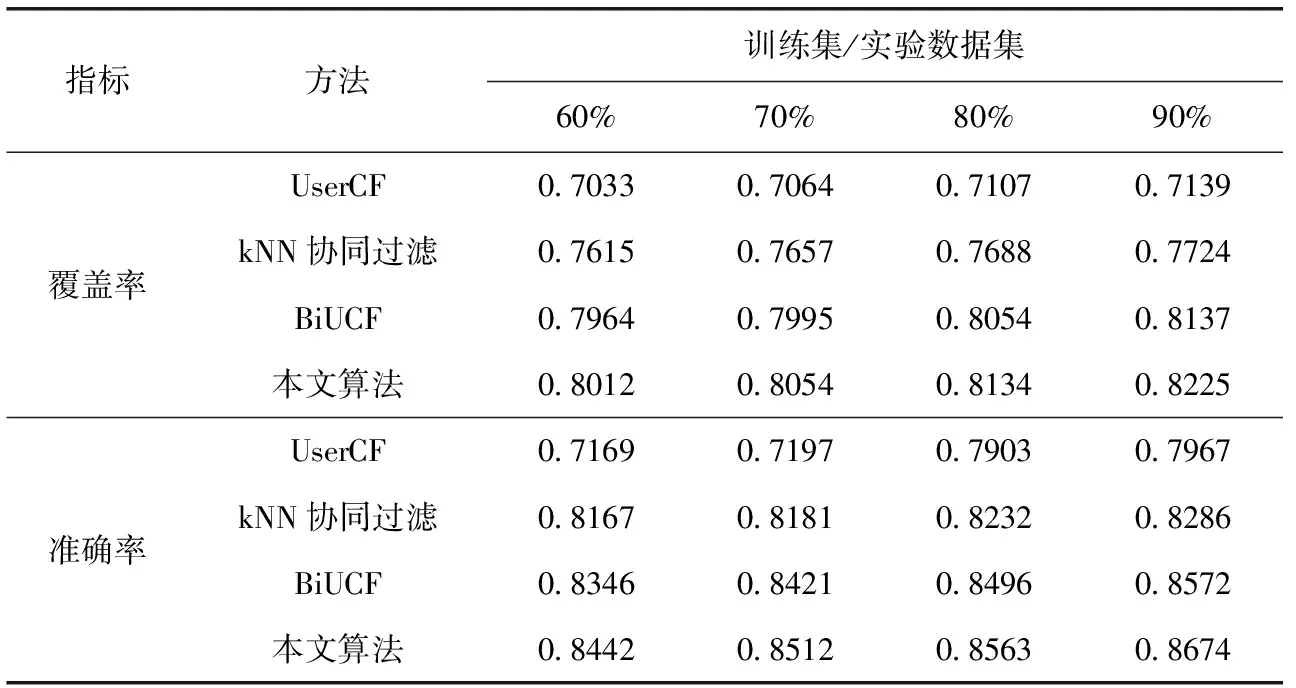
表4 巩固题推荐的覆盖率与准确率比较

在覆盖率与准确率2个指标上，本文提出的推荐算法在推荐巩固题与拔高题方面均优于其它3种推荐算法，原因在于本文算法考虑了编程题目的特征、学习者对知识点的掌握状态以及学习者遗忘特征。

4 结束语

本文提出了一种基于关联规则与知识追踪的编程题目推荐算法，算法根据编程题目的特点，使用关联规则挖掘出同一知识点下同一学习者在尝试提交一定次数后同时“做对”与“做错”的题目推荐规则，通过分析学习者的遗忘特征，使用知识追踪模型与判别分析模型计算学习者对知识点的掌握状态，决定推荐巩固题或拔高题，或进入下一知识点学习，从而优化学习者学习效率。实验结果表明，本文提出的推荐算法具有较好的推荐效果，并已成功应用于某高校的在线智慧教学平台中。

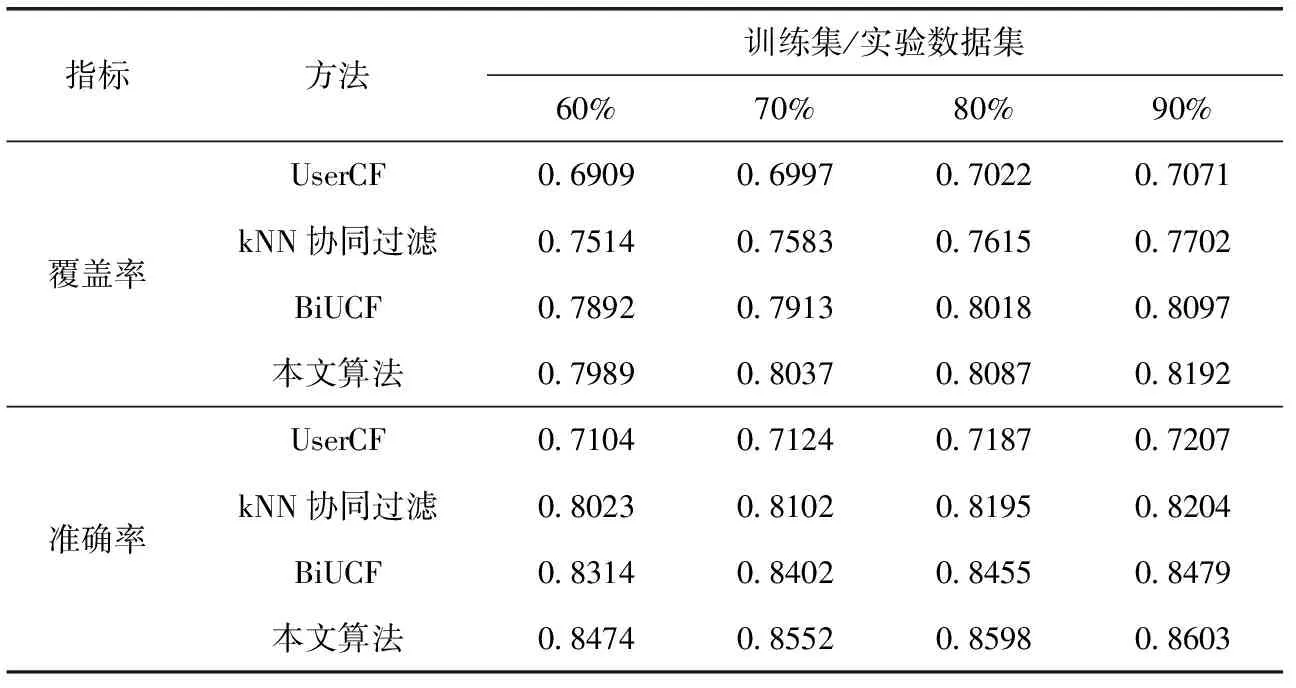
表5 拔高题推荐的覆盖率与准确率比较