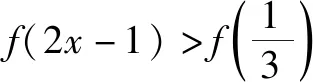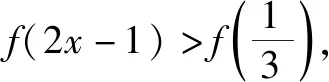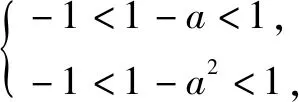变式训练在高一函数教学中的应用
甘肃省平凉市静宁县文萃中学 王永兵
变式训练是高中数学课堂培养学生自主探究学习的一种有效教学方式,尤其是高一新生在学习新概念、新公式、新定理以及解决数学问题过程中,进行不同角度、不同层次、不同情形、不同背景的变式训练,可以帮助学生深刻理解知识的本质,揭示不同知识点之间的内在联系,让学生轻松地建立起知识点之间的框架结构,促进学生认知发展,坦然面对各种复杂问题,有效解决问题[1].
在单一的例题教学中引入变式教学,可以拓展学生的解题思路,让学生更深刻地理解知识之间的联系,利用已有数学知识探究新题型解题之法.不同角度、不同层次、不同情形、不同背景的变式训练可以快速提升学生对知识的理解,通过合理恰当的变式训练,让学生深刻理解知识的本质,有变化的重复学习可以提升解题效率[2],加快该类题型模型化的程度.
1 利用变式训练强化学生的数学抽象素养
例1关于x的函数f(x),其定义域为(m,n),则b>0时,函数f(bx)的定义域为.
分析:函数的定义域是自变量x的取值范围,抽象函数f(x)和f(bx)之间因对应关系f建立起桥梁,把x换元为bx,其范围不变(即x的范围就是bx的范围),解不等式可解得函数f(bx)的定义域.这里要注意的是函数的自变量的范围经过括号内变换后范围不同.
解:因为函数f(x)的定义域为(m,n),所以函数f(bx)有意义时,则有m 变式1a>0时,函数f(ax)的定义域为(m,n),则函数f(x)的定义域为. 解:因为函数f(ax)的定义域为(m,n),且a>0,所以am 故函数f(x)有意义时,则有am 所以函数f(x)的定义域为(am,an). 变式2a>0时,函数f(ax)的定义域为(m,n),求函数f(bx)的定义域. 分析:变式2是例1和变式1的综合题. 解:因为函数f(ax)的定义域为(m,n),且a>0,所以am 故函数f(bx)有意义时,则有am 点评:如果一个函数是具体的,它的定义域学生不难理解,但对于一个没有具体解析式的抽象函数而言,其定义域就难以捉摸,变式训练可促进学生对抽象函数及其定义域的理解,从而掌握抽象函数定义域的求法.在对应关系f下进行变换的式子范围没有改变,主要体现换元思想,利用不等式求解不同抽象函数的定义域.抽象函数虽然定义域发生了改变,但是值域还是相同的.函数的定义域始终是自变量的取值范围,不管抽象函数的元怎么变,在同一对应关系下,其制约条件是一致的,即在同一取值范围内,通过换元求得不同函数的定义域,也可以结合函数的图象,平移伸缩变换说明定义域的变化过程. 例2若函数f(x)=ax2+bx+3a+b是偶函数,且定义域为[a-1,2a],则a=,b=. 变式已知f(x)是R上的奇函数,且当x>0时,f(x)=2x2-1,则f(-1)=,f(x)=. 分析:根据奇函数的定义可知,存在-x使得f(-x)=-f(x),所以f(-1)=-f(1)=-1.又函数在R上有定义,图象关于原点对称,所以满足f(0)=0. 解:由函数f(x)是奇函数,得f(-x)=-f(x). 所以f(-1)=-f(1)=-1. 设x<0,则-x>0,满足 f(-x)=2(-x)2-1. 所以-f(x)=2x2-1,即f(x)=1-2x2. 又因为函数在原点处有定义,所以f(0)=0. 点评:函数的奇偶性,考察函数图象关于原点和y轴的对称性.首先必须坚持定义域优先原则,定义域关于原点对称;其次根据函数为奇函数,有f(-x)=-f(x),若在x=0处有定义,则有f(0)=0.函数为偶函数有f(-x)=f(x),可求得函数的解析式以及参数的值. 变式函数f(x)是定义在(-1,1)上的奇函数,且为增函数,若f(1-a)+f(1-a2)>0,求实数a的取值范围. 其次函数f(x)为奇函数,则f(1-a)+f(1-a2)>0 变形为 f(1-a2)>f(a-1). 又因为函数在定义域上是增函数,所以1-a2>a-1,解得-2 综上,实数a的取值范围(0,1). 点评:变式教学可以促进新知识与已有知识之间建立联系,理解并掌握函数的单调性及其几何意义,让学生通过自主探究,体会数学概念的形成过程.偶函数在其对称的区间上有相反的单调性,奇函数在其对称的区间上有相同的单调性;通过变式训练让学生学会运用函数图象理解和研究函数的性质,利用单调性比较函数值的大小、解不等式、求最值等,帮助学生提高应用知识解决问题的能力. 综上所述,变式教学为学生巩固基础知识的同时创设求异思变的空间,启发学生透过不同现象看透数学问题的本质,探索数学规律和数学理论知识的内在联系,有利于帮助学生形成科学的概念,并对类型知识学习建立模型提供有力帮助.

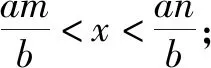
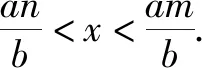

2 利用变式训练深化学生对基础知识的理解
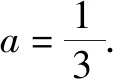
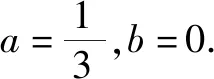
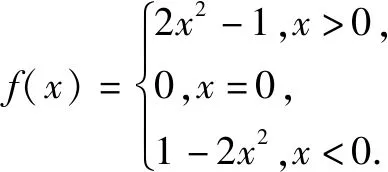
3 利用变式训练拓展学生的数学思维