合理换元 巧妙构建——一道导数题的探究

山东省菏泽第一中学 孟丽娟

1 问题呈现

问题[2022年安徽省安庆市高三模拟考试(二模)数学试题(理)·12]若存在两个正实数x，y使得等式x(2+lnx)=xlny-ay成立，则实数a的取值范围是( ).

此题以含参的方程为问题背景，利用等式成立创设情境，进而确定参数的取值范围.除了参数a外，还有两个对应的变量x，y，结合等式的转化并借助对数运算等加以恒等变形，对两个变量x，y之间的关系加以合理处理，是切入与解决问题的关键.

2 问题破解

方法1：比值换元法1.

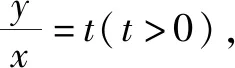
令f′(t)=0，解得t=e3.

当t∈(0，e3)时，f′(t)>0，函数f(t)在区间(0，e3)上单调递增；当t∈(e3，+∞)时，f′(t)<0，函数f(t)在区间(e3，+∞)上单调递减.

故选择答案：D.

解后反思：根据题目条件中对应等式的恒等变形，合理分离参数，巧妙换元，从而构建函数，利用函数的导数及其应用，通过函数的单调性与极值来确定参数的取值范围.利用比值进行巧妙的换元处理，为构建函数提供条件，从而转化为常规的函数问题来分析与处理.

方法2：比值换元法2.

故选择答案：D.

解后反思：根据题目条件中对应等式的不同视角的恒等变形，也同样可以进行比值换元，虽然换元视角不同，但解题思维一致.抓住常规思维，合理恒等变形，巧妙分离参数，正确构建函数，函数求导处理，单调极值确定，是解决此类问题中一系列基本的思维步骤与操作技巧.

方法3：多次换元法.

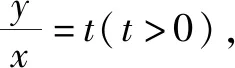
当m∈(0，e)时，f′(m)>0，函数f(m)在区间(0，e)上单调递增；当m∈(e，+∞)时，f′(m)<0，函数f(m)在区间(e，+∞)上单调递减.

故选择答案：D.

解后反思：根据题目条件中对应等式的恒等变形，巧妙分离参数，两次进行换元，其目的是进行齐次化处理，进而合理构建函数，同样利用导数来确定函数的最值，从而确定参数的取值范围.齐次化处理时要求学生具备较强的观察能力与数学运算能力，有时解题中数学运算量比较大.

3 变式拓展

将原题及其对应的解决技巧方法等从视角、深度、广度等方面加以思考与推广，才能进行多方位的认识与应用，从而充分体会与挖掘原题的训练与应用价值，得到对应的变式问题，进而进一步提升与拓展知识与能力.

变式1若存在两个正实数x，y使得等式2x+a·(y-2ex)(lny-lnx)=0成立，则实数a的取值范围为( ).

所以g(t)≥g(e)=-e.

故选择答案：C.

解后反思：根据函数与方程的关系将方程进行转化，利用换元法转化为方程有解，构造函数求函数的导数，利用函数极值和单调性的关系求解即可达到目的.合理分离参数，利用构造法和导数法求出函数的极值和最值是解决此类问题的关键.

变式2若存在两个正实数x，y使等式x+a(y-x)(lny-lnx)=0成立(其中e=2.71828…)，则实数a的取值范围是.

所以当t∈(0，1)时，g′(t)>0，函数g(t)单调递增；当t∈(1，+∞)，g′(t)<0，函数g(t)单调递减.

故g(t)在t=1时，取得最大值g(1)=0.

解后反思：根据题目条件合理变换对应的等式，巧妙换元与构建函数是破解问题的关键.借助求导来确定函数的单调性，进而确定对应函数的极值与最值是解决此类问题的目的，为进一步解决分离参数后所对应参数或参数关系式的取值范围提供条件.

4 教学启示

(1)通技通法，归纳总结

涉及等式或不等式恒成立背景下求解参数取值范围的问题，“通技通法”就是对相应的等式或不等式加以恒等变形与转化，合理构建对应的函数，利用函数的单调性与极值、最值来求解相应参数的取值范围.构建函数时，要借助整体换元思维、同构思维等.

(2)知识交汇，能力提升

涉及此类等式或不等式恒成立下的参数取值范围的问题，经常在知识的交汇处加以巧妙设置，充分考查不同知识点之间的交汇与融合，以及不同知识点与思想方法的综合与应用.解决问题时切入点多，技巧性强，思维方法多样.通过问题的深入分析与解决，巧妙形成知识体系，清晰解题思维，从而提升学生理解问题、分析问题与解决问题的能力，拓展数学品质，培养数学核心素养.