深度理解促思维灵活
——一道高考试题的多维探究及教学建议
甘肃省武威第八中学 张雪基
解三角形是高中数学的重要知识点,是高考考查的常见问题类型.《普通高中数学课程标准(2017年版2020年修订)》中,解三角形位于必修课程主题三,几何与代数,第一单元,平面向量及应用.要求借助向量的运算,探索三角形边长与角度的关系,掌握余弦定理、正弦定理;能用余弦定理、正弦定理解决简单的实际问题.角和边是三角形中的两类基本量,它们之间的关联由内角和定理、两边之和大于第三边、大边对大角、正余弦定理等构建.问题求解过程中还会涉及和差角、倍半角、和差化积、积化和差公式等三角变换工具.这些定理、公式的本质是什么?知识的背后又蕴含着怎样的策略、方法和思想?
笔者以一道高考试题为例,带着上述问题思考与探究,建议教师在教学中要让学生养成从基本概念和原理出发思考问题、解决问题的习惯,深度理解概念和原理的实质性联系,才能有效增强学生思维的灵活性、深刻性和反思性.
1 试题呈现
(2022年全国高考乙卷理科第17题)记△ABC的内角A,B,C的对边分别为a,b,c,已知sinC·sin(A-B)=sinBsin(C-A).
(1)证明:2a2=b2+c2;

2 解法探究及教学建议
2.1 第(1)问解法探究及教学建议
证法一:由sinCsin(A-B)=sinBsin(C-A)及和差角公式,得
sinCsinAcosB-sinCcosAsinB=sinBsinC·cosA-sinBcosCsinA.
由正弦定理,得
accosB-bccosA=bccosA-accosC.
由余弦定理,得
整理得a2=b2+c2-a2,故2a2=b2+c2成立.
教学建议:已知角的关系,证明边的关系,是这个问题的本质.正弦定理、余弦定理、大边对大角是三角形中最基本的边角关系,这些关系背后蕴含的基本策略,是把三角形中边与角的关系相互转化.正余弦定理教学时,应通过实例呈现两个定理的发生、发展和应用过程,让学生感受到两个定理在“边角互化”中的强大功能.
证法二:由sinCsin(A-B)=sinBsin(C-A),结合内角和定理、诱导公式,得
sin(A+B)sin(A-B)=sin(C+A)sin(C-A).
由和差角公式,得sin2Acos2B-cos2Asin2B=sin2Ccos2A-cos2Csin2A.
由同角三角函数基本关系式,得
sin2A(1-sin2B)-cos2Asin2B=sin2C(1-sin2A)-cos2Csin2A.
整理,得2sin2A=sin2B+sin2C.
由正弦定理得2a2=b2+c2成立.
教学建议:三角形内角和定理是小学内容,学生特别熟悉,但在解三角形问题中最容易被忽视,它是特别重要的角与角之间的关系,是角之间建立联系的有效途径.而和差角公式、诱导公式、同角三角函数基本关系式则是解三角形的必备工具.由2sin2A=sin2B+sin2C获得2a2=b2+c2的过程,背后蕴含着正弦定理“边角”互化的转化思想及形式“统一”的思维.
证法三:由sinCsin(A-B)=sinBsin(C-A),结合内角和定理、诱导公式,得
sin(A+B)sin(A-B)=sin(C+A)sin(C-A).
由积化和差公式,得
即cos 2B+cos 2C=2cos 2A.
由余弦的二倍角公式,得
1-2sin2B+1-2sin2C=2(1-2sin2A).
即2sin2A=sin2B+sin2C.
由正弦定理得2a2=b2+c2成立.
教学建议:“和差化积”与“积化和差”公式常被教师们认为“无需掌握”,笔者认为它们本质上是“和差角”公式的外延,有必要让学生在实际问题的解决过程中体会其功能.实际上,《普通高中数学课程标准(2017年版2020年修订)》明确要求学生能够推导出两组公式,但不要求记忆,2019年版北师大教材中,单独列出一节讲述这部分内容.
证法四:由sinCsin(A-B)=sinBsin(C-A)及差角公式,得sinCsinAcosB-sinCcosAsinB=sinBsinCcosA-sinBcosCsinA.
整理,得
sinA(sinCcosB+cosCsinB)=2sinB·sinCcosA.
逆用正弦的和角公式,得
sinAsin(B+C)=2sinBsinCcosA.
由内角和定理及诱导公式,得
sin2A=2sinBsinCcosA.
由正弦定理,得a2=2bccosA.
所以2a2=b2+c2成立.
教学建议:相较于证法一,证法四用差角公式展开后并没有直接利用正弦定理把获得的式子转化为边角混合式,而是冷静观察代数式的结构,将其转化为sinA(sinCcosB+cosCsinB)=2sinBsinCcosA,体现出对结构式的整体把握,以及对正弦和角公式的深度理解.三角变换涉及到和差角公式、诱导公式、同角三角函数基本关系式、倍半角公式等.公式教学不能“一个公式、三点注意”就草草了事,应在公式为什么会有?怎样来?结构是怎样的?与其他公式有何关系?有什么核心功能?等这些核心问题上下功夫.能够准确回答上述问题,应用时才能得心应手.
证法五:在△ABC中,sinCsin(A-B)=sinB·sin(C-A),sinC≠0且sinB≠0.
若sin(A-B)=0,则sin(C-A)=0,有A=B且C=A成立,即A=B=C,所以a=b=c.
此时2a2=b2+c2成立.
若sin(A-B)≠0,则sin(C-A)≠0,由sinC·sin(A-B)=sinBsin(C-A),得
整理,得
2bccosA=a(ccosB+bcosC).
由余弦定理,得
所以2a2=b2+c2成立.
教学建议:三角形中内角对应的三角函数值除具有一般三角函数的性质,还具有其特殊性,如sinC≠0且sinB≠0正是基于三角形的特征获得,要适时让学生认清“特殊”和“一般”的关系.这种证法看似冗杂,且最后又回到正余弦定理的应用上去,但学生在实际探究中,常会出现这种想法,教师应鼓励学生多角度思考问题.方法的多样性能够增强学生对问题认识的深刻性,更能有效增强学生思维的灵活性.
2.2 第(2)问解法探究及教学建义
解法一:由⑴知2a2=b2+c2,又a=5,所以
b2+c2=50.

所以(b+c)2=b2+c2+2bc=81,故b+c=9.
所以△ABC的周长为a+b+c=14.
教学建议:“整体”观是此法和下述两种方法中的一种最基本的观念,这种观念源于对余弦定理结构式的整体把握和深度理解,有了这种观念才能把思维聚焦在b+c的求解上.学生对运算表达式整体结构的认识,是明晰运算对象、探究运算思路、选择运算方法、设计运算程序、求得运算结果的前提.实际教学中教师应教会学生如何有效把握运算表达式的整体结构.
解法二:由a2=b2+c2-2bccosA及2a2=b2+c2,得a2=2a2-2bccosA,即a2=2bccosA.

又2a2=b2+c2=(b+c)2-2bc,所以(b+c)2=81,即b+c=9.
故△ABC的周长为a+b+c=14.

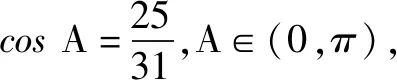


故△ABC的周长为14.

3 反思
“新”高考特别强调考查基础.要求学生深刻理解高中数学基本概念、基本思想方法以及数学问题的本质,重视数学知识的内在联系.教师应在高中数学教学中多设置一些富有探究性的数学教学活动,引导学生深化数学概念,内化数学方法;在拓展学生的数学知识视野上下功夫,着力提升学生应用数学知识的灵活性和创造性及关键能力.
“新”高考强化对思维方法的考查.体现在以引导学生深度理解数学概念和深刻认识数学思想方法为载体提升学生思维的灵活性,指向思维的灵活性以深化基础性的考查.要求学生具有较强的空间想象能力和分析问题的能力,能在抽象的情境中发现解决问题的关键.同时要求学生具备直观想象、灵活运算、猜想与证明等方面的能力.
“新”高考对中学数学教学的引领性告诉我们,数学教学的核心任务之一是要培养学生的思维能力,使学生在掌握数学基础知识的过程中,学会感知、观察、归纳、类比、想象、抽象、概括、推理、证明和反思等逻辑思考的基本方法.教师在教学中要引导学生重视数学知识的发生发展过程,多设置一些可以对学生进行思维训练的教学活动,通过多举措给学生提供思维训练的机会给学生,锻炼学生的思维能力,引导学生学会用数学的眼光观察世界、数学的思维思考世界、数学的语言表达世界.

