基于振动声调制信号协整分析的螺栓预紧状态识别

张俊树， 李 丹， 任伟新

(1. 合肥工业大学 土木与水利工程学院， 合肥 230009；2. 深圳大学 滨海城市韧性基础设施教育部重点实验室(筹)， 广东 深圳 518060)

螺栓作为连接件具有易于拆卸和承载能力强等优点，广泛应用于机械和土木工程等多个领域。螺栓的预紧力损失会降低结构的承载能力,直接影响结构的可靠性。为保证结构的完整性、安全性和功能性，需要对螺栓连接的预紧力状态进行检测和监测。

振动声调制(vibro-acoustic modulation,VAM)是一种基于接触非线性的超声检测方法，对结构中的缺陷十分敏感，可以有效地检测闭合微裂纹、复合材料分层和螺栓松动等接触性缺陷，且不需要复杂的设备来发生和采集信号，是近年来非线性超声检测技术研究的热点之一[1-4]。Klepka等[5]验证了VAM检测复合夹芯板冲击损伤的有效性； Zhao等[6]利用压电传感器(piezoelectric transducer, PZT)产生低频信号，通过快速傅里叶变换(fast Fourier transform, FFT)得到旁瓣幅值建立损伤指标，检测螺栓预紧力大小； Liu等[7]利用线性扫频信号替换高频谐波，结合同步解调和短时傅里叶变换(short-time Fourier transform, STFT)从输出信号中提取调制信息，用于检测混凝土裂纹。

上述研究中，结构的边界条件大致可分为两类：一类是放置在海绵垫上或用弹性绳悬挂，来模拟自由边界条件，这种方法适用于条件可控的实验室中；另一类是紧固在刚性基础上，以消除边界条件的影响。然而在实际应用中，结构的边界连接处也会发生损伤，例如螺栓连接边栓的影响。现有的方法无法很好地分辨调制信号是由结构还是边界产生。Polimeno等[8]发现完好的悬臂板在夹具松动的情况下，与存在裂纹悬臂板的VAM信号相同，会在频域中的高频信号两侧产生类似的旁瓣。因此，如何在复杂变化的边界条件影响下提取真实损伤的信息，对推动VAM在损伤检测和监测在实际中的应用至关重要。

在理想环境下，旁瓣幅值会随着损伤的增大而增大，且在损伤大小一定时，幅值随时间变化的序列是平稳的，损伤程度与幅值大小也是一一对应的。然而由于边界条件的不断变化，旁瓣幅值序列不再平稳，一一对应的关系被打破，导致VAM无法有效识别损伤。研究表明，各阶旁瓣幅值具有相同的变化趋势，如果能找到平稳的线性组合，就可以消除边界条件引起的幅值序列非平稳性。为消除长期监测过程中的结构边界条件影响，本文引入协整检验，以有效地表征螺栓的预紧力状态。

协整理论最初发展于计量经济学领域[9]，主要基于平稳性的概念。在研究过程中，若各变量之间具有协整关系，进行协整分析时，这些变量的线性组合会去除原始数据中的共同趋势，剩下等价于该过程长期动态平衡的残差。残差平稳表示结构处于正常或无损状态，任何偏离平稳的情况都可以表示被检测的对象或结构不在正常状态下运行[10-11]。基于此，协整检验近些年被国内外学者引入结构健康监测领域中，用于处理质量、温度等因素的影响。Dao等[12]对温度影响下的兰姆波信号进行小波变换，通过协整处理小波系数方差，分离出温度的影响；刁延松等[13]取结构加速度响应数据第一阶时间序列AR(autoregressive)模型系数为协整变量，去除了温度、质量对结构损伤识别的影响；Liang等[14]以固有频率作为协整变量，成功将协整改进的损伤识别方法应用到南京地铁口钢桁架桥和天津永和大桥；李秀娟等[15-16]利用协整分别消除了温度和动应力对压电阻抗法的影响。

本文利用协整分析在处理环境因素中的优点，提出了一种去除VAM中边界条件影响的螺栓预紧力识别方法。通过STFT提取VAM信号频域中的旁瓣幅值作为变量进行协整分析，分离边界条件的影响，通过协整残差识别连接板件的螺栓状态；再计算协整残差的均方根(root mean square，RMS)值构建预紧力指标PI(preloading index)，实现预紧力状态的识别。

1 螺栓状态VAM无损检测

无损检测过程中，向被测试件同时输入低频振动和高频信号，两种激励在螺栓松动处发生调制。低频振动用于推动螺栓与板件接触面的相对运动，使得松动处发生接触作用，其频率往往对应于一种固有频率时效果较好；高频信号则作为探测波收集信息，频率通常是任意选择的。当螺栓紧固时，结构可视为线性系统，接收到的信号为两激励的线性叠加，其频域仅有两列入射波对应的频率；当螺栓松动时，结构将在连接处变为非线性系统，由于两种激励在螺栓松动处的相互作用，高频信号会在连接处发生幅值和相位调制，进而产生了新的旁瓣调制谐波成分，即旁瓣信号，螺栓状态VAM的基本原理如图1所示。图1中：LF为低频频率；HF为高频频率；f为频率。左、右旁瓣在频域上的位置可用式(1)、式(2)描述

(a) 螺栓紧固状态的频谱

(b) 螺栓松动状态的频谱图1 VAM原理图Fig.1 Schematic diagram of VAM

FLSj=FHF-jFLF

(1)

FRSj=FHF+jFLF

(2)

式中：FHF为高频信号的频率；FLF为低频振动的频率；j为旁瓣的阶数。

由此可知，通过分析频谱中的高频旁瓣可判断螺栓是否松动。此外，能量[17]、时频[18]以及各种统计学方法[19]也被引入信号分析当中，用于改进VAM。然而利用VAM进行损伤检测依然面临一些实际问题：由于材料固有的非线性和边界条件等影响，经常能在没有损坏的试件中，观察到旁瓣成分，并且在低频振动幅度较大时，十分常见。

2 协整分析与检验

2.1 协整分析过程

协整分析是一种处理非平稳序列的有效手段。如果有两个或两个以上的变量序列是非平稳的，它们的线性组合可以产生新的平稳变量，则认为该变量之间具有协整关系，这种稳定线性组合称为协整向量。

对于非平稳变量y，经过d次差分后变成平稳序列，但若只进行d-1次差分，它仍然是非平稳的，那么变量y可称为d阶单整，记为y～I(d)；如果变量y是平稳的，则记为y～I(0)。对于一组同为d阶单整的非平稳变量YT=(y1,y2,…,yn)∈Rn，当且仅当它们满足式(3)时，称它们具有协整关系

α1y1+α2y2+…+αnyn=εn

(3)

式中：εn为平稳残差序列；(α1,α2,…,αn)为协整向量。

2.2 ADF检验

ADF(augmented dichey-fuller)检验是检验序列平稳性的一种经典方法，又称单位根检验。首先需要考虑一阶自回归模型

(4)

式中：β为确定的线性趋势(如趋势项或常数项)；p为滞后长度，可由信息准则确定，从而使残差序列为平稳序列；η，αi为系数；Δyn-i=yn-i-yn-i-1。

对式(4)中的yn作一阶差分可得

(5)

式中，γ=η-1。

序列yn是否平稳主要取决于γ值，如果γ=0，则回归过程有一个单位根，此时序列yn是非平稳的；当γ<0时，yn是平稳的。ADF检验通过估计假设γ=0的概率来判断序列的平稳性，利用γ的最小二乘估计和标准差估计的比值构造t统计量进行假设检验，将t统计量与临界值进行比较，若小于给定显著性水平的t统计量值，拒绝原假设，认为没有单位根，yn是平稳序列；否则接受原假设，认为yn是非平稳序列。

2.3 EG检验

EG(Engle-Granger)检验是Engle和Granger提出的基于回归残差的两步检验，可用于检验变量xt和yt之间是否存在协整关系，具体步骤如下。

步骤1如果变量xt和yt是两个一阶单整的序列，那么两者的回归方程同协整方程，可表示为

yt=a+bxt+τt

(6)

通过普通最小二乘估计得到残差序列为

(7)

式中：a为常数项；b为回归系数；τt为均值为0、方差为σ2的独立正态随机变量。

步骤2由于当xt和yt不存在协整关系时，它们的任何线性组合都是非平稳的，因此检验残差序列et是否平稳，即可判断xt和yt是否具有协整关系。

当et序列通过ADF检验判断为平稳时，xt和yt具有协整关系，a与b为协整向量的系数；反之不存在协整关系。

3 基于协整分析的螺栓预紧状态识别方法

国内外学者已经提出多种损伤指标和信号处理方法[20-22]改进VAM，但实验验证的环境十分理想，经常忽略边界条件等因素的影响。

以上研究也表明，损伤引起的各阶旁瓣幅值具有共同趋势，即随着损伤的增大而增大。参考计量经济学中协整的处理方法，同时排除共振峰偏移的影响[23]，选取调制信号低频侧一阶和二阶旁瓣幅值作为协整变量。协整分析表明，当螺栓紧固时协整残差是平稳的，当螺栓松动时板件的接触面和刚度等会发生变化，幅值序列不再满足之前的协整关系，残差变为非平稳，为螺栓状态识别提供了可能。

假设基准样本的协整残差服从正态分布，通过设置残差序列的上下限识别螺栓状态，一旦残差超出控制线，则可以判断螺栓发生松动。基于协整分析改进的VAM方法的螺栓预紧状态识别流程，如图2所示。

图2 预紧力识别流程Fig.2 Flowchart of bolt looseness identification

为判断板间预紧力状态，本文提出利用旁瓣幅值作为变量，进行协整检验得到残差，将残差序列的RMS值作为预紧力指标IP

(8)

式中：(x1,x2…xn)为协整残差序列；n为残差序列的样本点数。IP与螺栓预紧力损失呈线性关系，可建立基于协整残差的板间预紧力损失评估模型，更准确地判断螺栓预紧力状态。

4 实验及结果分析

4.1 实验过程

实验选取尺寸为120 mm×35 mm×5 mm，材质为Q235的两块钢板作为实验试件。两钢板通过一强度级为8.8的M8螺栓连接，该螺栓称为板间螺栓，预紧力大小称为板间预紧力；边界处用相同的螺栓固定在刚性基础上，该螺栓称为固定螺栓，预紧力大小称为边界固定力，如图3所示。实验通过改变边界固定力大小来模拟边界条件变化，计算IP识别板间预紧力状态。

图3 实验配置示意图Fig.3 Schematic of the specimen configurations

实验采用PZT作为发生高频信号和采集信号的传感器，分别粘贴在板间螺栓悬臂侧和边界侧400 mm中心处，称为PZT1和PZT2。针对低频激励，利用力锤敲击试件，采集振动信号，找到一阶固有频率作为低频激励的频率，低频振动由激振器直接作用在钢板的悬臂末端，频率和激振力大小分别为1 280 Hz和20 N；高频信号由系统软件LabVIEW编程，通过NI数据采集仪传输至功率放大器提高电压后，由PZT1作用到钢板上，其频率是经过调试后，选择的效果较好的频率，本文高频激励的频率和放大后的电压分别16 560 Hz和700 V。由PZT2采集VAM信号，NI数据采集仪记录。

根据JGJ 82—2011《钢结构高强度螺栓连接技术规程》，计算得到强度级为8.8的M8螺栓的施工预紧力为23.144～31.560 N·m，为保证螺栓拧紧，将35N·m设为螺栓紧固时的预紧力。首先，利用扭力扳手将板间螺栓拧至紧固状态，以1 N·m为步长，从35N·m到1 N·m线性减小边界固定力，再从1 N·m到35 N·m线性增加边界固定力，每隔一个步长采集一次数据，作为螺栓紧固状态下的基准信号；再设置板间预紧力以5 N·m为步长，从30 N·m到5 N·m线性减小，在这6种板间预紧力的状态下，均进行一次上述边界固定力线性减小的过程，采集得到6组损伤信号。整个实验过程总共采集到7组数据，基准信号组70个信号，6组损伤信号各35个信号，合计280个信号。实验装置如图4所示。

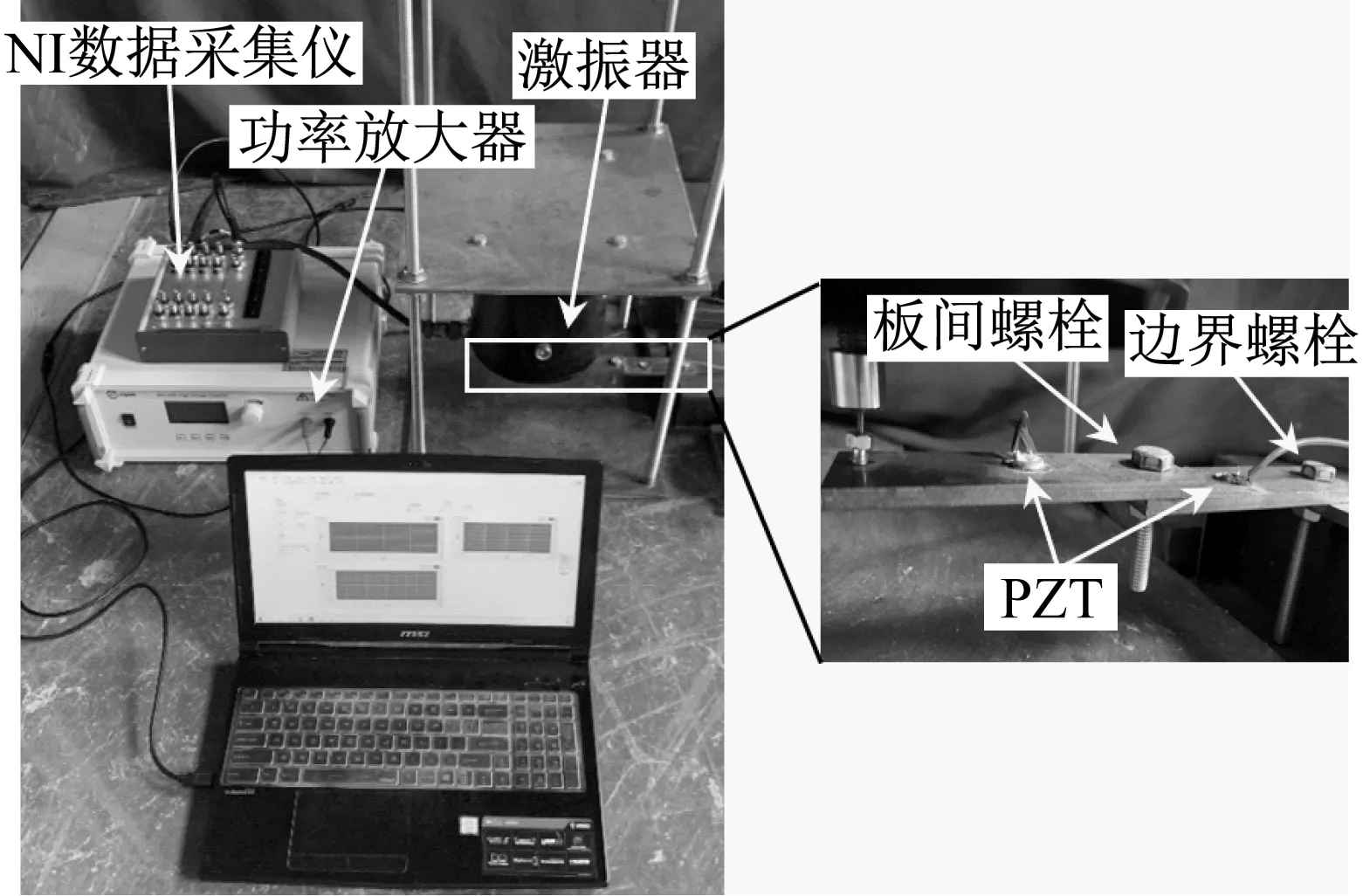
图4 实验装置Fig.4 Experimental setups

4.2 结果与讨论

4.2.1 边界固定力对旁瓣幅值的影响

实验证明当边界螺栓发生松动，即使板间螺栓处于紧固状态，采集信号频谱中也能观察到旁瓣成分。边界固定力20 N·m，板间预紧力35 N·m状态下的FFT频谱图，如图5所示。图5中已将低频振动部分滤除。此时板间螺栓紧固，边界螺栓松动，频谱中高频信号两侧出现明显的旁瓣，容易造成螺栓预紧力状态的误判。从图5中还可以看出，高频侧与低频侧相同，各阶旁瓣幅值依次递减。

图5 高频信号两侧旁瓣信号傅里叶频谱图Fig.5 Fast Fourier transform of the sideband signals nearby the high-frequency signal

传统的信号处理方法通常是利用FFT提取旁瓣幅值，建立预紧力指标ID(damage index)

ID=(ALB+ARB)/2

(9)

式中：ALB为低频侧一阶旁瓣幅值；ARB为高频侧一阶旁瓣幅值。结果如图6和图7所示。

图6 板间预紧力为20 N·m和35 N·m的IDFig.6 ID of the bolt preloading at 20 N·m and 35 N·m

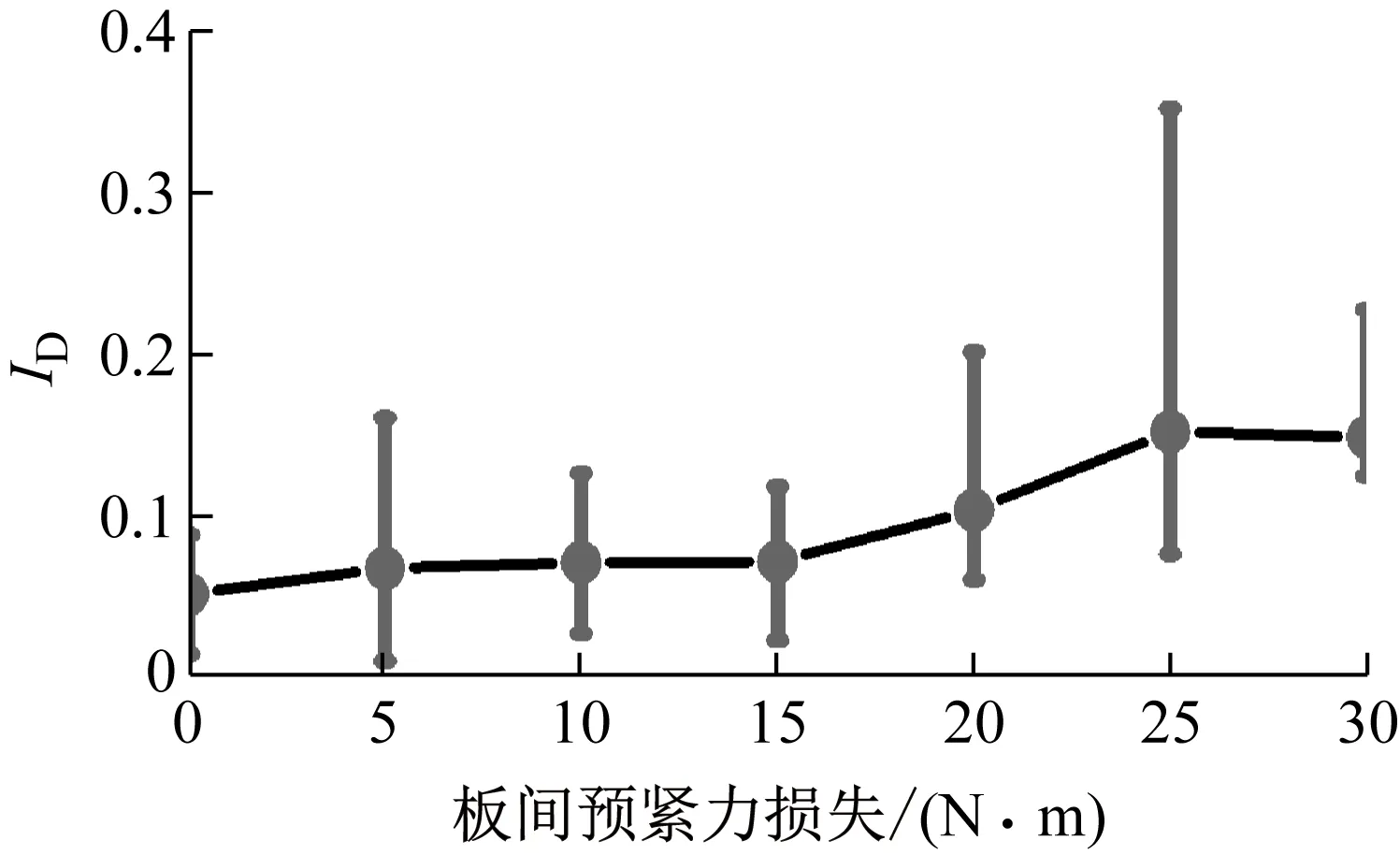
图7 不同板间预紧力的ID误差线Fig.7 ID error bars of the bolt preloading

图6给出板间螺栓在两种状态下，ID在不同边界固定力下的值。观察发现，不论板间预紧力大小是20 N·m还是35 N·m，边界固定力的大小都会影响ID，使其在一定范围内浮动，很难从中提取稳定的指标。

图7是不同板间螺栓状态下的ID误差线，表示不同板间预紧力下，ID的浮动范围，图7中圆点为该板间预紧力下ID的均值。可以看出，ID受边界固定力的影响会在一定范围内浮动，且不同板间预紧力状态下的浮动范围之间存在大量交叉，无法有效判断板间螺栓状态。因此，在传统预紧力指标下，边界固定力会对板间预紧力的识别造成重大影响，甚至淹没真实的结果。

4.2.2 构建旁瓣幅值序列

低频振动由激振器产生，实际振幅远大于高频信号，为防止旁瓣过小难以分辨，首先滤除所有采集信号的低频部分。为了更好地反映信号的时频特性，采用STFT，得到的时频图如图8所示。再归一化并提取各阶旁瓣幅值得到7组数据，取每组数据的低频侧前两阶旁瓣幅值组成两个序列。由基准信号组提取的两个旁瓣幅值序列，如图9所示。由图9可知，两个序列具有相同的变化趋势。

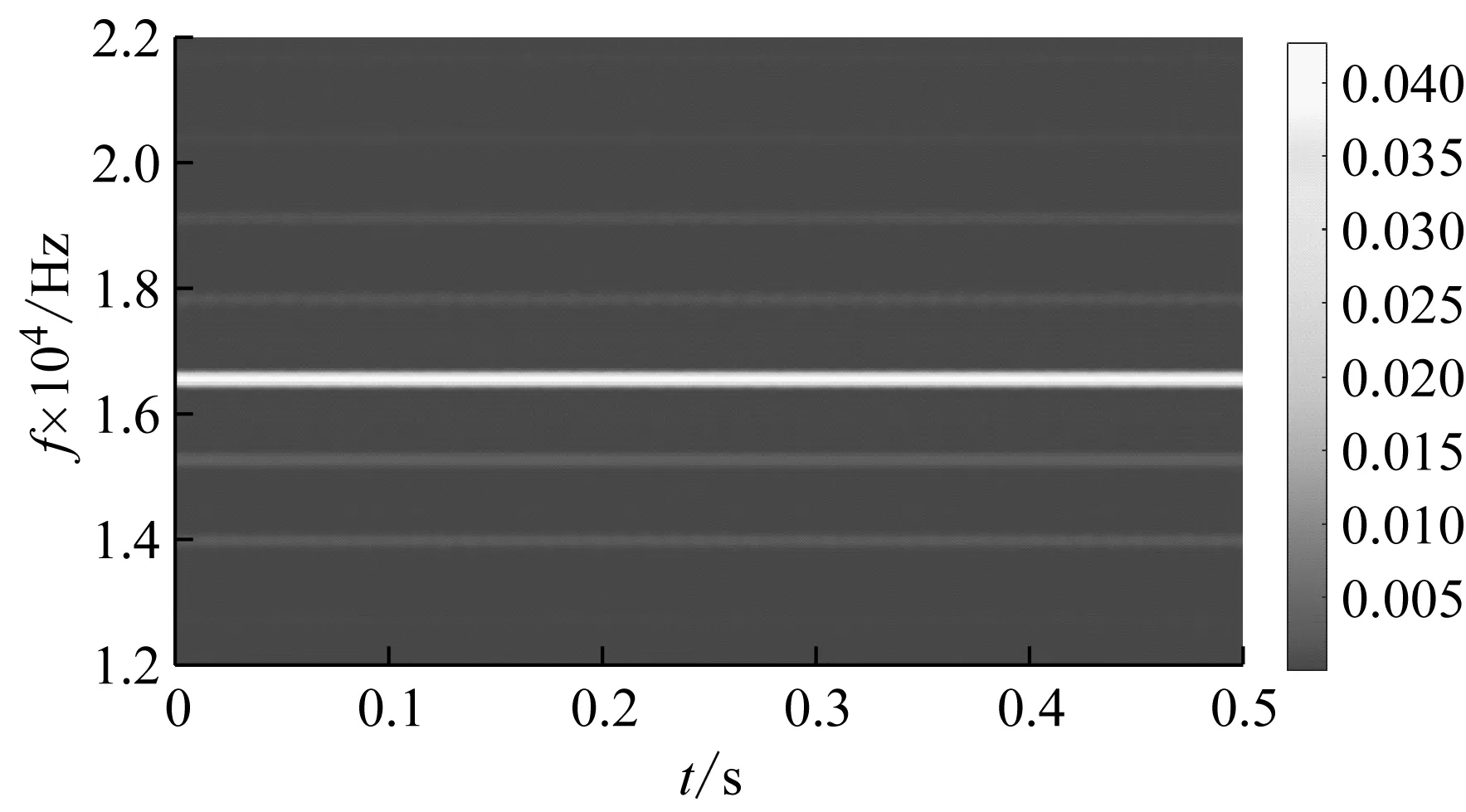
图8 VAM采集信号时频图Fig.8 Time-frequency spectra of VAM signal

图9 板间螺栓紧固时的幅值序列Fig.9 The sideband series of the tightening bolt between plates

4.2.3 协整分析

根据2.2节内容，对上述两个序列进行ADF检验，计算t统计量，并行显著性检验。对比5%显著性水平的临界值-1.941，可判断两序列是非平稳的；再对序列作一阶差分后，执行上述相同步骤，可认为两个一阶差分序列是平稳的。结果显示两个序列同为一阶单整，满足协整检验的条件，如表1所示。

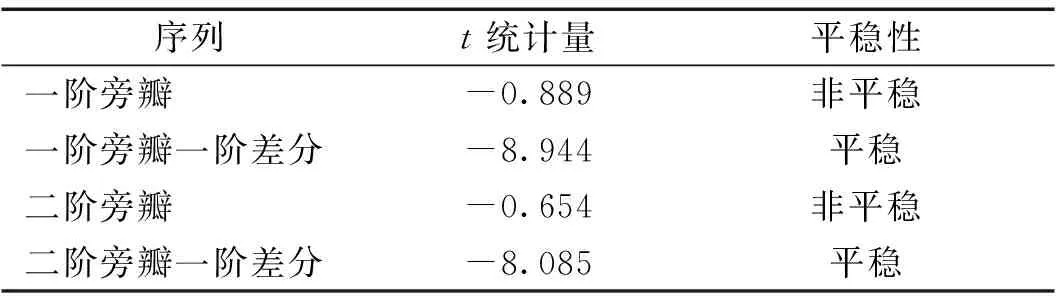
表1 旁瓣幅值序列及其一阶差分的ADF检验结果Tab.1 ADF test results of sideband series and its first difference

对上述两序列进行EG检验，得到协整方程为

et=A1-1.171 016A2-0.257 21

(10)

式中：et为协整残差；A1为一阶幅值序列；A2为二阶幅值序列。再对协整残差作ADF检验，得到残差的t统计量为-6.652，小于5%显著性水平对应的临界值，可以判断两序列之间存在协整关系。将余下6组幅值序列代入协整方程中，对比残差的变化，结果如图10所示。

图10 不同板间预紧力的协整残差Fig.10 Cointgration residual of different preload between plates

图10中，纵向虚线表示不同板间预紧力工况的分界线。当板间预紧力小于35 N·m时，由于预紧力损失较小，板间螺栓轻微松动，两幅值序列之间的协整关系改变，原本的协整关系不再适用，残差开始向上偏移，部分超出控制线；当板间预紧力小于25 N·m时，板间螺栓发生明显松动，残差大量超出控制线范围；随着预紧力损失的增大，协整残差的偏离距离也随之增大，说明协整残差不仅可以去除边界条件的影响，而且可用于判断板间螺栓预紧力状态。将各个工况下的残差代入式(9)，计算得到IP，构建基于协整残差的板间预紧力损失评估模型

IP=0.006 34×LP-0.006 81

(11)

式中，LP为板间预紧力损失。随着预紧力损失的增大，IP值也随之增大，能够有效识别预紧力状态，但在板间预紧力损失为10 N·m时，可能由于激振器过载导致误差较大，如图11所示。

图11 基于协整残差的板间预紧力损失评估模型Fig.11 Evaluation model of the bolt preloading loss based on cointegration residuals

5 结 论

螺栓连接结构的边界条件会对螺栓预紧力的识别造成影响，导致螺栓松动的误判。本文基于协整检验处理旁瓣信号幅值，消除边界条件的影响，构建预紧力状态评估模型。通过螺栓连接悬臂钢板在边界固定力变化工况下的VAM实验，发现边界固定力变化会使传统的预紧力指标上下浮动，造成不同板间螺栓工况的预紧力指标数值大量交叉。但频谱中，高频信号两侧旁瓣幅值依次递减，且具有相同的变化趋势。

本文考虑边界条件影响，选取了非平稳的一阶、二阶旁瓣幅值序列为研究对象，进行协整检验，通过协整向量得到平稳的协整残差。结果表明，损伤发生后，序列不再满足之前的协整关系，导致协整残差偏移，验证了协整处理边界条件方法的有效性。基于所求的协整残差，建立了具有鲁棒性的预紧力指标IP，得到预紧力状态评估模型，可在结构长期监测中消除边界条件的影响，更加准确地识别螺栓预紧状态。目前本文的方法仅在单螺栓结构中得到验证，针对复杂螺栓连接结构，需首先判断松动螺栓位置，进而研究其预紧力大小，在后续工作中，将结合VAM信号的信息熵对此开展进一步的研究。