小肠环境下自推进胶囊内窥镜的非线性动力学行为研究
朱佳鹏, 廖茂林, 朱志强, 曾子衿, 李 智
(北京科技大学 机械工程学院, 北京 100083)
随着肠胃病患者基数不断增加,消化道的医疗检测需求量大幅增加,然而传统的内窥镜检查的管线探头结构,在检测过程中易对患者造成强烈的不适感,并存在对病变区域造成二次伤害的安全隐患。为有效解决此类问题,无线式胶囊内窥镜逐渐引起关注,目前可作临床使用的无线式胶囊内窥镜主要分为磁控式与被动式。其中,磁控式无线内窥镜胶囊依靠大型的磁控设备与胶囊表面的磁控衣作用,控制胶囊在消化道当中的运动,并利用胶囊自身的图像采集功能完成检测[1],但其费用昂贵,操作复杂。而被动式胶囊内窥镜虽然成本较低,操作简单,但由于胶囊在消化道内的移动仅依靠肠胃的蠕动,无法主动靠近或远离病变区域[2],给检测带来诸多不便的同时还存在无法排出体外的隐患。
为更好地解决无线式胶囊内窥镜的驱动问题,激振冲击方式被引入对胶囊进行结构改造。激振驱动胶囊系统由Liu等[3-4]在研究偏远地区管道检测问题时被提出,随后被考虑用于消化道的无线检测。其核心思想是在胶囊内部设置一个激振冲击结构,通过内部激振体与胶囊外壳的周期性冲击碰撞驱动胶囊以一定速度进行自推进移动。在此基础上,对具有单边和双边约束结构的自推进胶囊进行了对比分析[5-6],发现单边约束结构更容易实现胶囊的高速移动,而双边约束结构则在实现胶囊的双向移动方面更具优势。
然而,胶囊内窥镜的主要运行环境为消化道,其小肠部分在变形时具有指数增强的强非线性应力-应变响应[7]。因此,胶囊内窥镜在通过狭隘的小肠时,除了库伦摩擦阻力,还会受到其他多种肠道阻力的影响。针对此类问题,Ciarletta等[8]利用超弹性理论对肠壁进行了分层分析,并提出了五应力超弹性模型,该模型对肠道的力学模型搭建具有重要意义。随后,Kim 等[9-10]基于Ciarletta 模型建立了胶囊在小肠内运动的摩擦阻力模型,并利用该模型开展试验,测量了不同尺寸的胶囊通过猪小肠内部与表面时的摩擦阻力,最终得到其范围在[10 mN,50 mN]。谭人嘉等[11]利用Ciarletta 模型,分别建立了胶囊机器人头部压力、中段摩擦力和头部摩擦力的阻力模型,并通过试验发现胶囊半径与肠道半径之比和肠道摩擦因数的增大都会导致胶囊前进阻力增大。Tian等[12]则从胶囊的安全性出发,用不同形状与速度的胶囊依次通过平坦、塌陷、收缩和弯曲4种不同的小肠结构,发现当速度处于[4 mm/s,10 mm/s],胶囊柱段的半径等于胶囊末端的长度时,对肠道的损伤最小。此外,也有学者[13]从胶囊的移动速度出发,得到胶囊受到的摩擦阻力范围在 [10 mN,250 mN];而针对小肠收缩率[14]进行试验得到了胶囊受到的收缩压力峰值约为0.24 kPa。
因此,目前的问题主要集中在如何将建立好的肠道阻力模型与自推进胶囊内窥镜的动力学模型耦合,从而更好的对胶囊在小肠中的运动进行分析。为此,Yan等[15]建立了胶囊在小肠中运动的动力学模型,并以低能耗与高速度作为参考指标制定了胶囊的最优参数,这也为本文阻力模型的搭建提供了参考思路。从肠道环境的不稳定性出发,Liao等[16]利用组合优化算法,得到了自推进胶囊在摩擦因数变化的肠腔内运动时,5种不同运动的控制参数,包括前进(快慢)、后退(快慢)和悬停,并在此基础上,Zhu等[17]对自推进胶囊在肠道中运动的能耗、速度与外部驱动力三者进行了多目标优化。此外,Guo等[18-19]利用试验对3种不同小肠环境下自推进胶囊的运动进行优化分析,得到胶囊在肠道中最大前进速度为8.49 mm/s,最大的反向运动速度为-4.9 mm/s。
虽然国内外学者们已经开展了大量相关研究,但是大多并未考虑肠道的蠕动以及肠道内流体环境对胶囊运动的影响。鉴于此,本文将搭建小肠-胶囊耦合模型,在小肠阻力分析的基础上充分考虑小肠的能动性,分析肠道蠕动下自推进胶囊在通过狭窄小肠段时的动力学特性,讨论胶囊的激振参数和结构参数对自推进胶囊的非线性动力学行为演化规律的影响,以及分析流体环境对胶囊运动的影响。从而为实现胶囊在小肠中的最优移动,并为自推进胶囊内窥镜的研发方案提供支撑。
1 小肠-胶囊动力学模型建立
1.1 自推进胶囊的动力学模型
为实现在不需要增加外部大型配套设备的情况下,胶囊在消化道中具有可控的移动能力,考虑在胶囊内部设置磁致伸缩式的激振冲击结构来赋予胶囊自推进能力。自推激振胶囊的物理模型如图1所示,质量分别为mc,mm的胶囊外部壳体和内部激振体通过一个Kelvin-Voigt(k1-c)模型相连,且胶囊内部右侧设置代表胶囊壳体刚度的弹簧k2。激振体在简谐激励Fa作用下发生振动时,会产生与外部壳体的相对位移Xm-Xc,当相对位移大于两者间的间隙e1时,激振体会与弹簧k2发生碰撞,这使得胶囊具有了接触非线性特征。鉴于此,根据胶囊内部激振体与弹簧k2是否发生碰撞,可以将胶囊分成以下两个移动阶段。
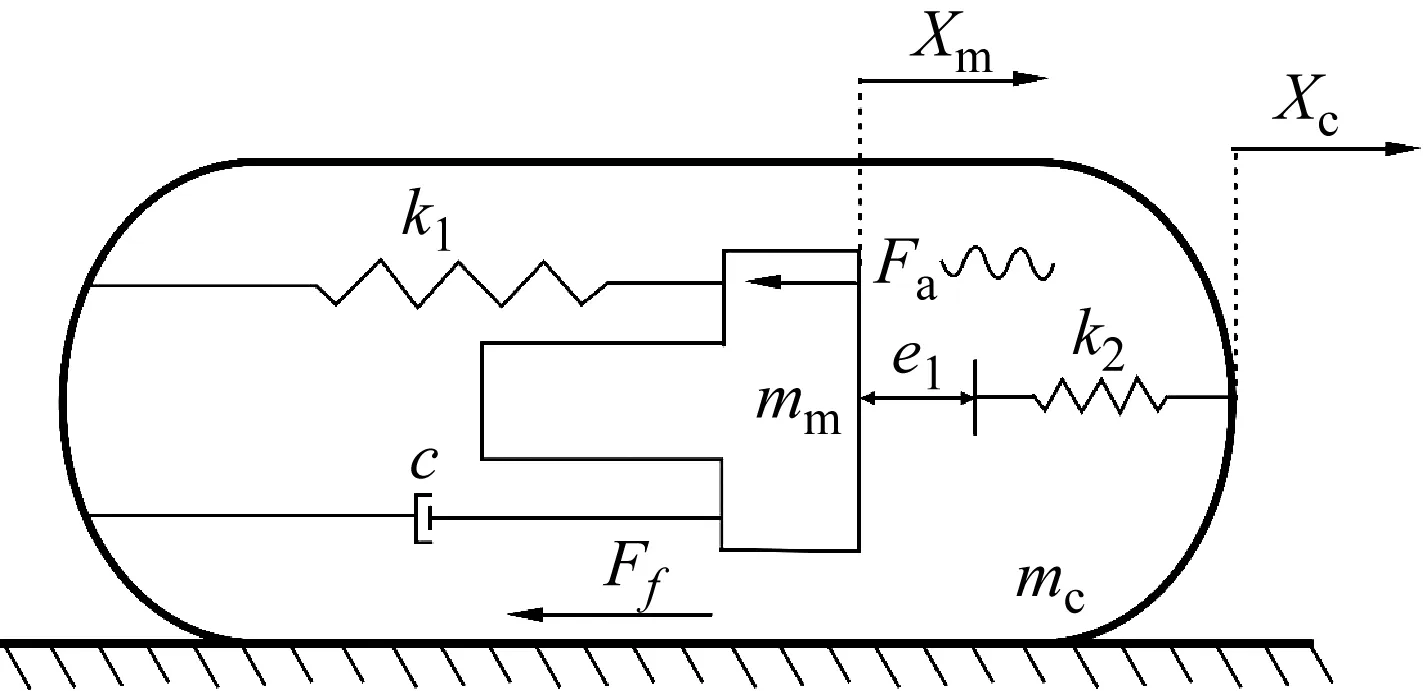
图1 自推进胶囊基础物理模型Fig.1 Physical model of self-propelled capsule
(1) 当激振体与胶囊发生碰撞:Xm-Xc≥e1
此时,激振体mm的振动方程如式(1)所示
(1)
式中:Pd为激振振幅;f为激振频率;Fc为胶囊外壳受到的内部作用力,当Fc大于外界阻力Ff时,胶囊整体开始运动,具体表达式为
(2)
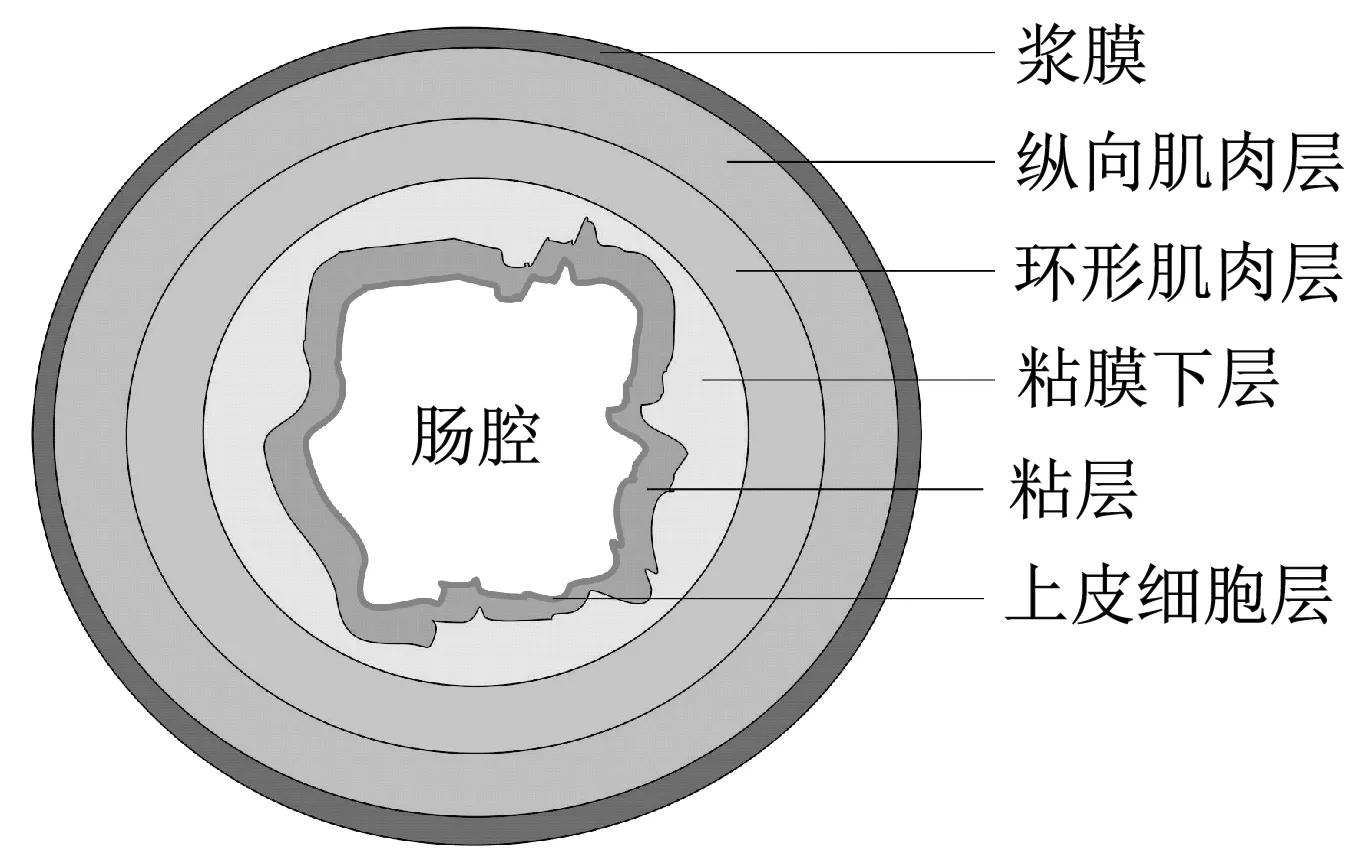
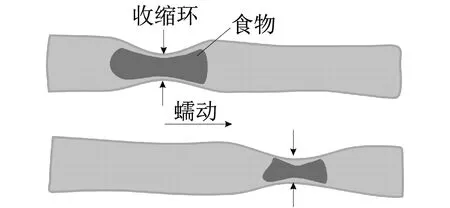
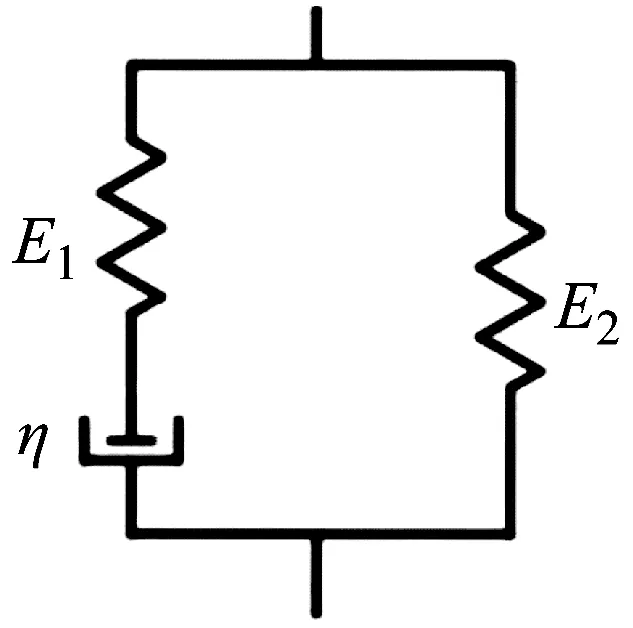
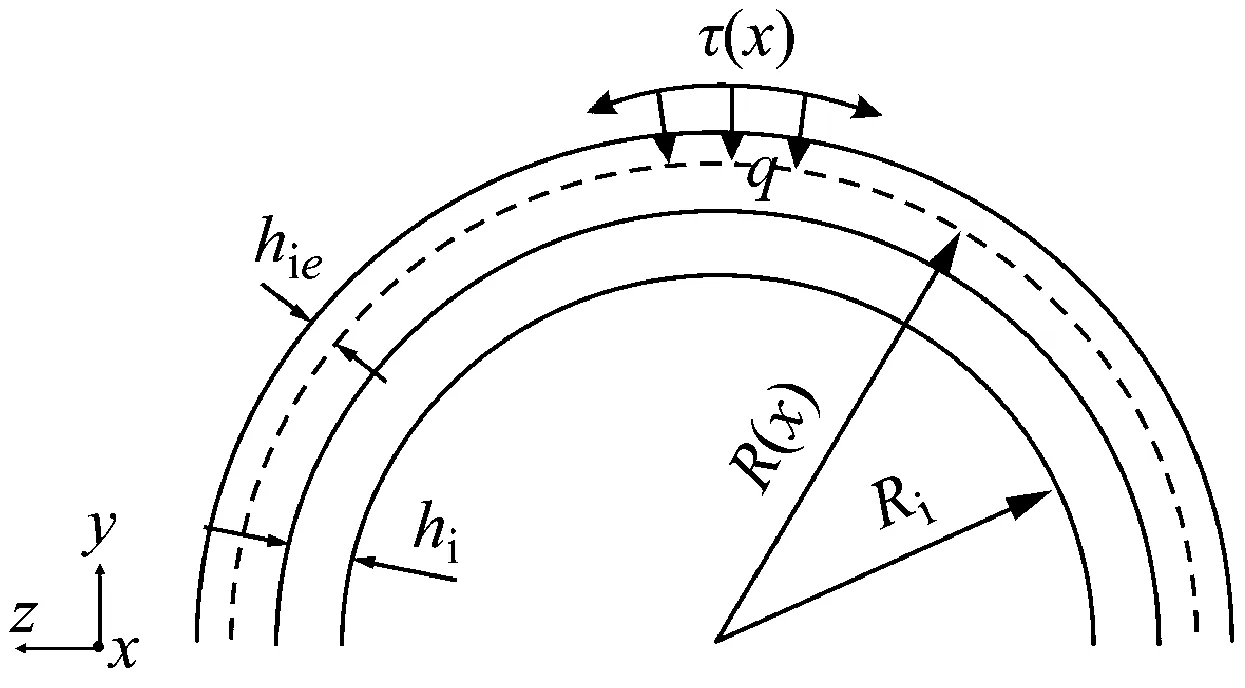
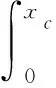
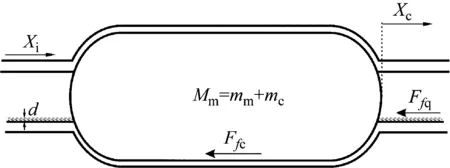
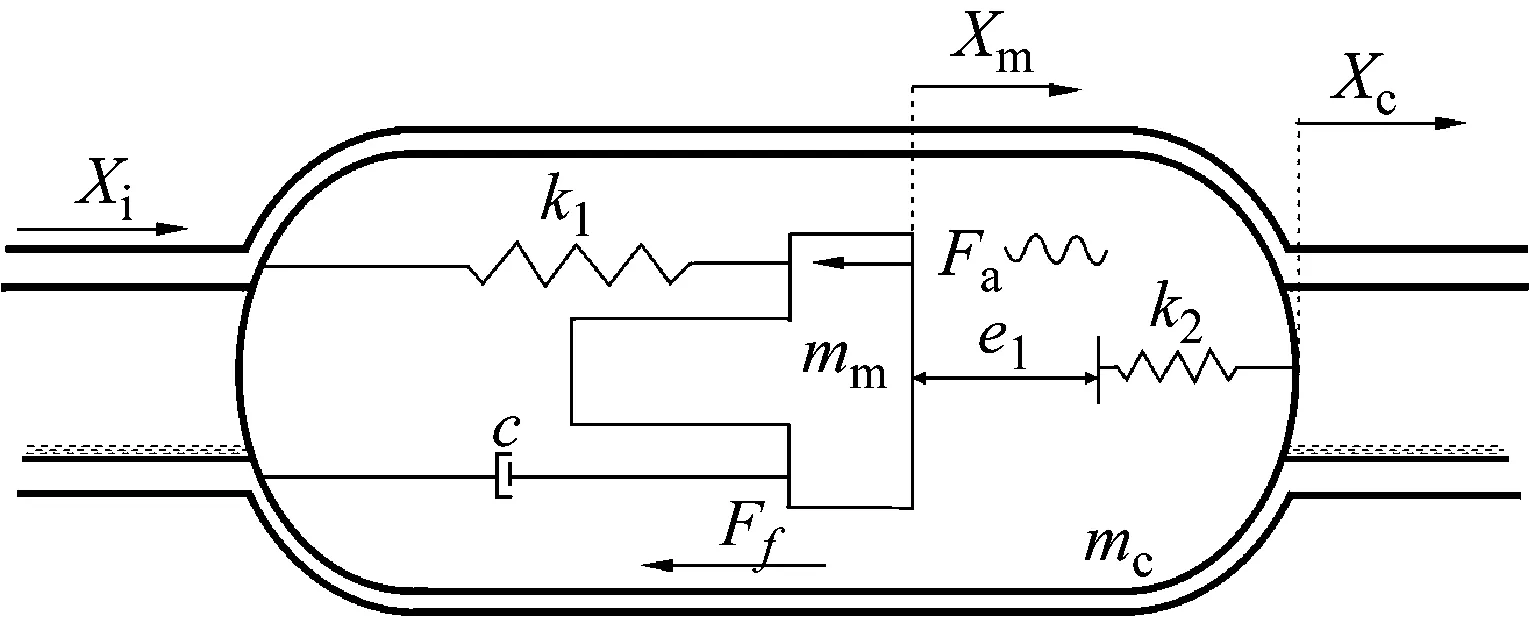
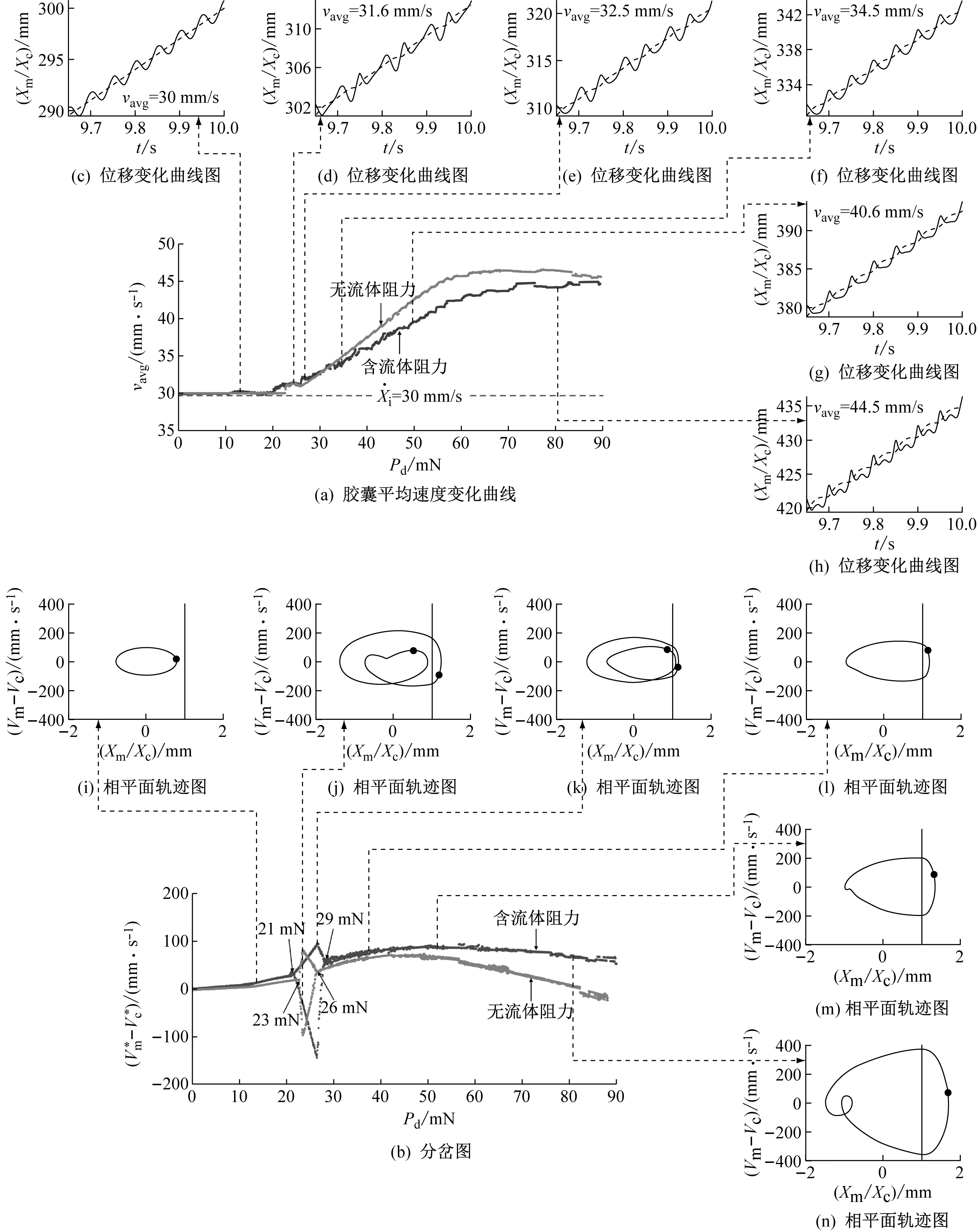
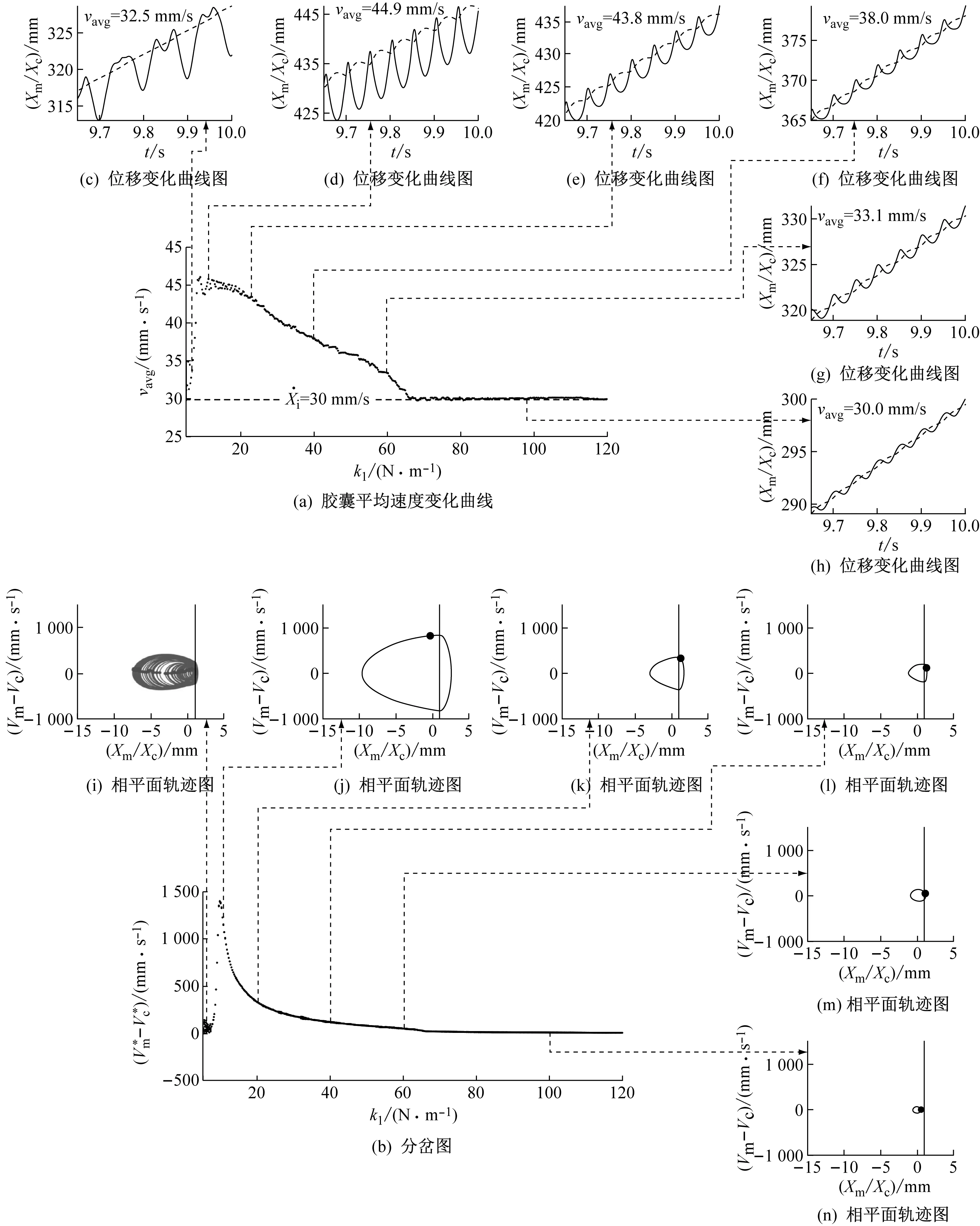
(2) 当激振体与胶囊未发生碰撞时:Xm-Xc 激振体的振动方程可用式(3)表示为 (3) 当胶囊外壳受到的内部作用力Fc大于外界阻力Ff时,胶囊整体开始运动,具体表达式为 (4) 在此基础上,进一步引入Heaviside判定函数,对胶囊系统的各个移动阶段的动力学方程进行整合 (5) 综上,自推进胶囊的动力学模型可以表示为 (6) 其中 胶囊在吞咽后,会经过人体的食道、胃、小肠和结肠,最后经肛门排出;其中小肠作为主要的消化道器官,整体长度达4~6 m,其结构最为复杂,对胶囊移动限制也最大。因此考虑对狭窄的小肠进行建模,以对自推进胶囊在其内部的移动规律进行分析。 小肠的横截面如图2(a)所示,其结构包括了浆膜、纵向肌肉层、环形肌肉层、粘膜层(含粘膜下层与粘膜)与上皮细胞层。从其功能方面来看,小肠依靠收缩环的不断推进形成蠕动波完成对食物的运输,过程中肌肉层与粘膜层对小肠的运动进行协调,如图2(b)所示。由此可知,当胶囊在肠腔内运动时,会受到小肠结构的应变应力与蠕动的作用,为此需要建立小肠的应力应变模型并且确定其蠕动速度,从而实现对小肠的建模分析。 (a) 小肠横截面 (b) 小肠蠕动示意图图2 小肠结构图Fig.2 Structure of small intestine 1.2.1 应力应变模型 小肠结构同时具备黏弹性与弹性两种力学特征,其中粘膜层和上皮层是黏弹性的,而弹性主要来自肌肉层。但相比于弹性,黏弹性在描述小肠组织随时间变化的力学特性方面更具优势,因而通常被用来代表小肠的特性。 因此,选择小肠的黏弹性作为研究对象,通过引进三元麦克斯韦模型对小肠的黏弹性进行建模,如图3所示,并得到小肠的应力应变关系表达式为 图3 三元麦克斯韦模型Fig.3 The ternary Maxwell model (7) 式中:ε(t)为小肠的应变;E1,E2为模型中涉及的两项杨氏模量;η为阻尼黏性系数;t为时间。 1.2.2 小肠蠕动速度 图4 收缩环速度变化曲线Fig.4 Speed variation of shrink ring 基于自推进胶囊的动力学模型与小肠模型,进一步分析两者耦合作用下,胶囊在通过狭窄的小肠段时受到的外界阻力Ff,分别从包裹阻力,流体阻力与摩擦阻力3个方面构建小肠-胶囊阻力模型。 1.3.1 包裹阻力模型 考虑到胶囊在通过小肠时会持续受到收缩环的作用,且胶囊直径与小肠肠径接近,因此胶囊在小肠内运动时,全程基本处于整体包裹型的内壁环境中,如图5所示。针对小肠段的包裹阻力,建立了分段力学模型,将胶囊受到的肠道阻力分解为头、中、尾3个区域,其中头部受到来自小肠水平方向挤压力形成的阻力Fhp,与垂直方向挤压力形成的摩擦阻力Fhf。同理,尾部受到水平挤压阻力Ftp,摩擦阻力Ftf,而胶囊的中部仅受到小肠的垂直方向挤压力产生的摩擦阻力Fmf,如图5所示。 图5 包裹式内壁环境下胶囊整体受力Fig.5 Force analysis of capsule in wrapped inner wall (a) (b)图6 胶囊头部受力分析Fig.6 Force analysis of capsule head (8) 并通过引入式(7)可以得到相应的小肠应力为 (9) 基于小肠应力的分析,进一步推算胶囊受到的挤压力,如图6所示,首先分析小肠与胶囊挤压后的变化,厚度由初始值hi变为hie,由式(10)表示为 (10) 结合式(9)与式(10),可以得到胶囊头部区域受到的压强表达式 (11) 引入dS(x)表示为某一位置的环向受力面积,从而计算出胶囊头部任意区域受到的挤压力dp(x),表达式为 dp(x)=q(x)dS(x)=q(x)2πR(x)· (12) 式中,R′(x)为R(x)的导数。 得到作用于胶囊壁面的挤压力后,将其分解为水平与垂直方向的力,开始讨论胶囊受到的外界阻力,其中水平方向的挤压阻力Fhp为 (13) 式中,cosφ(x)=(xc-x)/Rc,垂直方向挤压力引起的水平摩擦阻力Fhf由式(14)表示 (14) 式中,μ为小肠环境的摩擦因数。 同理可得,胶囊尾部的压力导致的水平挤压阻力为 (15) 此时的cosφ(x)=(xc+L-x)/Rc<0,L为胶囊中部柱段长度,x∈[xc+L,2xc+L],为胶囊尾部受到的水平挤压阻力与头部相反,胶囊尾部垂直方向的压力引起的Ftf水平摩擦阻力为 (16) 胶囊中部柱段受到的压力与x方向垂直,因此只产生水平方向的摩擦阻力,其表达式为 (17) 综合式(13)~式(17),其中水平方向的头部挤压阻力Fhp与尾部挤压阻力Ftp相互作用下结果为零,最终可以得到包裹阻力Ffi Ffi=Ftf+Fmf (18) 1.3.2 流体阻力模型 除去小肠包裹作用引起的阻力,胶囊自身的移动速度与小肠的蠕动速度会形成一定的相对速度,加上肠腔表层流体环境的影响,如图7所示,胶囊在小肠中移动时全程会受到流体阻力Ffq作用,具体表达式[21]为 图7 流体阻力与库伦摩擦阻力Fig.7 Fluid resistance and Coulomb friction resistance (19) 式中,d为流体厚度。 1.3.3 库伦摩擦阻力模型 此外胶囊在小肠环境中还受到自身重力带来的库伦摩擦阻力Ffc,如图7所示,表达式为 Ffc=Mmμg (20) 式中:g为重力加速度;Mm为胶囊系统的总质量。 最终通过以上3个模型分析,可得到胶囊在小肠中运动时受到的外界阻力Ff可以表示为 Ff=Ffi+Ffq+Ffc (21) 图8 小肠-胶囊物理模型Fig.8 Small intestine-capsule physical model 可见,相比于初始的胶囊模型,小肠-胶囊模型不仅要考虑碰撞导致的接触非线性特征,还需要对小肠蠕动速度与胶囊自推进速度之间的相对速度变化引起的阻力Ff方向进行判定。为此,需要在激振胶囊模型的基础上引入两个新的Heaviside函数,以考虑小肠与胶囊相对速度的影响 (22) 结合肠壁包裹环境下对应的Ff表达式(21),最终建立小肠-胶囊的耦合动力学模型 (23) 此外,为更好地了解自推进胶囊在小肠环境下移动速度变化规律,计算胶囊在单位时间内的平均速度 (24) 式中:N为周期数;T=1/f为单个激励周期。 利用建立的小肠-胶囊耦合动力学模型,进一步分析自推进胶囊在小肠环境中的非线性动力学行为特性。根据前人[22]对小肠结构的试验研究,首先确定了小肠参数,如表1所示。并从胶囊的应用要求出发,初步确定了胶囊的结构参数与激振参数,激振参数主要为式(1)中激振力Fa中的频率、振幅,如表2所示。选择胶囊的激振参数(频率、振幅)与部分结构参数(激振体的质量与刚度)作为研究对象,通过大范围调节各项参数,得到胶囊在小肠中运动的非线性动力学行为演化规律。具体而言,对胶囊进行分岔分析、相平面分析,以及速度变化对比,并通过确定自推进胶囊最优速度出现时的系统动态响应,为制定合理的激振控制方案与胶囊结构设计提供支持。 表1 小肠参数表Tab.1 Parameters of small intestine 表2 胶囊参数表Tab.2 Parameters of capsule 采用四阶龙格库塔算法对建立的小肠-胶囊耦合动力学模型进行数值求解,计算200个激励周期,并取最后10个周期作为参考,以确保自推进胶囊处于稳态响应状态。 为进一步分析流体阻力对胶囊运动带来的影响,分别在图9(a)、图9(b)中分别比较了有无流体阻力胶囊的平均速度曲线与分岔图,如图10所示。无流体阻力时胶囊的速度得到小幅提升,在振幅为60 mN时,两者速度差最大,且胶囊系统的分岔区间由之前[21 mN,29 mN]缩减至[23 mN,26 mN]。 图9 关于振幅Pd的动力学分析(图9(c)~图9(h)中虚线表示胶囊外壳,实线表示激振体;图9(i)~图9(n)中直线为撞击面位置,圆点为庞加莱截面截取的点)Fig.9 Dynamic analysis of amplitude 接着,以频率f作为变量,参数区间为[0,50 Hz],参数间隔取0.05 Hz,得到胶囊的平均速度变化曲线图图10(a)与分岔图图10(b),与Pd不同,在f的变化区间内,胶囊系统始终保持单周期运动,其中,当频率达到10 Hz时,激振体开始与壳体碰撞,见图10(i),此时胶囊的速度为29.9 mm/s,与小肠蠕动速度基本保持一致,见图10(a)。当频率增大到15 Hz时,见10(j),单个激励周期下激振体将与壳体发生两次碰撞,值得注意的是,此时胶囊平均速度vavg下降到21.3 mm/s,见图10(d),相对于小肠蠕动速度30 mm/s,胶囊在往反方向移动,这表明选择合理的激振频率可以控制胶囊的双向移动。继续增大频率至17 Hz时,见图10(k),激励周期内的碰撞次数重新回到一次,且由图10(c)可知,此时胶囊的平均速度达到最大为39.3 mm/s。当频率处于25~35 Hz时,以30 Hz,35 Hz为例,vavg基本稳定,速度保持在36 mm/s附近,且碰撞次数保持为一次,见图10(f)、图10(g)、图10(l)、图10(m)。一直到f=36 Hz时,见图10(n),激振体与壳体之间碰撞消失,胶囊静止仅随肠道蠕动前进,速度为30 mm/s,见图10(h);由此可知,当激励频率过高时,反而无法推动胶囊高效移动。 为保证自推进胶囊在小肠内的高效稳定移动,不仅要对激振参数进行调节,还需合理设计胶囊的结构参数;因此,本文以胶囊激振体的质量mm与刚度k1作为研究对象,分析结构参数对自推进胶囊的动力学行为演化规律的影响。 首先,分析胶囊激振体的质量mm,其参数区间设为[1 g,10 g],参数间隔为0.05 g,结果如图11所示。观察发现,m1在区间内变化时,激振胶囊始终保持单周期运动,见图11(b)。初始阶段,当mm=1.1 g时,胶囊速度为22.82 mm/s,相对于小肠往后运动,系统单个激励周期内发生了两次碰撞,见图11(c)、图11(i)。当mm=1.4 g时,由图11(d)、图11(j)可知,系统变为单周期单碰撞状态,胶囊平均速度速度达到38.29 mm/s,移动方向转为相对小肠向前运动。持续增大mm至7 g,vavg呈现先减小再增大至稳定的变化趋势,过程中整体变化幅度较小,胶囊平均速度最终维持在41 mm/s附近,系统维持单周期单碰撞响应状态,见图11(e)、图11(g)与图11(k)、图11(m)。当mm超过7 g时,见图11(h)、图11(n),vavg变为约30 mm/s,此时,激振体与壳体不再发生碰撞,胶囊只随肠道蠕动;主要原因是当激振体质量持续增大时,将导致库伦摩擦力过大,激振冲击力小于外界阻力,胶囊无法相对小肠移动。另外,对激振质量块质量变化时,胶囊的多稳态进行了分析,见图11(a)、图11(b),令mm由高到低进行变化,由图11(f)、图11(l)可知系统的阶跃点由之前的7 g变为5.9 g,且存在明显的迟滞回线。 接着,分析激振体的刚度k1对胶囊系统动态响应的影响,k1的变化区间设置为[10 N/m,120 N/m],参数间隔为0.05 N/m,结果如图12所示。特别地,刚度k1过小时系统会出现混沌现象,见图12(i),此时胶囊的平均速度为32.5 mm/s,见图12(c)。当k1=12 N/m时,系统响应为的单周期单碰撞状态,速度达到最大为44.9 mm/s,见图12(d)、图12(j)。随着k1继续增大至68 N/m,vavg逐步下降至30 mm/s,见图12(e)~图12(g),响应保持在单周期单碰撞,但碰撞逐渐减弱,见图12(k)~图12(m)。当k1>68 N/m时,碰撞消失,胶囊的移动速度稳定在30 mm/s,即仅依靠肠道蠕动实现前进,见图12(h)~图12(n)。 图12 关于激振块刚度k1的动力学分析(图12(c)~图12(b)中虚线表示胶囊外壳,实线表示激振体;图12(i)~图12(n)中竖线为撞击面位置,圆点为庞加莱截面截取的点)Fig.12 Dynamic analysis of oscillator stiffness (1) 本文通过考虑小肠的应力应变特征与其蠕动规律,建立了小肠-胶囊耦合动力学模型,重点讨论了胶囊的振幅、频率、激振体刚度与质量4项参数对胶囊在小肠内移动的影响。由于所建立的动力学模型耦合了自推进胶囊自身的接触非线性以及小肠阻力的非线性特征,因而在系统的非线性动力学行为规律研究中发现了倍周期分岔、逆倍周期分岔、混沌等现象,它们对胶囊的自推进移动影响显著。 (2) 当调节激振参数时,胶囊的振动形式主要表现出单周期单碰撞、单周期双碰撞、双周期单碰撞、双周期双碰撞4种状态;从胶囊的平均移动速度来看,最优的前进速度都出现在单周期单碰撞的振动状态下,原因在于单周期单碰撞能更高效地实现能量集中并通过激振体对壳体的唯一一次碰撞,最大程度地将激励能量转化为驱动冲击力。此外,在给定的参数范围内,当振幅增大时,胶囊始终保持相对小肠正向运动,胶囊的绝对速度持续增加并最终稳定在44 mm/s左右;而频率变化过程中会出现胶囊相对小肠反方向移动的情况(f处于15 Hz附近时),此时胶囊处于单周期双碰撞状态。此外,频率过高时,会导致激励驱动失效,胶囊表现为相对静止,只随小肠蠕动前进。综上,在调节胶囊激振参数时,应保证系统在稳定的单周期单碰撞状态;而要使胶囊实现反向移动,则需要对频率进行调整,使胶囊处于单周期双碰撞状态;此外,还应注意避免由于激励频率过高而导致的驱动失效。 (3) 相比于激振参数,改变结构参数时胶囊基本保持在单周期单碰撞、单周期双碰撞与混沌3种状态下,其中混沌与单周期双碰撞分别只出现在k1与mm极小时,胶囊的最优前进速度分别出现在mm=7 g与k1=12 N/m附近时,系统状态都为单周期单碰撞状态。此外,胶囊的反向移动仅出现在mm极小时,此时系统为单周期双碰撞状态,与调节激振频率时发现的规律一致。此外,在对胶囊结构进行设计时,应避免激振体质量过大或刚度过大而导致的驱动失效。 (4) 本文现有的分析与结论,都建立在对胶囊的单参数分析之上,接下来将考虑对胶囊多个参数同时进行分析并进行多目标优化,在平均速度的基础上增加能耗、以及肠道损伤度等优化目标;并进行可靠性分析,以此来制定更为合理的激振控制方案与胶囊结构设计,从而更好地指导后续的试验研究。
1.2 小肠模型
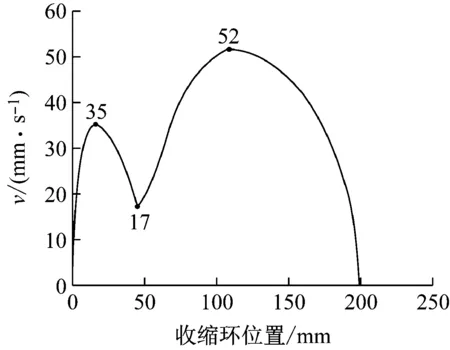
1.3 小肠阻力模型
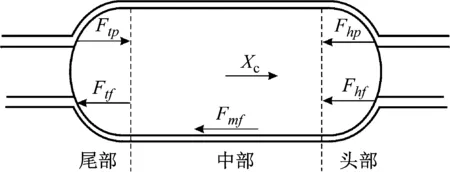
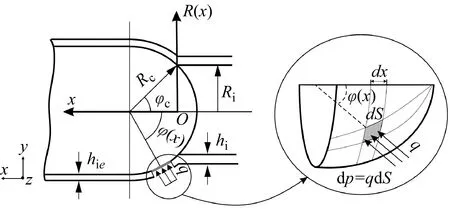
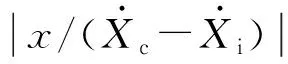

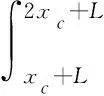
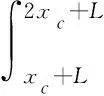
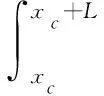
1.4 自推进胶囊的动力学模型
2 非线性动力学分析

2.1 激振参数的影响
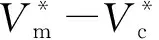
2.2 结构参数的影响
4 结 论

