悬索光伏支架结构抗风设计方法初探

蔡 元， 邓 华， 李本悦

(1. 浙江大学 空间结构研究中心， 杭州 310058； 2. 浙江大学 平衡建筑研究中心， 杭州 310028；3. 浙江大学建筑设计研究院有限公司， 杭州 310028)

光伏发电是利用半导体界面的光生伏特效应将光能直接转化为电能的一种绿色、可再生的发电技术[1]。近年来，光伏发电产业发展迅速，电站建设数量和规模不断增加，但占地量大的问题也突现。在土地资源紧张的地区，光伏电站的建设往往需要利用污水处理厂、苗木林地等面积相对较大的空旷场地。由于不能影响这些建设场地的既有生产，一般要求光伏支架的支承跨度达到十余米到数十米。如果采用常规的钢型材或铝型材支架，其造价将引起光伏电站的建设成本大幅上涨，降低上网电价的竞争力。近年来，以悬索结构为代表的新型柔性支架[2]在光伏电站建设中被较多使用。此类支架形式具有造价低、跨越能力强的优点，但较弱的刚度也使结构在风荷载作用下易产生较大的变形，甚至引起光伏组件的破坏。因此考察其风致响应特点并提出有效的抗风设计方法是值得研究的问题。

目前针对悬索光伏支架结构的抗风研究基本是空白的。马文勇等[3-4]通过刚性模型的风洞测压试验研究了光伏组件表面风荷载的分布规律，提出了建议的风荷载取值模型。徐志宏等[5]沿用常规刚性结构的风振系数法[6]分析了鱼腹式索桁架光伏支架结构的风致响应。但是，悬索结构是一种典型的非线性结构[7]，风荷载作用下结构的动力分析以及响应规律较为复杂。特别是出于降低端部支承框架以及基础造价的考虑，悬索中施加的预应力水平一般并不高，结构的非线性特点进一步增强。这使得常规风振系数形式的抗风设计方法及基于振型分解的频域分析方法不再适用。结构较柔的刚度还可能引起风与结构的流固耦合效应[8]，甚至导致气动失稳。但应该看到，悬索光伏支架结构形式简单，影响结构风致响应的参数并不多，因此可以通过一定规模的参数分析来考察结构的风致位移和内力响应特点，并归纳出适用于此类非线性结构的抗风设计方法。

本文将利用向量式有限元法进行悬索光伏支架结构的非线性动力响应计算。基于代表性模型，分析结构风致位移和内力响应的特点。考察结构跨度、预应力、索截面面积、基本风压、光伏板倾角等参数对结构风致响应的影响。最后利用分析结果，提出一种悬索光伏支架结构抗风设计实用方法。

1 结构模型及动力分析方法

1.1 悬索光伏支架结构

典型的单跨悬索光伏支架结构示意图，如图1(a)所示，工程中也常采用连续多跨布置的形式。每行光伏板由间隔0.6 m的两根悬索支承，光伏板的尺寸规格为1.65 m×1.00 m，质量为18.5 kg，与水平面的夹角θ通常为15°～45°。相邻光伏板间的净空一般为0.2 m。悬索固定于两端钢框架上，通常利用锚固于地面的背索来平衡悬索拉力。目前工程中，悬索光伏支架结构的跨度L一般为8～24 m，索采用公称直径为10～20 mm的钢丝绳。在考虑光伏板和结构自体质量时，索拉力通常为6～24 kN。

(a) 支架结构布置

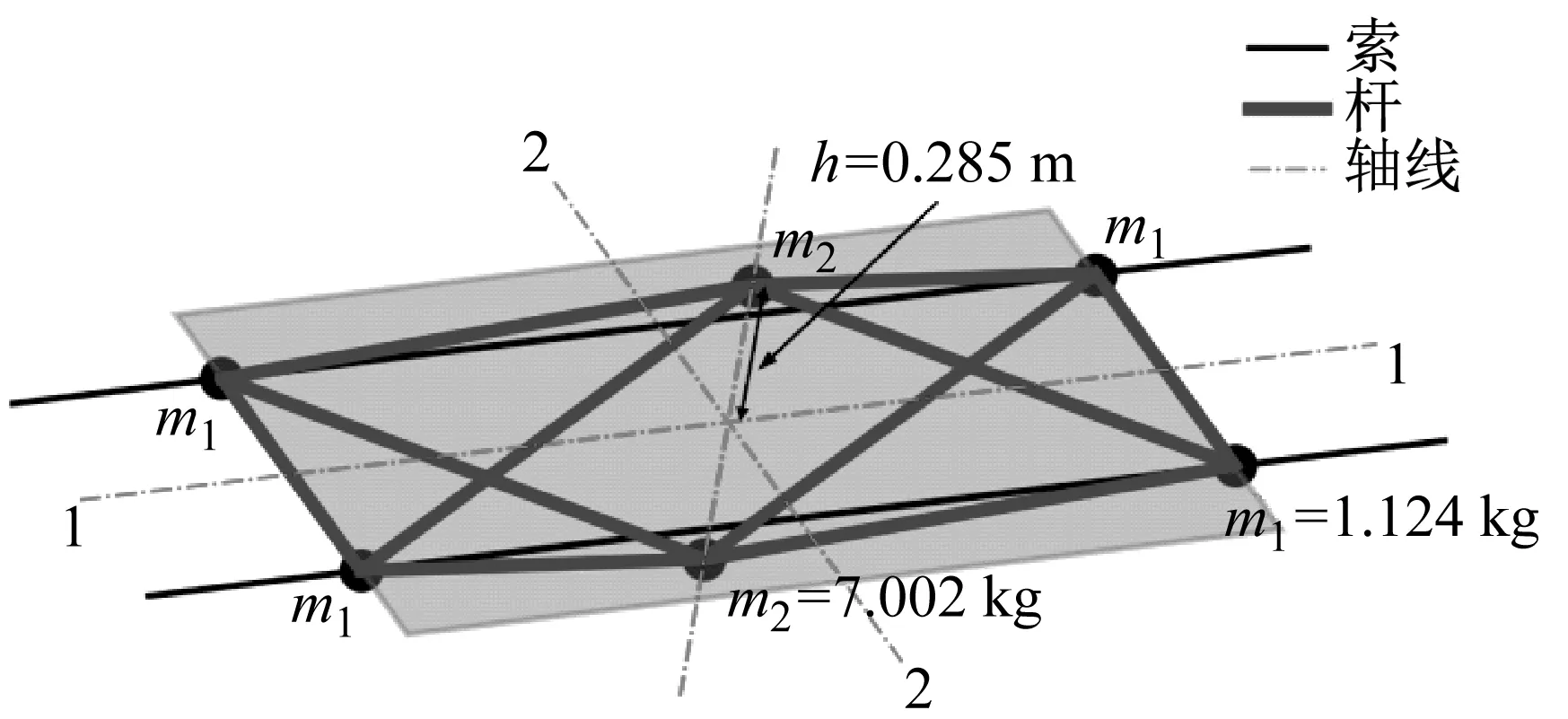
(b) 光伏板的向量式有限元计算模型图1 悬索光伏支架结构Fig.1 Cable-suspended photovoltaic module support structures

1.2 向量式有限元计算模型

考虑悬索光伏支架结构刚度较弱、非线性较强，采用向量式有限元法[9-10]进行结构风致动力响应分析。选择图1(a)中的一行光伏支架作为分析模型。为方便计算，采用图1(b)所示的10个沿光伏板面对称布置的杆单元来模拟一块光伏板，并对杆单元赋予相对较大的轴向刚度(EA=5×104kN)。根据文献[11]的分析，该简化模型中杆单元对索的轴向变形影响很小，同时可以考虑光伏板对两根支承索的变形协同约束。根据总质量以及沿轴1、轴2的转动惯量相等的原则，将光伏板的质量等代为图1(b)所示的6个节点集中质量。

假定悬索在两端钢框架上的锚固点为固定铰支座，并通过改变悬索的无应力长度(原长)来调节预应力水平。索采用只承受拉力的杆单元模拟，在光伏板的集中质量点处分段，取弹性模量E=95 GPa。结构阻尼采用仅包括质量项的Rayleigh阻尼，令阻尼比ξ=0.01。

1.3 风荷载

假设水平脉动风速符合Davenport谱[12]

(1)

Cohij=

(2)

(a) 脉动风速时程

(b) 功率谱图2 模拟的脉动风速Fig.2 Simulated fluctuating wind velocity

忽略作用于索上的风荷载，并假设作用于光伏板上的风荷载沿垂直板面方向平均分配到4个索上集中质量处。不考虑风与结构的流固耦合效应，且引入准定常假定，则单个集中风荷载为

(3)

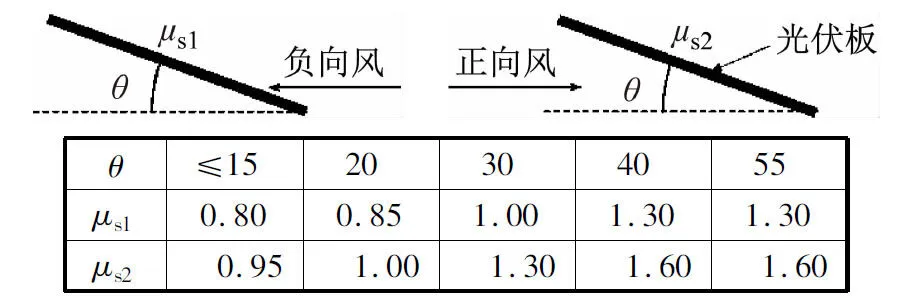
注：中间值按线性插值法计算。图3 光伏板风荷载体型系数Fig.3 Shape factor of wind load on photovoltaic panels

应该指出，悬索支架的刚度会随着结构形状和内力的改变而发生变化。由于正、负向风荷载的方向和大小不同，光伏板及结构自体质量与其组合的有利程度也不一样，结构在正、负向风荷载作用下的非线性响应特点将存在一定差异。

2 结构的风致响应特点

2.1 结构的动力特性

以结构在光伏板和索自体质量作用下的平衡状态为风荷载效应分析的参考构型。在该构型下，结构的前8阶振型及其频率fg，如图4所示。可知，前8阶振型以竖向振型为主，但也出现了2阶水平振型(第3、第7阶)和1阶扭转振型(第4阶)。虽然结构的刚度较弱，但是由于光伏板质量轻，结构的基频相对常规结构并不低，各阶模态频率分布的密集性并不高。

(a) 第1阶，竖向对称，fg=1.83 Hz

(b) 第2阶，竖向反对称，fg=3.46 Hz

(c) 第3阶，水平向对称，fg=3.89 Hz

(d) 第4阶，扭转，fg=4.82 Hz

(e) 第5阶，竖向对称，fg=5.31 Hz

(f) 第6阶，竖向反对称，fg=7.25 Hz

(g) 第7阶，水平向反对称，fg=7.71 Hz

(h) 第8阶，竖向对称，fg=9.33 Hz图4 结构前8阶模态的振型及频率Fig.4 Mode shapes and frequencies of the first eight modes of the structure

2.2 结构的风致响应

(a) 跨中节点z向位移

(b) 跨中索单元内力图5 结构响应Fig.5 Structural responses

(a) 跨中节点

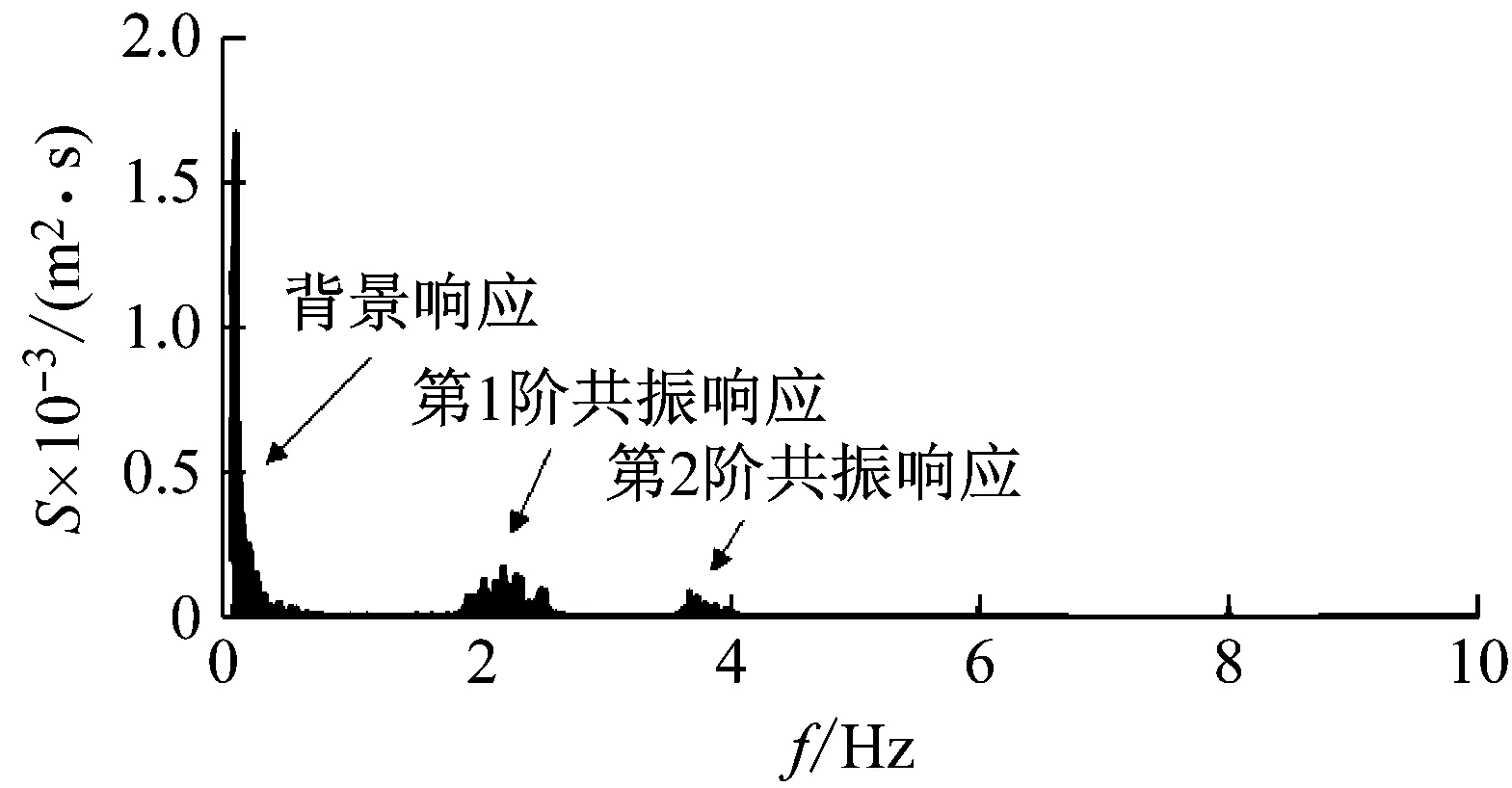
(b) 1/4跨节点图6 节点z向位移功率谱Fig.6 Power spectral densities (PSD) of z-direction nodal displacements

2.3 结构的风致响应标准差

采用统计学方法分析悬索光伏支架结构的风致响应特点。不同预应力水平下结构跨中节点z向位移的统计直方图，如图7所示。图7(a)～图7(c)中，平均风位移和位移平均值分别为48.74 cm和48.32 cm，27.50 cm和27.53 cm，17.77 cm和18.05 cm。表明直方图并非完全对称，而是随着预应力的增大逐渐向右偏移。注意到，设计验算时通常只需要考虑节点位移时程中大于平均风响应的部分，因此可以定义如下节点位移响应的单边标准差

(a) H=7 kN

(b) H=15 kN

(4)

不同预应力水平下结构跨中索单元内力的统计直方图，如图8所示。图8(a)～图8(c)均向右偏移，且随着预应力的增大，右偏程度增加。与位移响应相似，定义单元内力响应的单边标准差

(a) H=7 kN

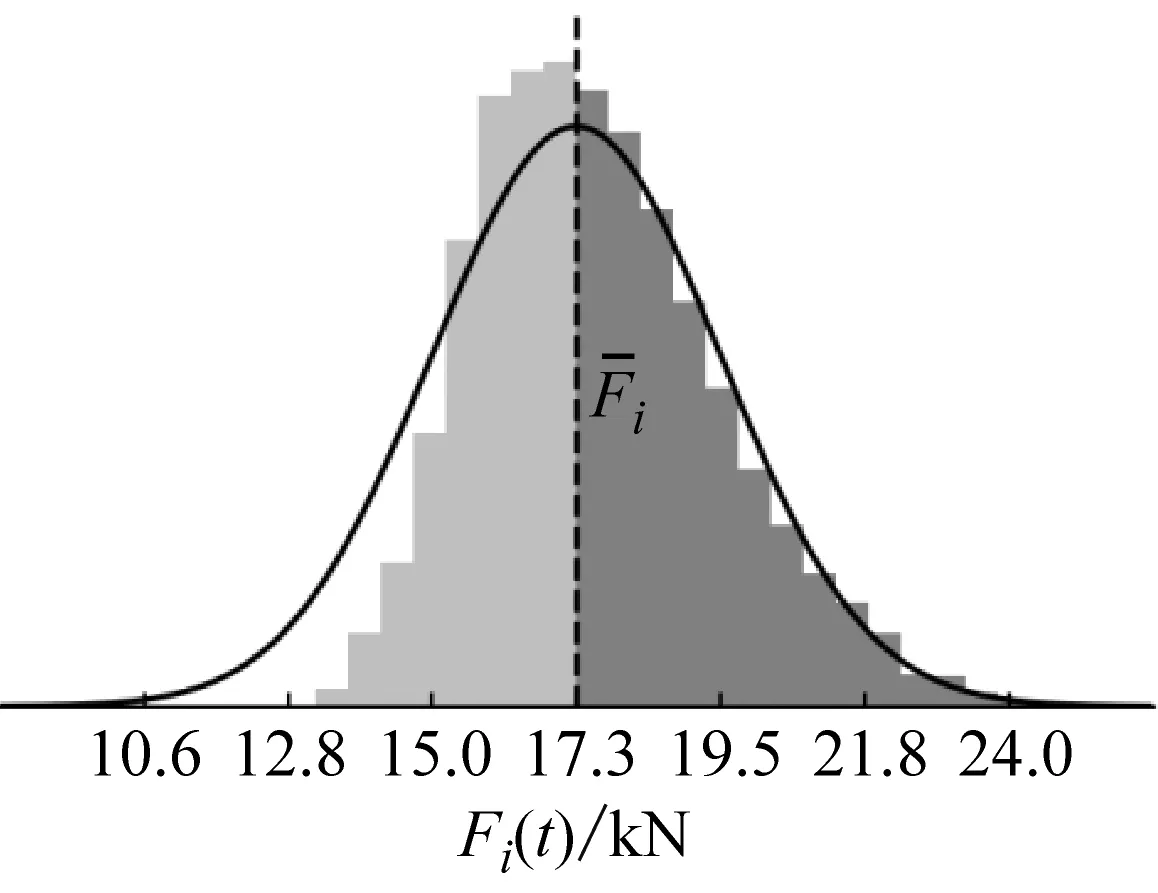
(b) H=15 kN

(c) H= 25 kN图8 跨中索单元内力的统计直方图Fig.8 Statistical histograms of internal force of the mid-span cable element

(5)

3 影响结构风致响应的参数分析

3.1 预应力

改变基本结构模型的预应力，求得的节点z向位移标准差σui和单元内力标准差σFi沿跨度的分布，如图9所示。其中跨中节点位移和单元内力的具体计算结果，如表1所示。

(a) 节点z向位移标准差

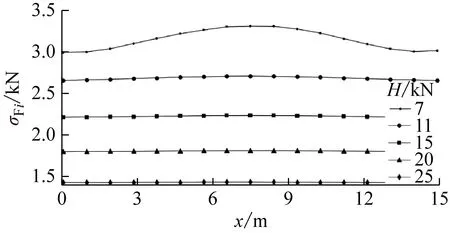
(b) 索单元内力标准差图9 结构响应标准差沿跨度的分布Fig.9 Standard deviation distributions of structural responses along the span

表1 对应于不同预应力水平的结构响应特征Tab.1 Characteristics of structural responses corresponding to different prestress

表A.1 主要参数说明Tab A.1 Description of main parameters

如图9(a)所示，随着预应力的增加，结构刚度增大，节点z向位移标准差σui总体上趋于减小。但是对于H=7 kN的较低预应力水平的情况，跨中节点的σui(记为σu)反而小于更高预应力水平的结构模型。对平均风作用下结构的平衡构型进行分析，发现H=7 kN时结构垂度更大，弹性刚度对竖向刚度提供较大的贡献[19]。由表1可知，平均风作用下H=7 kN结构的基频fw反而大于H=11～20 kN的情况，也说明其竖向刚度较大。

由图9(b)可知，随着预应力的增大，σFi也呈现出减小的趋势，且各单元的σFi沿跨度的变化趋于平缓。在各种预应力水平下，跨中索单元的σFi(记为σF)均为最大，可用于表征悬索的内力变化。

3.2 索截面面积

保持基本结构模型的H=15 kN不变，当悬索分别采用公称直径Φ10～Φ18的钢丝绳时，相应的结构风致响应分析结果，如表2所示。由表2可知，索截面面积A越大，结构刚度越大，跨中节点z向位移标准差σu越小，但是平均风引起的跨中节点z向位移uw却几乎不随A变化。实际上，A越大的索自体质量越大，保持H不变时参考构型的垂度越大。参考构型的降低抵消了刚度增大的影响，使得uw的变化不明显。此外，计算结果表明，索截面面积A越大，跨中索单元的内力标准差σF和平均风作用下跨中索单元内力相比参考构型时的增量Fw越大。

表2 对应于不同索截面的结构响应特征Tab.2 Characteristics of structural responses corresponding to different cable cross sections

3.3 结构跨度

保持基本结构模型的索截面面积A和预应力水平H不变，当结构跨度L取7.6～22.4 m时，相应的结构风致响应计算结果，如表3所示。由表3可知，随着跨度L的增大，结构的刚度减小，σu和σF均增大。

表3 对应于不同跨度结构的响应特征Tab.3 Characteristics of structural responses corresponding to different spans

3.4 光伏板倾角

当基本结构模型的光伏板倾角θ取10°～45°时，结构风致响应分析结果，如表4所示。随着θ的增大，体型系数μs增大，导致风荷载增大，同时风荷载方向与z轴的夹角也增大。节点的z向位移受到风荷载大小和方向的综合影响。由表4可知，当θ≤30°时，两方面因素基本抵消，σu几乎不随θ而变化；当θ>30°时，风荷载方向的变化起主导作用，σu随θ的增大而减小。由于索单元内力几乎不受风荷载方向的影响，故表4中σF随θ的增大而增大。

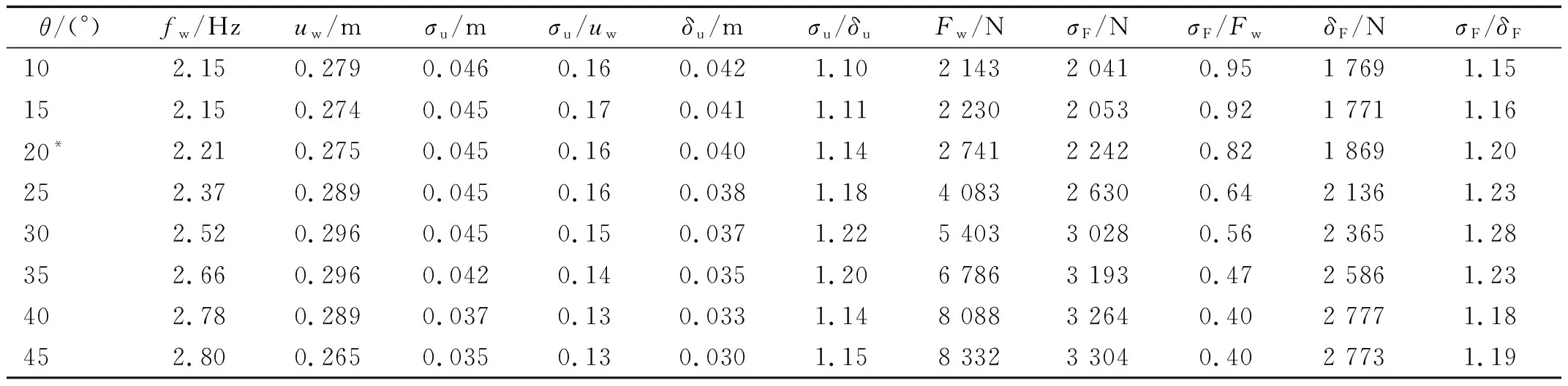
表4 对应于不同倾角θ的结构响应特征Tab.4 Characteristics of structural responses corresponding to different θ

3.5 风速

对基本结构模型施加不同平均风速的正向和负向风荷载，结构的风致响应分析结果，如表5所示。总体来看，随着平均风速的增大，结构的所有响应均增大。造成正向和负向风作用下结构响应差异的主要原因在于体型系数μs的大小以及风荷载与结构自体质量组合的方式。由图3可知，正向风荷载的μs更大，相同平均风速时的风荷载脉动分量比负向风大，因此结构响应标准差σu，σF更大。虽然正向风荷载的μs大于负向风，但由于与结构自体质量方向相反，结构在正向风作用下受到的总荷载反而小，因此其平均风引起的跨中索单元内力增量Fw较小。此外，在正向风作用下，结构位移还包括了风荷载克服结构自体质量产生的部分，故正向平均风引起的跨中节点z向位移uw相对于负向风更大。

表5 基本结构模型在不同风荷载作用下的响应特征Tab.5 Characteristics of structural responses of typical model under different wind loads

4 简化设计方法

4.1 准静力响应的标准差

目前GB 50009—2012《建筑结构荷载规范》[20]采用风振系数来放大平均风荷载或其效应，以考虑脉动风的影响。对于悬索光伏支架结构，跨中节点z向位移和单元内力的风振系数可分别定义为

(6)

(7)

式中，μu和μF为峰值保证因子。可以看出，风振系数设计方法是用结构的平均风响应近似估计动力响应标准差，其有效性依赖于σu(或σF)和uw(或Fw)可保持较稳定的比例关系。然而由表1～表5可知，当结构或荷载参数发生变化时，σu/uw和σF/Fw往往呈现出较大的离散性，且这种离散性主要是由悬索光伏支架结构的非线性特征引起的。以跨中节点位移为例，σu表征的是结构动力响应偏离平均风响应的程度，而uw反映的是平均风响应相对仅重力作用下参考构型的距离。从刚度的角度而言，uw主要受结构参考构型的刚度控制，而σu则取决于施加平均风后结构平衡构型的刚度。由于结构的非线性特性，以上两个构型的刚度往往存在显著差异，故造成uw和σu不成比例地变化。

前面对图5的分析已经指出，结构的风致动力响应主要与准静力响应的变化趋势一致，即两者相对平均风响应的偏差是相近的。因此，可尝试用准静力响应的标准差来近似估计结构动力响应的标准差。假设准静力荷载Pi(t)作用下结构的刚度始终与平均风作用下结构平衡构型的刚度相同，则结构的准静力响应与Pi(t)呈线性关系。进一步将式(3)按如下形式展开

(8)

(9)

(a) σu

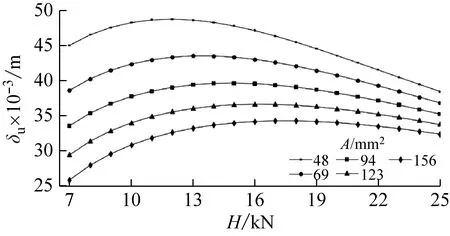
(b) δu

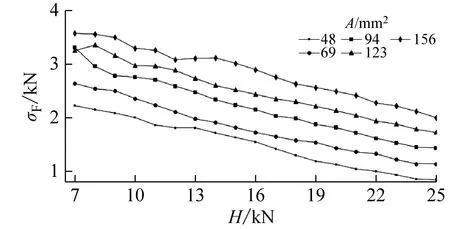
(c) σF

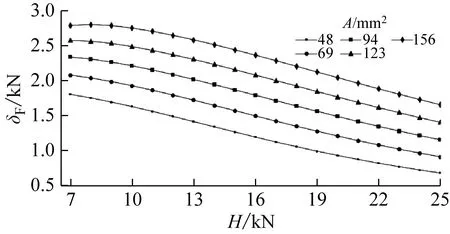
(d) δF图10 对应于不同索截面面积和预应力的结构响应特性Fig.10 Characteristics of structural responses corresponding to different cable’s cross-sectional areas and prestress

4.2 敏感性参数分析

表6 不同数量的参数对应的拟合精度Tab.6 The fitting accuracy corresponding to different numbers of parameters

(10)

(11)

4.3 风致响应设计公式

u=uw+μuσu

(12)

(13)

式中，峰值保证因子μu和μF可根据所需的保证率按正态分布取值。

5 结 论

(1) 悬索光伏支架结构的风致响应以背景响应和低阶竖向模态的共振响应为主。

(2) 悬索光伏支架结构的风致位移和内力时程响应在概率分布上具有不对称性。面向结构设计验算，本文提出了仅考虑不利一侧响应的单边标准差计算方法，并指出可用正态分布函数近似分析位移和内力响应的保证率。

(3) 悬索光伏支架结构的风致动力响应标准差与其准静力响应的标准差相关。通过较大规模的样本回归，本文提出了由结构风致准静力响应标准差估算其动力响应标准差的拟合公式。

(4) 本文提出了一种悬索光伏支架结构的简化抗风设计方法。该方法只需计算结构在两种不同平均风作用下的静力响应，就能有效估算结构的风致动力响应。

(5) 本文的分析未考虑光伏板面板的弯曲刚度，忽略了风与悬索支架结构间可能存在的流固耦合效应，且引入了准定常假定来确定板面风荷载，但总结的结构风致响应特点及简化估算方法对于此类新型支架结构抗风设计方法的进一步研究有参考意义。