框架结构空间自参数共振的试验与数值研究

刘 伟， 沈 超， 于 越， 李遇春

(同济大学 土木工程学院， 上海 200092)

随着现代科学技术的发展，高强度材料和大长细比构件越来越多地应用于框架结构中。这些结构经常受到周期性荷载的作用，如水工建筑物表面的水流脉动压力、桥梁上行驶车辆的周期性荷载以及桥墩周围的周期性水流涡激力，在结构设计中这些必须考虑周期性荷载的动力效应。如果外力的激励频率接近结构的固有频率，结构会发生普通共振，工程师和研究人员已对这类普通共振问题有了充足的了解和研究。如果外荷载激励频率大约等于结构或子结构固有频率的两倍，框架结构可能会经历所谓的参数共振或自参数共振。参数共振对结构具有极大的危害性，但其潜在风险很容易被结构工程师忽视。因此，有必要确定框架结构在周期性荷载作用下的参数共振稳定边界，以避免潜在的参数共振动力失稳风险。

Bolotin等[1-8]对不同约束条件下单跨梁的参数共振动力失稳问题进行了深入的研究。

刘金建等[9]研究了轴向运动黏弹性二维纳米板结构的非局部横向参数振动及其稳态响应；杨宏康等[10]考虑静动液压引起的壳体应力刚化(软化)效应分析了基底隔震储液罐的参数动力稳定性；张登博等[11]研究了计及非齐次边界条件的面内变速运动黏弹性板的主参数振动稳态响应；陈舟等[12]对行人引起人行桥参数振动作用下的大幅振动进行了理论和数值分析；李云东等[13]采用数值方法研究了参数激励作用下非线性弹性地基上悬臂输流管道的参数动力稳定性；陈丕华等[14]采用理论和试验相结合的方法研究了斜拉索在弦向位移激励下的参数振动稳定性。上述结构动力稳定性问题的运动方程均可表示为齐次Mathieu-Hill方程，齐次Mathieu-Hill方程的不稳定解可用Bolotin方法或摄动法[15-16]求解。

框架结构可以由两个子结构组成，这两个子结构通过铰链连接，一个子结构是主系统，另一个是次系统。承受周期性外荷载的主系统会引发次系统的自参数共振，这种由主系统激发次系统的参数共振称为自参数共振。Tondl等[17]详细给出了机械系统自参数共振的具体定义；Náprstek等[18]研究了暴露于强垂直分量的易变形高层结构的自参数共振问题；Xia等[19]通过使用Lyaponov指数研究了斜拉梁结构在随机激励下的自参数共振稳定性。这些自参数共振问题的运动方程表示为非齐次Mathieu-Hill方程，因此不能直接通过Bolotin方法或摄动法求解。非齐次Mathieu-Hill方程的动力稳定性分析的一般方法是基于运动方程的时程解，Lyapunov指数已广泛运用于工程结构的参数共振动力失稳分析[20]。最近，Li等[21-23]提出了能量增长指数/系数(energy growth exponential/coefficient，EGE/EGC)来确定参数激励系统的稳定性边界。EGE/EGC所得到的稳定性边界与传统方法和试验所得的结果一致。

现有的参数振动研究表明，主参数共振(1/2次谐波)是最容易诱发和最危险的参数共振模式。其他参数共振模式，例如谐波参数共振和超谐波参数共振，在现实世界中很难发生，因此本文只研究了框架结构的主参数共振问题。

本文提出了一般框架结构空间自参数共振的数值预测方法，为了验证数值方法的正确性，进行了空间自参数内共振和非内共振试验。根据试验与数值预测结果确定和比较了框架结构的自参数内共振和非内共振的稳定边界，强调了空间自参数内共振的特殊性和危险性。

1 理论公式

1.1 考虑内轴力效应的梁单元空间运动方程

框架结构一般由几个均匀的梁单元组成，考虑图1所示局部坐标系oxyz中的均匀梁单元，其中：梁的初始长度为l，横截面积为A，质量密度为ρ，杨氏模量为E，剪切模量为G，极坐标绕x轴的转动惯量为J，绕y和z轴的转动惯量分别为Iy和Iz。对于节点i和j，局部坐标分别为(xi,yi,zi)和(xj,yj,zj)，节点位移分别为{μxi,μyi,μzi,θxi,θyi,θzi}T和{μxj,μyj,μzj,θxj,θyj,θzj}T,节点力分别为{Fxi,Fyi,Fzi,Mxi,Myi,Mzi}T和{Fxj,Fyj,Fzj,Mxj,Myj,Mzj}T。

(a) 节点位移

(b) 节点力图1 均匀梁单元的节点位移和力Fig.1 Nodal displacements and forces of a uniform beam element

基于哈密顿原理和Bernoulli-Euler梁的基本理论(忽略该梁的转动惯量和剪切变形)，在局部坐标系下考虑内轴力作用的梁单元运动方程可推导为[24-26]

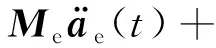
(1)

其中

(2)

式(1)可以改写为

(3)

其中

(4)

1.2 框架结构总体运动方程

将框架结构在局部坐标系中的所有单元运动方程(式(3)，e=1,2,3,…，N)都转换到总体坐标系下，然后将总体坐标系下的单元运动方程进行组装整合可以得到以下结构总体运动方程

(5)

(6)

C+βk·K

(7)

当具体研究结构第j阶模态的参数共振时，系数βk由下式计算。

(8)

式中，ωj和ξj分别为框架结构第j阶模态的自振频率和阻尼比。

1.3 时程解和稳定性分析

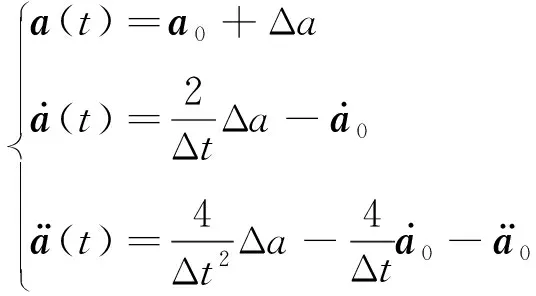
(9)

将式(9)代入式(5)可得到如下增量方程

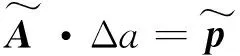
(10)

其中

(11)

需要注意的是，在上述推导中已经进行了近似KG(t0+Δt)≈KG(t0)。因此，结构的动态时程响应是通过求解式(10)获得的。

框架结构的机械能可以写作

[K-KG(t)]·a(t)

(12)

如果框架结构受到初始小扰动，则结构系统的初始能量可表示为E(t)|t=0=E0。框架结构的EGE可以定义为

(13)

式中，[t1,t2]为能量函数ln[E(t)]的主干曲线斜率线性增加的开始时间间隔，框架结构的稳定性可以通过以下标准判断

(14)

框架结构参数共振的稳定边界可由λ=0确定。

2 框架结构空间参数共振试验研究

2.1 试验模型和试验装置

如图2和图3所示，Γ形试验框架由水平梁(梁1)和竖直梁(梁2)组成，框架的几何尺寸如图4所示。通过自由振动试验测得了梁1和梁2的弹性模量E1=2.487×1011N/m2和E2=1.637×1011N/m2。梁1和梁2由钢铁制成，质量密度均为ρ=7 850 kg/m3。梁1和梁2横截面互相垂直并用铰链连接，即两根梁的连接端只释放了梁2的z方向转动自由度(见图4)。梁2的另一端夹在底板上，梁1的另一端铰接在支架上。两个集中质量块被选择性地连接在A点(梁1)和B点(梁2)，以调节梁1和梁2的基频。

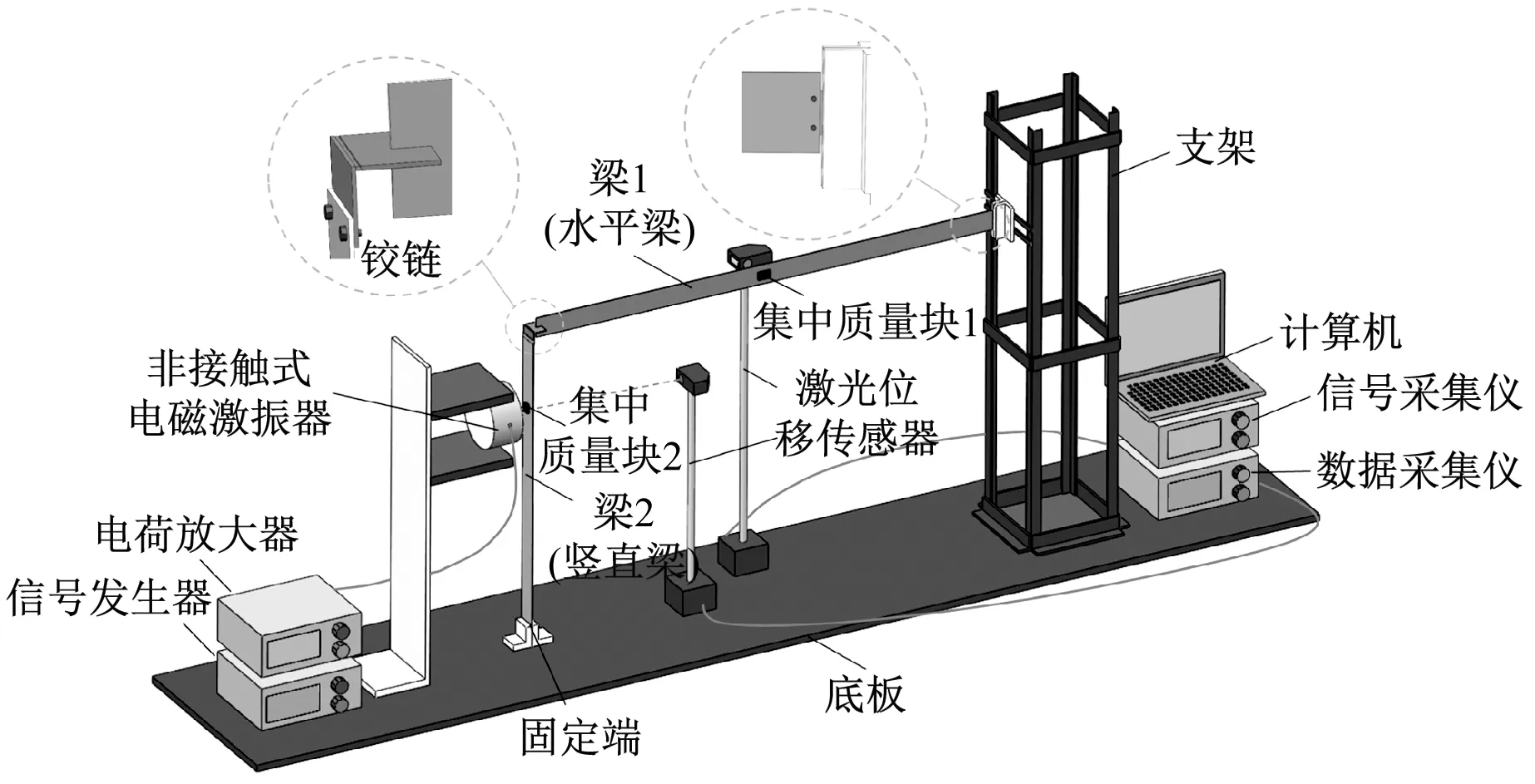
图2 试验示意图Fig.2 Experimental schematic diagram

图3 试验装置照片Fig.3 Photo of experimental facilities

图4 试验模型几何尺寸 (mm)Fig.4 Geometric diagram of test model (mm)

如图2和图3所示，周期性力信号由信号发生器(EM32000A/B)产生，由功率放大器(GF100)放大，最后传输到非接触式电磁激振器(DJ-20)。该激振器在梁2的B点上提供周期性的电磁荷载，用激光位移传感器(SUNX-ANR1215)测量B点的位移，这可以看作是梁1的位移激励，另一个激光位移传感器用于测量梁1中点A的位移响应。两组位移响应信号由数据采集仪(INV306U-A)同时采集，信号分析仪(INV306U)分析后由计算机记录。

在试验模型中，梁2和梁1可以分别视为主系统和次系统。电磁激振器激发梁2振动后，通过铰链将周期性轴向力从梁2传递到梁1，从而引起梁1的空间自参数共振。

2.2 空间自参数内共振试验(工况1：fe≈f02≈2f01)

在该工况下，A点和B点处的附加质量分别为8.5 g和36 g。符号fe、f01和f02分别为电磁激振器的激励频率、梁1的基频和梁2的基频。梁1和梁2的频率关系设计为f02≈2f01。用自由振动法可以得到梁1和梁2的实测自振频率和阻尼比，数值自振频率可用有限元方法计算，试验模型的模态参数如表1所示。

表1 试验模型的自振频率和阻尼比(工况1：内共振)Tab.1 The natural frequency and damping ratio of the test model (case 1: internal resonance)

在该工况下fe≈f02≈2f01，使用电磁激振器在梁2的B点施加周期性载荷，并使用激光位移传感器同时测量A点和B点的位移时程响应。在本试验中不能直接测量激振力(磁力难以测量)，但根据结构动力学的知识，可以通过测量梁2上B点的位移响应来间接获得激励力。

图5显示了试验模型的典型空间自参数内共振响应，其中激励频率设置为fe=8.18 Hz≈f02≈2f01。图5(a)表明了梁2(主系统)的x方向(面内)位移响应幅值在初始阶段线性增加，然后由于结构阻尼效应达到稳定值，梁2的响应频率近似等于激励频率。结果表明，梁2发生了典型的普通共振。从图5(b)可以看出，梁1的不稳定运动是由梁2的普通共振激发的，梁1(次系统)的面外(z方向)位移振幅呈指数增大，梁1的响应频率为4.14 Hz，约为激励频率的一半，这表明梁1发生了典型的(1/2次谐波)自参数共振。这种由主系统(梁2)的普通共振激发的次系统(梁1)的参数共振动力失稳称为自参数内共振。由于几何非线性效应，梁1最终达到稳态振动，这被称为参数共振的“极限环振荡”。工况1的内共振试验视频可以通过以下链接进行观察：https:∥www.bilibili.com/video/BV1M54y1a7eQ/.

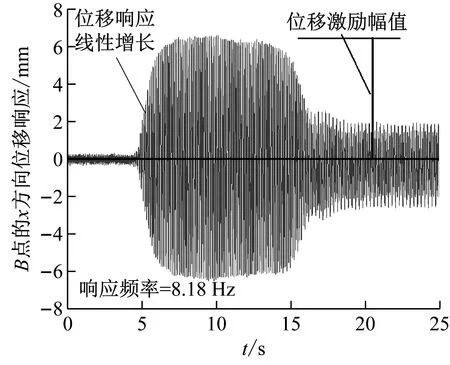
(a) 梁2的面内(x方向)位移响应(作为梁1的位移激励)

(b) 梁1的面外(z方向)位移响应图5 自参数内共振试验典型数据(工况1：fe≈f02≈2f01)：Fig.5 A typical measured displacement response of autoparametric internal resonance (case 1:fe≈f02≈2f01)

在试验中，首先固定了电磁激振器的激励振幅，梁2(主系统)的稳态位移响应振幅被视为激励振幅(见图5(a))。然后不断增大(或减小)激励频率(频率阶跃=0.01 Hz)，直到梁1(次系统)的不稳定响应开始出现或消失。当梁1的位移响应从保持微幅振动到突然非线性增长时，即说明梁1发生开始发生参数振动动力失稳。同理当梁1从大振幅参数振动(极限环振荡)到位移响应迅速较小然后保持稳定，说明梁1结束参数共振动力失稳。将梁1开始失稳和结束失稳的两个频率分别视为下临界频率边界点和上临界频率边界点，最终通过确定不同激励幅值下的临界频率边界点可得到梁1空间自参数内共振的实测不稳定边界。

2.3 空间自参数非内共振试验(工况2：f02≠2f01, fe≈2f01)

在此试验工况下，A点和B点的附加质量分别为8.5 g和18 g，频率关系设计为f02≠2f01，试验模型的模态参数，如表2所示。

表2 试验模型的自振频率和阻尼比(工况2：非内共振)Tab.2 The natural frequency and damping ratio of the test model (case 2: noninternal resonance)

当外荷载激励频率为fe≈2f01(f02≠2f01)时，典型的试验位移激励和参数共振响应，如图6所示。在周期性外载荷作用下，梁2发生了有界强迫振动(见图6(a))，这导致了梁1的参数共振(见图6(b))。梁1的位移响应幅值呈指数增长，响应频率为4.09 Hz，约为激励频率的一半。这种由梁2的强迫振动激发的梁1的参数共振动力失稳称为自参数非内共振。工况2的空间自参数非内共振视频可通过以下链接观察：https:∥www.bilibili.com/video/BV1ri4y1 N7ZT/.

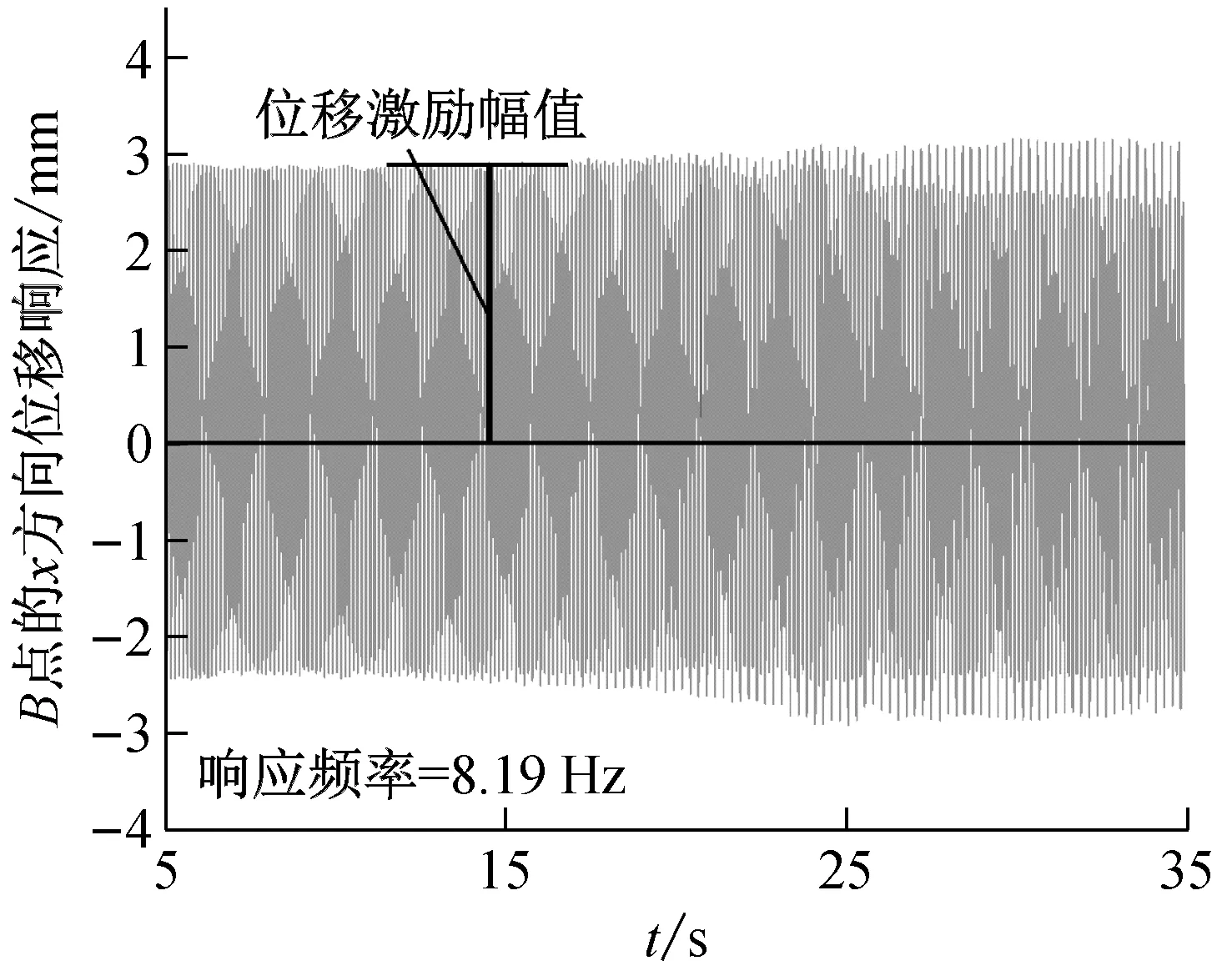
(a) 梁2的面内(x方向)位移响应

(b) 梁1的面外(z方向)位移响应图6 自参数非内共振试验典型数据(工况2：f02≠f01,fe≈2f01)Fig.6 A typical measured displacement response of autoparametric noninternal resonance (case 2:f02≠f01,fe≈2f01)

3 数值计算结果与试验结果的比较

3.1 力激励与位移激励的理论转换关系

如图4所示，对试验框架结构在B点施加x方向的周期力F=F0cos(2πfet)，相应的结构整体有限元方程(式(5))可以根据工况1和工况2的模态参数建立。我们可以通过求解运动方程(式(5))来获得B点的位移响应，其中位移响应的稳态振幅由D0表示。

在本试验中，由于使用非接触式电磁激振器，激励力(磁力)不能直接测量，因此梁2的位移响应(B点)D0被用作外部位移激励。然而在结构动力学分析中，我们习惯于使用力激励作为外部激励。因此，为了便于激励力和位移响应的换算，有必要给出激励力和位移响应之间的理论关系。根据结构动力学中力和位移的转换关系，如图7(a)和图7(b)所示的点线图，可以分别获得工况1和工况2的幅值比R0=D0/F0随激励频率fe的变化曲线。通过图7所给出的转换曲线，我们可以将试验测得的位移激励不稳定边界点转化为力激励不稳定边界点。

(a) 工况1

(b) 工况2图7 B点位移激励与力激励的幅值比Fig.7 The amplitude ratio of displacement excitation and force excitation at point B

3.2 数值稳定边界与试验结果的比较

3.2.1 空间自参数内共振的数值稳定边界(工况1)

在工况1中，首先在梁1的A点上施加z方向初始静力P=0.005 N，得到框架的初始静位移响应作为初始扰动。然后，对梁2的B点施加x方向周期力F=F0cos(2πfet)，相应的位移响应可通过式(5)求解。图8是一个典型的例子，其激振力的幅值和频率分别为F0=0.13 N和fe=2×f01=2×4.11=8.22 Hz。图8(a)显示了梁2上B点的位移响应，这也被视为梁1的位移激励。梁2的理论位移响应与试验结果相似(见图5(a))，是一种典型的普通共振响应。图8(b)显示了梁1的理论自参数内共振响应，这与图5(b)中的实测失稳过程也是一致的。

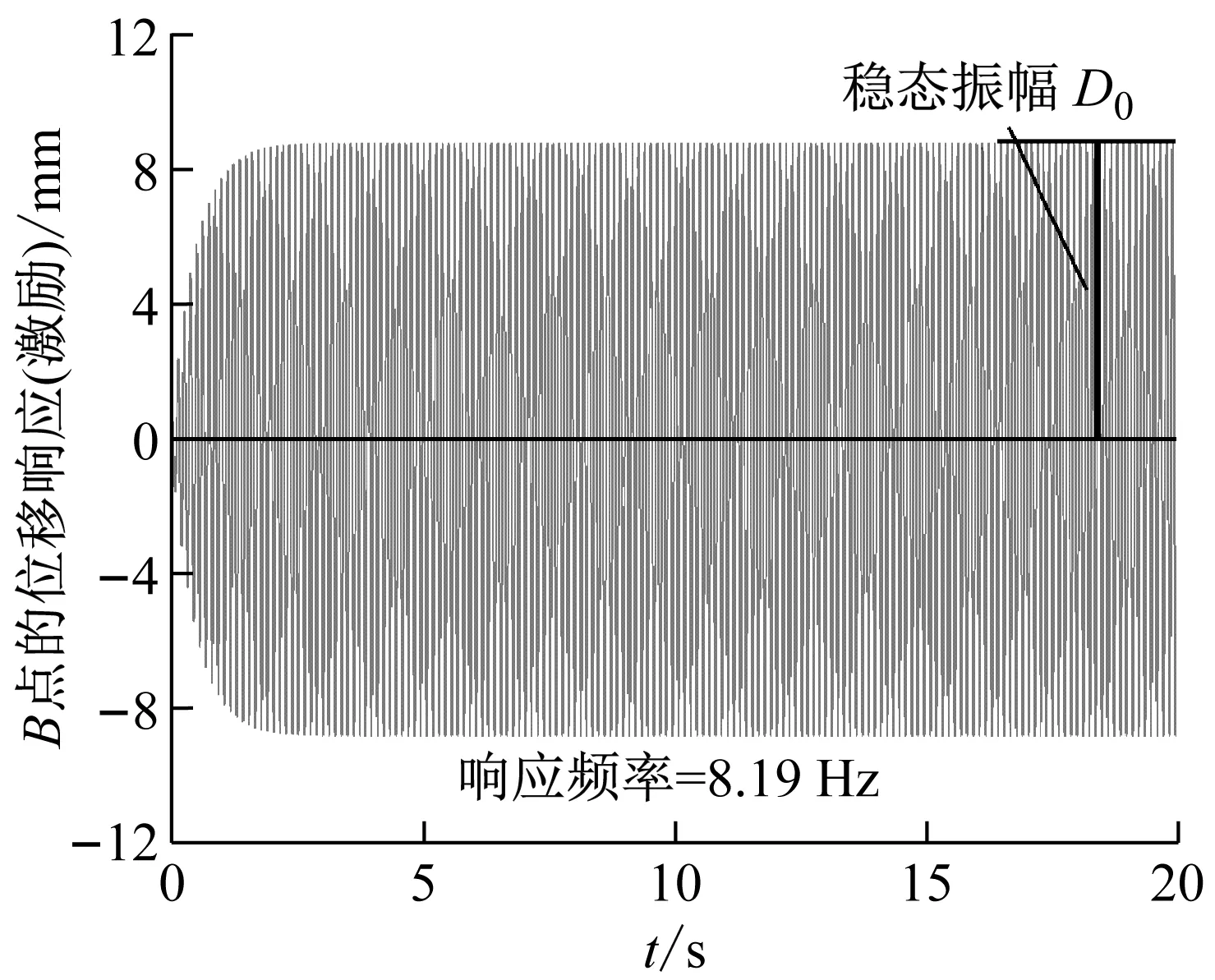
(a) 梁2

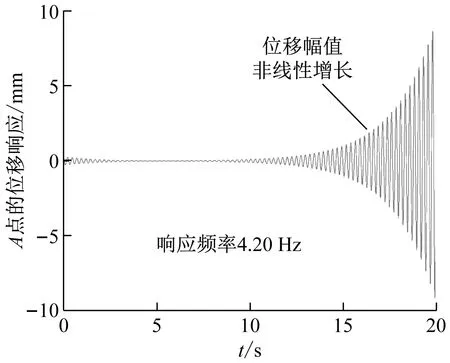
(b) 梁1图8 自参数内共振的数值位移响应(工况1)Fig.8 The numerical displacement responses of autoparametric internal resonance (case 1)

这里需要注意的是，式(5)是一个线性化的有限元方程，仅用于模拟结构的初始失稳过程(处于小变形状态)。当结构位移响应增大时，非线性项(在式(5)中忽略)将抑制结构响应幅值的无限增加，位移振幅将在有限范围内有界(见图5(b))。梁1和梁2之间的非线性相互作用反过来影响梁2的位移响应，这种非线性相互作用效应可以从图5(a)中15～25 s的位移响应中看出，这是不能用式(5)模拟的。结构振动的非线性仿真是一个非常复杂的问题，需要进一步研究。

对于确定的力激励幅值F0，可以通过改变激励频率fe来确定与EGE为零时相对应的频率点。该坐标(fe,F0)就是结构理论不稳定边界上的一点。试验框架参数共振的理论不稳定边界(参数共振动力失稳区域)如图9所示。当以位移作为激励时，将位移响应的稳态振幅D0(图8(a))作为激励振幅(位移激励)。可以得到在结构不稳定边界上的激励点(fe,D0)。梁1在位移激励下的理论不稳定边界(参数共振动力失稳区域)如图10所示，其中空心圆表示实测值，可以发现理论边界与试验边界吻合较好。

图9 梁1自参数内共振的数值稳定边界(工况1：力激励)Fig.9 Numerical autoparametric internal resonance stability boundary of beam-1 (case 1: force excitation)

图10 梁1自参数内共振的数值稳定边界(工况1：位移激励)Fig.10 Numerical autoparametric internal resonance stability boundary of beam-1 (case 1: displacement excitation)

3.2.2 空间自参数非内共振的数值稳定边界(工况2)

对于工况2，图11显示了试验框架典型的自参数非内共振的数值位移响应，其中激励力的幅值和频率分别为F0=0.2 N和fe=2×f01=2×4.11=8.22 Hz。图11(a)显示了梁2上B点发生了典型的强迫振动位移响应，梁2的理论位移响应类似于图6(a)中的实测位移响应。图11(b)显示了梁1发生了自参数非内共振响应，与图6(b)中的实测不稳定过程基本一致。梁1的理论不稳定边界计算过程与工况1相同，工况2在力激励和位移激励下的参数共振失稳区域，分别如图12和图13所示。图13表明，结构自参数非内共振不稳定边界与实测不稳定边界吻合较好。

(a) 梁2

(b) 梁1图11 非内共振数值位移响应(工况2)Fig.11 The numerical displacement responses of noninternal resonance (case 2)

图12 梁1自参数非内共振的数值稳定边界(工况2：力激励)Fig.12 Numericalautoparametric noninternal resonance stability boundary of beam-1 (case 2: force excitation)

图13 梁1自参数非内共振的稳定边界(工况2：位移激励)Fig.13 Numerical autoparametric noninternal resonance stability boundary of beam-1 (case 2: displacement excitation)

3.2.3 空间自参数内共振与非内共振不稳定边界的对比

根据3.1节中激励力与激励位移的理论关系，我们可以将图9和图12中的试验位移激励转换为相应的力激励，并重新绘制成图14中的不稳定边界，从中可以发现自参数内共振的不稳定区域比自参数非内共振的不稳定区域大得多。对于前者，由于梁2的普通共振的放大效应，较小的激励可以激发梁1的大振幅自参数共振，因此自参数内共振比非内共振破坏性大得多，在工程设计中应注意避免该工况。

图14 空间内共振与非内共振稳定边界的比较(工况1和 工况2：力激励)Fig.14 Comparison of stability boundaries between spatial internal resonance and noninternal resonance (cases 1 and 2: force excitation)

4 结 论

本文基于哈密顿原理和Bernoulli-Euler梁的基本理论给出了框架结构空间动力失稳的理论公式，提出了一种结构空间动力稳定性分析的数值方法。为了验证数值预测，进行了空间自参数内共振和非内共振试验。根据试验与数值计算结果，可以得出以下结论：

(1) 当周期荷载的激励频率约为框架结构空间固有频率的两倍时，框架结构可能由于自参数共振而发生空间动力失稳。

(2) 框架结构体系可以由两个子结构组成。一个子结构是主系统，另一个是次系统。当主系统的固有频率接近次系统的两倍时，主系统的普通共振会引发次系统的自参数内共振。由于普通共振的放大效应，相对较小的激励就可以激发子结构的大振幅自参数内共振，且内共振的不稳定区域比非内共振(正常工况)的不稳定区域大得多。

(3) 数值预测与试验结果吻合较好，说明本文提出的数值方法对框架结构的空间自参数共振研究是有效的。