论如何用小专题复习促进思维生长

庄乐仪

（广东省广州市第十八中学）

一、引言

广东省广州市天河区初中数学研训员刘永东老师曾提出了小专题复习的做法，即以解决一道中等难度的题目为目的，设计以退为进、以小见大、变式迁移和技能训练等四个环节.其中，“以退为进”环节是小专题复习设计的核心，是先将原题“退”到题目中的基本概念或原理（以下统称“题根”），用以触及中等生、学困生的最近发展区，再慢慢呈现题目变化的过程，以一条清晰的主线串联这些概念或原理，“进”到原题中解决问题，凸显以小见大.题根需具有生长性、渗透性，抓住了题根即找到了知识的生长点.因此，小专题复习的设计会直接影响学生解题技能的提升、知识体系的建构和思维的激发.

二、如何开展小专题复习

1.串联知识，完善建构

“以退为进”需将问题退到题根，再由题根按一定的思维主线过渡到原题，这个过程中需设计“了解、理解、掌握”三个层次的题目.其中，“了解”层次的习题从题根出发，以最基本的图形（概念）为背景，设计学生都能独立完成的题目；“理解”层次的习题是题根的初步生长，中等生能独立完成，用以揭示题根本质，有承上启下的作用；“掌握”层次的习题是题根的进一步生长，中等生经教师启发与讨论后能够解决，它的解题方法能用于原题的解决，是最接近原题的习题.三个层次题目的设计层层递进，揭示了知识之间的联系，有助于学生完善自身的知识体系.

案例1：用方程思想解决数轴上的双动点问题.

问题：如图1，已知A，B，C是数轴上三点，点O表示原点，点C表示的数为8，BC=6，AB=14.

图1

（1）写出数轴上点A表示的数为_____，点B表示的数为_____.

（2）动点P，Q分别从点A，C同时出发，点P以每秒4个单位长度的速度沿数轴向右匀速运动，到达原点O立即掉头，按原来的速度运动，点Q以每秒1个单位长度的速度沿数轴向左匀速运动，点P到达点A时P，Q两点都停止运动，设运动时间为t（t＞0）秒.

①当0＜t≤3时，求数轴上点P，Q表示的数（用含t的式子表示）；

②t为何值时，点O为线段PQ的中点.

此题为七年级上学期一道期末考试题.由于学生对数轴上的双动点问题缺少前期的认知，因此解决起来存在一定的难度.此题是一道综合有理数、整式、一元一次方程知识的问题，非常适合用小专题的复习思想将以上知识进行串联，建立知识体系.

热身1：已知，数轴上一点C表示8，若数轴上有一动点Q从点C出发，以每秒1个单位长度的速度沿数轴向原点O匀速运动.设运动时间为t秒，则OQ的长为_______（用含t的表达式表示）.

热身1属于“了解”层次目标，也是问题1的题根之一，要求学生设未知数表示变化的线段长，其中不仅渗透了函数思想，也是解类似问题的必要步骤.学生通过画图体会OQ的长度变化规律，以点O为临界位置，对t的取值范围进行分类讨论，从而求得线段OQ的长不同时段的表达式.

热身2：如图2，点A，C，O在同一数轴上，点O在线段AC上，AO=12，CO=8.若点P从点A出发，以每秒4个单位长度的速度向右匀速运动；同时，点Q从点C出发，以每秒1个单位长度的速度向左匀速运动.当点P到达点C时，P，Q两点都停止运动.设运动时间为t秒，则：

图2

（1）当t为何值时，点P与点Q相遇？

（2）当t为何值时，点O为PQ中点？

（3）当t为何值时，点P与点Q的距离为5？

热身2简化了问题（原题）的运动轨迹，在双动点的相遇问题背景下，设置三个层层递进的小问题，引导学生研究数轴上的双动点问题，逐步接近原题.对于第（1）小题，其中的相遇问题模型符合两点相向运动的背景，学生不难确立等量关系，属于“理解”层次目标，中等生基本能在热身1的基础上独立解决.教师由此可引导学生归纳出题根之二——等量关系的确立.第（2）（3）小题属于“掌握”层次目标，教师要引导学生综合学过的知识确立等量关系解决问题.

以上设问围绕题根设置阶梯式的问题，一步步引导学生把握题根，形成“用字母表示变量—确立等量关系—列方程求解”的思维主线，体现了有理数和整式是一元一次方程的基础，有机地串联了人教版《义务教育教科书·数学》（以下统称“教材”）七年级上册前三章的主要知识点.解决问题不仅要迁移热身1中OQ的长表达式的分类讨论，还要用到热身2中确立等量关系的方法，渗透了分类讨论思想、模型思想、化归思想等.由此可见，以退为进在小专题复习中能串联解题方法和数学思想，完善知识体系的建构.学生的数学思维得到生长后，再经过下一课时的变式迁移和技能训练，数学学习能力也就能逐渐提高.

2.暴露本质，重建模型

“以退为进”要退到题根，再由题根生长出各个层次目标的热身问题.“退”的过程中逐渐暴露出问题的本质，“进”的过程实现对问题模型的重建.下面结合某次九年级下学期期末考试题（案例2）说明如何在以退为进的过程中暴露问题本质.

案例2：解三角形.

问题：如图3，在正方形ABCD中，对角线AC，BD相交于点O，把一块三角板的直角顶点放在点O处，然后绕点O旋转，使得三角板的两直角边分别与AB，BC边交于点E，F.当∠EOB=30°时，测得，求此时正方形的面积.

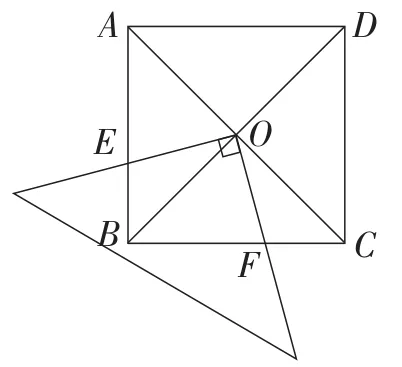
图3

问题中，只要解△OBF求得OB的长，那么正方形ABCD的边长和面积就可迎刃而解.此题的题根就是解含三个已知元素的三角形，“以退为进”环节就是要暴露这一问题本质.虽然九年级学生对解三角形还不熟悉，但对解直角三角形已经比较熟练.以下热身问题就是从这里出发，逐步重建问题模型.

热身1：如图4，在△ABC中，∠C=90°，AB=2，∠B=30°，则AC的长为____，BC的长为_____，S△ABC为____.

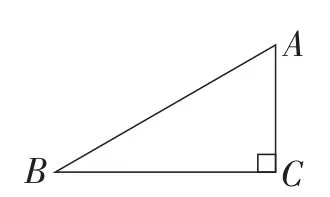
图4

此题属于“了解”层次目标，退到题根——解直角三角形.解三角形的基本方法是构造并解直角三角形，故将热身1的直角三角形一般化，赋予三种具有代表性的条件生成以下“理解”层次目标的热身2，启发学生把握题根、归纳解法——构造直角三角形并求解.

热身2：如图5，已知△ABC.

图5

（1）若AB=2，∠B=30°，∠C=45°，则BC的长为____，S△ABC为____.

（2）若AB=2，∠B=30°，，则AC的长为____.

（3）若AB=5，，BC=7，则S△ABC为____.

热身3：在△ABC中，AB=4，AC=3，∠B=30°，求BC的长.

热身3属于“掌握”层次目标.教师要启发学生自己画图体会图形的分类，更深层次思考问题有利于学生更好地把握解三角形的实质.解决问题也是要先暴露本质，即抽取出模型、解三角形，再回归原图形重建模型、继续求解.教师既要启发学生如何抽取、重建模型，更要归纳、总结在什么情况下抽取模型.明白暴露本质的意义才能突破难点，达到解三角形的应用层次目标.在第2课时，教师可以继续设计如下变式拓展进行技能训练.

变式：如图6，在菱形ABCD中，∠BAD=60°，AB=2，O为边AD的中点，连接CO，求CO的长.

图6

经历了以退为进对模型的抽取与重组以后，学生能更深刻地把握问题实质、体悟如何解题.通过温故知新，再反复进行技能训练，再遇到由此题根生长出的问题时，就能自行抽取模型，暴露题根本质.

3.有效拓展，以小见大

简化原题就要设计在学生最近发展区内的简单题目，以突出核心知识和数学思想的思维训练，即“以小见大”.由此可见，“以小见大”不仅仅是小专题教学设计的一个环节，还是一个内涵更加抽象的理念，对其理解还需要经过不断的教学实践去体验、感知其丰富的内涵.

方程、不等式与函数有着密切的联系，运用转化思想，可以化函数为方程、不等式，也可以构建函数来解决方程、不等式问题.二次函数是初中阶段函数问题的重要组成部分，也是初、高中阶段函数知识衔接的纽带.下面结合一道关于二次函数的代数问题探讨怎样突出“以小见大”的理念.教材九年级上册中已经归纳了二次函数与坐标轴交点个数问题，学生对此的理解也比较深刻，“以退为进”就退到这个最近发展区.具体设计如下.

案例3：二次函数的纯代数压轴问题.

（1）以退为进.

热身1：已知二次函数y=x2-2x-m（其中m＞0），则该函数图象与x轴交点个数为_______.

热身2：求函数y=x2-2x-m（其中m＞0）与图象的交点个数.

热身3：求函数y=x2-2x-m（其中m＞0）与图象的交点个数.

（2）以小见大.

从字面上理解，以小见大是从简单到复杂、从特殊到一般的生长.

首先，线段是有长度、有端点的，是直线的一部分，图形上更加简洁，但条件却更加丰富.线段与抛物线交点个数问题的题根在于先判断线段所在直线与抛物线有无交点.若有，则要判断交点是否在线段上，这就需要结合线段和抛物线的草图来判断；若无，则线段与抛物线无交点.案例3的设计体现了从简单知识点到复杂知识面的生长.简单即小，复杂即大.

其次，案例3经过从含简单参数的二次函数过渡到含复杂参数的需要分类讨论的抛物线；从与坐标轴交点，到与直线交点，再到与线段的交点个数问题的演变，体现了从特殊到一般的认知过程.特殊即小，一般即大.

从更深的含义来看，“以小见大”彰显的是数学核心素养.数学核心素养是学生发展核心素养的数学学科延伸.蔡金法等提出并论述数学核心素养涵盖四种成分：一是数学交流；二是数学建模；三是智能计算思维；四是数学情感.首先，小专题的实施是一个数学交流的过程，“以退为进”环节阶梯式的目标导向，学生之间、师生之间的交流围绕这一环节的习题展开，各层次的学生也能在相应层次习题的交流过程中有所收获.其次，在逐层深入、有序地交流中，教师带领学生挖掘题根，进行数学建模，再将模型应用到解决由题根生长出来的问题.再者，在数学交流中，学生能更好地建构知识体系，达到数学思维的提升，增进交流，增进友谊，教师也能全面地了解学生的思维深度与广度.由此可见，小专题体现的是大素养、大智慧.

三、结束语

由于学情和教学经验不同，不同教师对同一主题小专题的理解各有不同，设计出的小专题也不尽相同，但是这些设计始终离不开削枝强干、化繁为简，其原理都是“退”到题根.把握了题根的本质，就能解决以该题根生长出来的一系列问题.教师先要自己“退”到题根，再用一条脉络串联生长题根，设置阶梯问题，逐步“进”到原题的解决.在小专题的实施过程中，教师要引导学生寻找题根，沿着知识脉络激发学生思维的生长.以小见大，体现在以退为进的过程；以退为进，成就了以小见大的高度.两者有机结合共同构成小专题的灵魂.