强化几何直观教学 发挥数学育人作用——以“一类线段最值问题”的教学为例

曹 宝，饶 黎，周远方

（湖北省武汉经济技术开发区教育局教研室；湖北省武汉市六中位育中学；湖北省教育科学研究院）

《义务教育数学课程标准（2022年版）》明确提出了“增加代数推理，增强几何直观”的主张，体现了借助代数予以表达、通过几何建立直观的现代数学的基本特征.求线段最值（最大值或最小值）问题，既是初中阶段“图形与几何”领域的教学重点，也是学生提升几何直观能力的难点.因此，综合运用几何变化，构造不同折线类型，以单元整体设计的形式开展线段最值问题的专题研究是很有必要的.本文以“一类线段最值问题”的教学为例，通过层层递进和环环相扣的系列化问题展开教学，以期抛砖引玉，引发对该专题内容教学的进一步深入研究.

一、教学内容解析

本节教学内容是在学习了人教版《义务教育教科书·数学》（以下统称“教材”）八年级上册第十三章“轴对称”中的“课题学习 最短路径问题”后进行的，是对应用轴对称变化解决几何问题的巩固和拓展.

轴对称是一种重要的对称，通过对教材中两个典型例题的学习，学生体验了轴对称、平移等变化的运用，可以把已知问题转化成易于解决的问题，从而作出最短路径的选择.整合此前学习的三角形、全等三角形的相关知识，由最短路径问题研究中出现的“定点折线”引出“定长折线”；由轴对称变化发展到平移、构造全等三角形等几何变化；由线段最小值问题过渡到线段最大值问题，可以深化学生在几何图形、几何变化和问题探究等方面的理解.

二、教学目标设置

本节课的教学目标设置如下.

（1）学生能综合运用轴对称、平移、构造全等三角形等变化，解决几何问题.

（2）学生会依托图形进行数学思考，能利用图形猜想可能的结论和论证思路，能运用几何直观进行合情推理，提升逻辑推理能力.

（3）学生经历数学抽象和探究的过程，体会研究几何图形的一般方法，积累数学基本活动经验.

三、学生学情分析

学习轴对称相关知识后，学生已经能够利用轴对称变化研究某些最短路径问题，但有些问题还要借助平移变化、三角形全等等知识进行研究，不同的折线类型会得到不同类型的最值，学生在几何图形认识、几何变化运用和几何问题的转化等方面，其学习活动仍需感性材料的支持.

四、教学策略分析

几何直观与逻辑推理密不可分，它常常依靠逻辑支撑，思索通过看到的图形思考到了什么、想象到了什么.这是数学学习中非常重要而有价值的思维方式.学生运用几何直观把看到的与以前学到的知识结合起来，通过思考、想象，猜想出一些可能的结论和论证思路，这个过程充分利用了合情推理，也为严格证明结论奠定了基础.因此，教师教学中要整合素材、拓宽视野，集趣味性和知识性于一体，兼顾直观形象性与抽象概括性，从而更好地完成教学目标和任务.

本节课尝试以整体关联性为线索，以学生的经验单元、活动单元为基础，打破教材固有的结构，用整体系统的方法对教材中具有关联性的“几何变化、折线、最值”等进行分析、组合、补充，对一类线段最值问题进行统筹和优化，将课堂知识进行迁移，以发展学生的思维，凸显数学的育人作用.

五、教学过程设计

1.以旧引新，揭示问题本质

问题1：如何求两条线段和的最小值？

探究1：如图1，将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的B地开会，应该怎样走才能使路程最短？

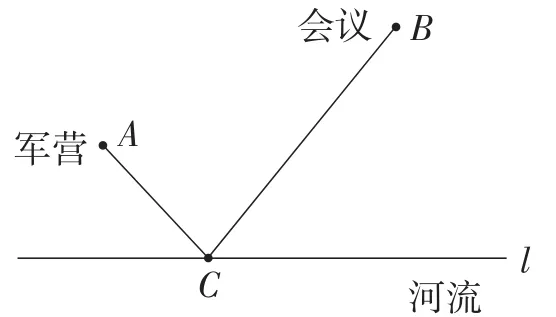
图1

回顾梳理：从回顾学生熟悉的“将军饮马”问题入手，提炼出问题的本质是将实际问题抽象为数学中“两条线段和的最小值”问题（如图2），再利用轴对称的性质将求线段和的最小值问题转化为“两点之间，线段最短”的问题.

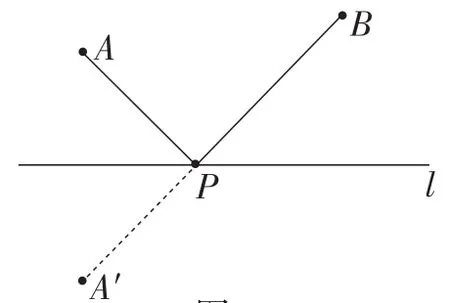
图2

【设计意图】通过回顾这个求线段最值的入门问题，揭示出此类最值问题的数学本质，并理解优化、转化等数学思想方法，起到了推动探究的作用，为一次对称变化过渡到两次对称变化，以及由对称变化引申到其他变化做铺垫.

归纳总结：通过逐步体会并掌握数学思想方法，发展数学核心素养.将实际问题抽象为数学中的求线段和的最小值问题，可以促进学生认识事物的数量、数形关系，掌握数学符号语言，提升数学建模能力.

2.引申拓展，升级求最值

问题2：如何求三段折线和的最小值？

探究2：如图3，∠AOB=30°，M，N分别是射线OA，OB上的点，且OM=1，ON=3，若点P，Q分别是射线OB，OA上的动点，求MP+PQ+QN的最小值.

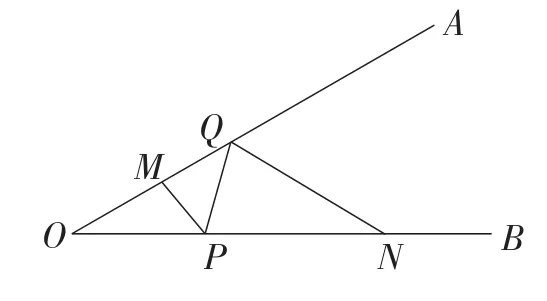
图3

【设计意图】探究2为“将军饮马”问题的升级版，将一条“河”改为两条“河”，需作两次轴对称变化构造出三条线段组成的折线（如图4），其本质依旧是两定点间的折线最小值问题，强化学生对求“定点折线”最小值的理解，让学生感受变化中的不变性.

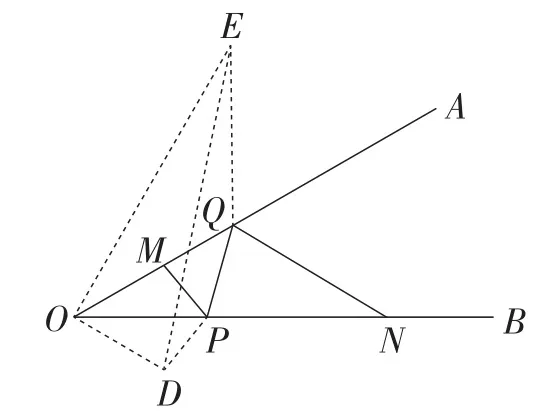
图4

归纳总结：问题虽然升级，但还是属于“两点之间，线段最短”的问题.教师要引导学生运用已有的数学眼光和思维抓住问题的本质，并选择恰当的方法来解决问题，其中，转化思想的运用、判断与选择意识的建立，会促进学生数学核心素养的提升.

3.改变问题背景，引发认知冲突

问题3：如何求两条线段和的最大值？

探究3：如图5，矩形ABCD中，AB=6，AD=8，F为CD的中点，E为矩形外一动点，且∠AEC=90°，则线段EF的最大值为_______.

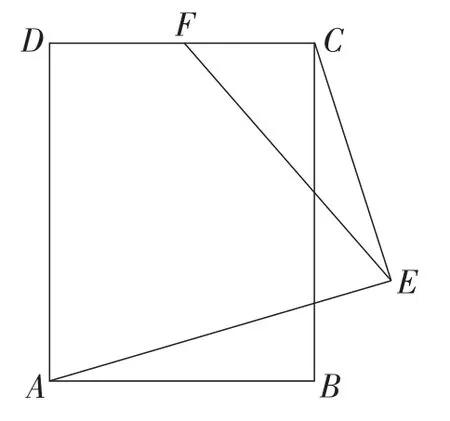
图5

【设计意图】学生发现此题不是“将军饮马”的类型，从而引发认知冲突.教师在启发学生的前提下，引导学生关注定点和定长，并引导他们发现题目中的∠AEC=90°，由此带来了定长，即直角三角形斜边上的中线，随之引出如图6所示的“定长折线”模型.解决探究3后，教师引导学生讨论这道题与探究1和探究2两道题中的折线类型有什么不同，引出“定点折线求最小值，定长折线求最大值”的基本认识.

图6

归纳总结：学生在利用数学知识不断发现问题、提出问题、分析问题和解决问题的过程中，可以产生主动探究的欲望，获得丰富的体验及经验.教师引导学生体验类比、转化思想，可以使学生感受到数学问题解决中曲径通幽、柳暗花明的意境.

4.拾级而上，增添新的元素

问题4：如何利用隐藏对称构造折线求最值？

探究4：如图7，将正方形ABCD沿EF（点F，E分别在边AB，CD上）折叠，点D的对应点G落在边BC上，点A的对应点为点H.若AB=4，则DG+DH的最小值为________.

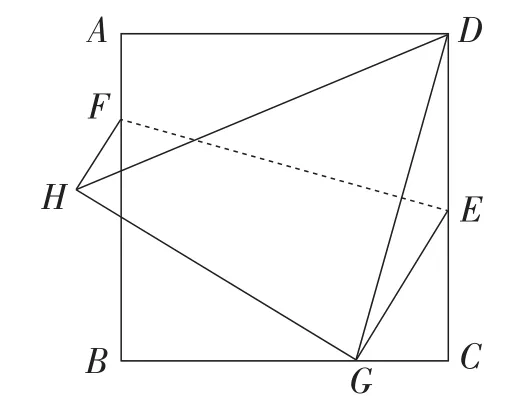
图7

【设计意图】在学生具备基本认识后，探究4给出了四边形经过翻折的情境.在学生探究产生困惑后，教师深入浅出地分析出翻折中隐藏的对称，可得DH=AG（如图8）.一条隐藏的对称实现了线段的等量转换，将难题变成了学生熟悉的“将军饮马”问题，即两定点间的折线段之和问题.

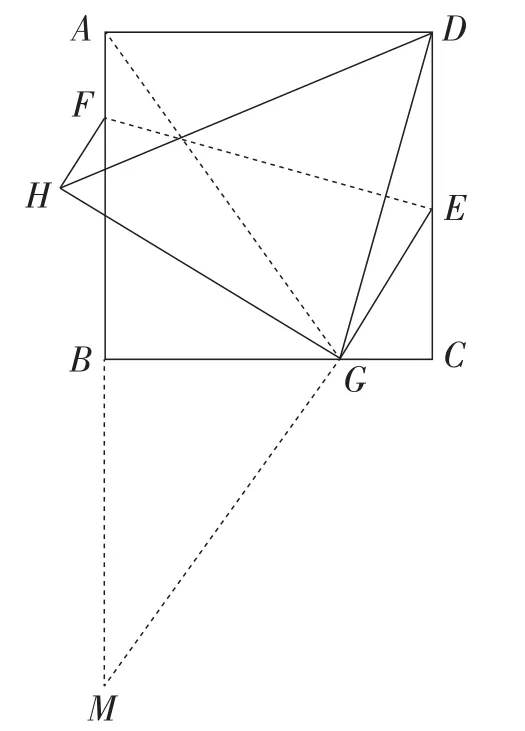
图8

归纳总结：问题一步步升级，学生在不知不觉中拾级而上.教师引导他们通过厘清问题本质，反思、总结方法，深化了对化归思想的理解，发展了合情推理能力和直觉思维，强化了数学思想与方法的渗透，彰显了数学的育人作用.

5.乘胜追击，方法升维升级

问题5：如何利用平移线段构造折线求最值？

探究5：如图9，正方形ABCD的边长为4，O为边AB的中点，正方形ABCD内有一点P，OP=2，E为OP的中点，连接BE，PD，则BE+PD的最小值为____.

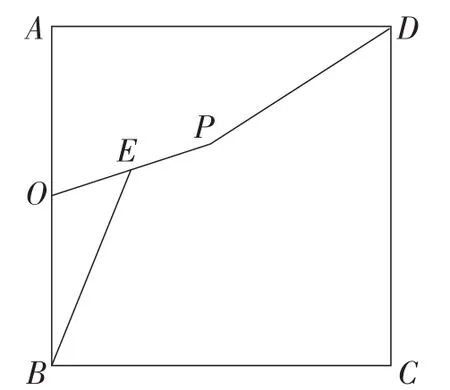
图9

【设计意图】探究5延续了以上的类似背景，在正方形中求被PE隔开的两条线段之和的最小值.为了能培养学生充分的空间想象能力，教师给学生提供了充足的思考时间.在学生尝试对称变化后仍困惑不解之时，教师引领他们另辟蹊径、改变方法.学生发现只需要将BE沿着定长线段EP进行平移（如图10），就可以将被隔开的两条线段BE和PD变成相邻的两条线段，加上定长线段BM，经过平移变化，两段之和转化为三段之和，问题的本质不变，依旧是两定点间的折线段之和最小值问题.

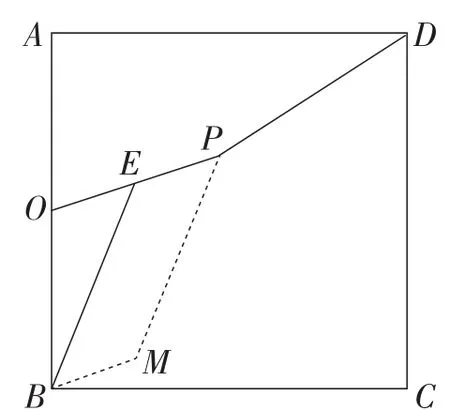
图10

归纳总结：教师先引导学生产生认知冲突，找到方法后再从“形异质同”的题目中归纳出基本模式，体验“多解归一”的策略，既有利于培养学生的整体观念，也能促进学生建立自己的类型题库，在今后遇到同类问题时能快速转化.

6.艰难登顶，一览众山小

问题6：如何利用全等三角形构造折线求最值？

探究6：如图11，∠EAF=90°，B，C分别是射线AE，AF上的两个动点，O是线段BC的中点，线段AO的长始终为1，点M在AB的延长线上，且BM=AC，作∠AMN=45°，交AF于点N，连接ON，则ON的最大值为_______.

图11

【设计意图】学生尝试解决探究6时，发现运用对称和平移都不能解决问题，再次引起学生的困惑，激起他们的探究欲.如图12，通过师生交流，引导学生关注重要的条件BM=AC，可得AB=CN，从而构造△ABO≌△NCP，转移定长线段AO至PN，出现定长折线O-P-N，从而求出ON的最大值.

图12

归纳总结：在此过程中，学生运用数学思想和方法，逐渐形成发现问题和解决问题的策略，体会到数学变化的“威力”，体验到成功的喜悦，深化了对学科价值的理解，发展了数学核心素养.

六、教学反思

1.强化几何直观

良好的几何直观思维有助于理解问题本质，这是数学学习需要具备的重要能力之一.课堂上，教师要带领学生观察、审视几何图形，围绕有价值的问题进行“长时间的思考”，回顾关键条件，引导学生感受解题方向或突破口的获得，理解变与不变，使习题成为学生的“学材”.同时，教师要从解法研究走向教学研究，在实践中不断体会数学学科的育人作用，进一步关注抽象能力、推理能力、几何直观、模型观念等数学核心素养的培养.

2.发挥育人作用

本节课中，通过设计阶梯题目，让学生经历了对称、平移、全等变化，让最值问题显露出本质——定点折线求线段最小值，定长折线求线段最大值.其中渗透了模型思想、构造思想、整体思想；融合了合情推理、归纳推理、演绎推理.教师通过一个个有挑战性问题的解决，引导学生打开思路、悟出本质，展现出相应的思考方式和策略，有利于培养学生主动探究、解决问题的意志品质.

3.抓最近发展区

为了凸显数学育人的作用，教师要找准学生的最近发展区，抓住学生的困惑，为学生提供有适当难度的内容，激发学生的挑战动机，适时点拨，引导学生拾级而上，发挥其潜能，超越其最近发展区而达到下一发展阶段，然后在此基础上进行下一个发展区的发展.

4.培养整体观念

整体性教学的课堂教学模式旨在让学生理解并掌握如何系统地分析问题，以全局的方式去掌握基础知识和基本技能.在数学学习中，知识的结构是非常重要的，这种结构可以帮助学生掌握知识的本质，有助于学生加快学习上的迁移.本节课中，教师尝试设置具有相似度的探究题组成问题群，引导学生发现解题方法上的共性，即均可采用不同方法构造“折线”，化为基本模型.这种结构性的设计，达到了“一线串珠”的效果，让学生体验到“一气呵成”的愉悦.