无速度测量下的航天器安全接近位姿一体化控制
张禹琛,成国瑞,宋申民
(哈尔滨工业大学航天学院,哈尔滨 150001)
0 引 言
作为在轨服务的基本条件,航天器自主交会对接在空间站组装、碎片移除、空间拦截等活动中得到广泛的应用。在实际的对接操作中,航天器会受到飞轮和推进器的同时作用,并同时进行平移运动和旋转运动[1]。此外,为了防止在接近过程中发生碰撞,需要考虑运动过程中的安全约束[2]。因此,在与非合作目标的交会对接任务中,在满足安全约束的同时,实现姿态同步控制和轨道机动控制的位姿一体化避碰控制
目前,在带有安全约束的交会对接问题上,随着理论的深入研究,国内外学者提出了多种控制方法:基于路径规划和凸优化结合的方法[3]逻辑比较简单,但是对计算要求较高,且存在一定的概率寻不到可行解;快速随机树方法、基于随机搜索算法可以找到一条无碰撞方案[4],但是当安全走廊比较狭窄时寻找的时间会大大增加;基于最优控制的方法可以实现燃料最优的安全接近问题[5],然而当动力学模型为强非线性时需要求解复杂的两点边值问题从而确定协态状态的初值;基于混合整数线性规划形式的轨迹规划模型可以在常值小推力模式下实现航天器近距离的安全对接[6],但所应用的C-W方程和T-H方程存在线性化误差,导致对接精度下降;基于人工势函数(APF)的方法可以有效的降低寻找可行解的时间[7],并能实现较高的对接精度,但是APF存在陷入局部最优的情况。
但以上提及的避碰算法仅实现渐近稳定且没有考虑输入饱和对系统稳定性的影响。文献[8-9]基于有限时间控制方法结合APF并使用辅助系统实现航天器位姿一体化对接操作。进一步地,文献[10]基于APF构建编队势场使多航天器保持多边形编队,并实现渐近稳定。考虑执行器故障情况下,文献[11]设计一种三维拼接体作为安全包络区域,并基于APF设计一种容错接近控制律。然而,这些避碰控制策略中采用的安全包络面不是一个封闭的曲面[8],而是使用多个函数的拼接构建包络面[9,11]。为了消除收敛时间对状态初始值的依赖,固定时间控制策略得到学者们的广泛关注,并应用在无人机[12]、航天器姿态控制[13]、制导律设计[14]等领域。但是固定时间控制在航天器位姿一体化交会对接领域的研究成果目前比较少。
在与非合作目标的交会对接任务中由于通常无法直接获得目标航天器的姿态信息和位置信息,文献[15-16]中使用卡尔曼滤波方法确定相对位置和姿态,文献[17-19]中使用基于观测器和自适应技术对目标的非合作特性和模型不确定性造成的影响进行集中补偿,文献[20]使用预设性能控制和反步控制法处理具有安全约束的非合作交会对接问题。由于追踪航天器无法自主获得相对速度和角速度信息,文献[21]采用速度观测器对相对角速度进行估计,实现编队航天器的姿态控制问题;文献[22]直接设计一种不需要角速度信息的容错控制器,实现对柔性航天器的姿态控制。然而,以上方法均不能在目标航天器信息和相对速度信息无法获得的情况下实现高精度位姿一体化控制。因此,同时存在未知扰动、模型不确定性、无法获得速度信息、输入饱和、执行器故障条件时,实现对非合作目标的安全交会对接任务仍然是一个未解决的重要问题。
针对无速度测量情况下的非合作交会对接场景,考虑固定时间控制相比有限时间控制具有快速收敛和高精度等特点,本文使用容积卡尔曼滤波算法(Cubature Kalman filter,CKF)对目标航天器的位置和姿态进行估计,并结合一种固定时间扩张状态观测器(Fixed-time extended state observer,FTESO)设计基于APF的固定时间自适应滑模控制器同时进行位置接近和姿态同步操作。为了同时对执行器故障和输入饱和进行补偿,设计一种非奇异的辅助系统。相比于以往的航天器自主接近控制策略,本文设计算法更加具有实际意义。
1 航天器模型建立
1.1 航天器相对误差动力学模型
本文以与非合作航天器交会对接任务为研究背景,根据刚体动力学和二体问题分别建立追踪航天器与目标航天器之间的相对旋转运动模型和相对平动运动模型。为建立位姿一体化模型,定义坐标系如图1所示。首先定义目标航天器体坐标系Ft(Otxtytzt):Ot为目标航天器质心,xt轴指向对接轴方向;yt轴为目标航天器横向平面与xt轴垂直,向左为正方向;zt轴满足右手定则。追踪航天器体坐标系Fc(Ocxcyczc)建立与Ft类似。

图1 坐标系示意图Fig.1 Coordinate systems diagram
给出目标航天器运动学和动力学模型如下[16]:
(1)
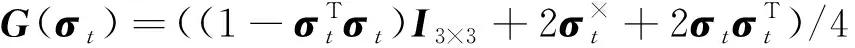
(2)
进而建立追踪航天器的运动学和动力学模型如下:
(3)
式中:τ,f分别为在Fc系下表示的飞轮和推进器输出的控制力矩和控制力;E1,E2表示追踪航天器上的飞轮安装矩阵和推进器安装矩阵。其余的变量定义均与目标航天器的运动模型(1)一致。
定义ρ为期望位置与目标航天器的相对位置矢量,则相对于地心的期望位置rρt和期望速度vρt可表示为:
(4)
定义在Fc系下表示的误差罗德里格参数、角速度误差σe,ωe和相对位置误差、相对速度误差re,ve[23],并得到相对误差运动学和动力学:
(5)
(6)
其中,在Fc系下表示的相对误差动力学中的扰动力和扰动力矩可以写为:
(7)
Ft系转到Fc系的转换矩阵可以表示为
(8)
由于航天器长时间在轨运行的燃料消耗以及载荷变化,追踪航天器的模型参数是不准确的(包括J,mc),此外考虑到执行器存在输入饱和以及执行器故障的情况,相对误差动力学可以进一步推导为:
(9)
(10)
(11)
式中:J0=J-ΔJ,m0=mc-Δm分别为一个正定对角矩阵和正常数;Φ1,Φ2是在相对姿态误差动力学和相对位置误差动力学中模型不确定性造成的影响;d1,d2包括扰动以及由目标航天器的非合作特性引起的未知部分;τc,fc分别表示追踪航天器的飞轮和推进器的实际输出,满足式(12);Ξ1,Ξ2将在之后详细介绍。
(12)
饱和函数sat(u)表示为:
(13)
式中:ui为第i个执行机构,uimax,uimin为第i个执行机构的控制输出的最大值和最小值;追踪航天器飞轮和推进器的健康矩阵可以分别表示为H1=diag(h1,1,h1,2,…,h1,N1),H2=diag(h2,1,h2,2,…,h2,N2),N1,N2分别为飞轮和推进器的数量,h1,i/h2,i分别表示第i个飞轮/推进器的损坏程度:
(14)
通过引入关于ΔJ的线性因子:θ=[ΔJ11,ΔJ12,ΔJ13,ΔJ22,ΔJ23,ΔJ33]T,式(10)~(11)中的Φ1,Φ2可以重写为:

(15)
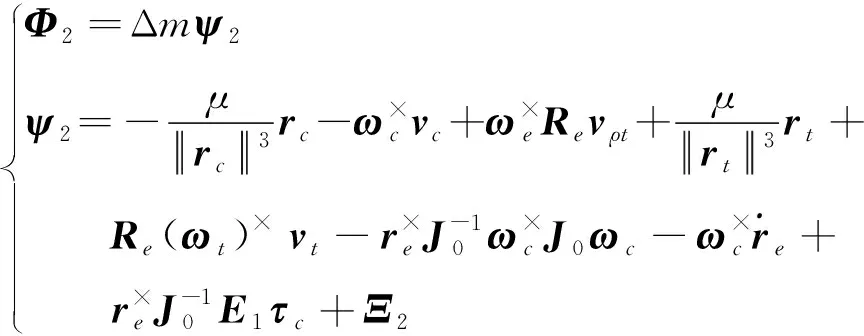
(16)
基于式(12)~(15),式(9)可以重写为:
(17)
由于无法得到目标航天器的准确信息和惯性参数,因此很难得到准确的相对动力学模型。此外,缺少速度测量传感器使得追踪航天器无法获取与目标航天器的相对速度,这也为控制系统的设计造成了很大的困难。本文使用CFK和ESO估计目标航天器的状态和相对速度,将非合作目标转化为半合作目标。
注1.在式(17)中可以看出姿态回路会影响轨道回路:飞轮产生的控制力矩出现在轨道动力学中,即飞轮的输出会影响相对速度的变化。因此本文中推导的位姿一体化模型可以清晰描述耦合关系,并在控制器设计中体现从而提高控制精度。
注2.基于目标航天器的状态初值,使用CFK对量测得到的目标航天器的实时位置和姿态进行估计,并获得更准确的目标航天器状态(rtI,vtI,σt,ωt),其中rtI,vtI表示在地心赤道惯性系下表示的目标航天器的位置和速度。
1.2 容积卡尔曼滤波
本节介绍CFK对目标航天器的状态进行估计:考虑高斯形式的过程噪声w=[w1,w2]T和量测噪声δ=[δ1,δ2]T。得到状态方程和量测方程:

(18)
量测方程:z=[z1,z2,z3,z4,z5,z6]T=
(19)
(20)
式中:Jt,i为目标航天器的惯量主轴方向的惯量。
注3.从式(18)到(20)的转化可以看出,式(20)忽略了非主轴方向的惯量,会造成状态轨迹一定的偏差。然而实际的航天器的主轴方向惯量会远远大于其他方向惯量,式(20)造成的偏差可以当作过程噪声处理,图2为实际的角速度曲线和在姿态动力学中惯量仅考虑主轴方向的近似的角速度曲线对比图。可以看出当整个对接时间在450 s以内时,所造成的角速度偏差较小可以当作扰动处理。
定义状态量为X1=[σt,ωt,λt]T,X2=[rtI,vtI]T,将状态方程重新写为:
(21)
式中:W=λ·ωt。

图2 角速度对比图Fig.2 Angular velocity comparison
基于CFK的目标航天器轨道状态和姿态状态估计算法如下所示[24]:
1)初始化
X(0)=X0,P(0)=P0
(22)
2)时间更新
计算k-1时刻容积点:
(23)
式中:Sk-1由Pk-1|k-1的Cholesky分解得到。定义n为状态的维度,点集ξi及权值wi定义为
(24)
计算一步预测值和方差:
(25)
式中:f(·)为式(21)描述的状态方程;Qk为过程噪声方差矩阵。
3)量测更新
计算量测更新的容积点
(26)
(27)
式中:h(·)表示式(19)描述的量测方程。计算增益矩阵:
(28)
式中:Rk为量测噪声方差矩阵。
计算状态估计值和误差协方差:
(29)
基于CFK可以通过仅量测目标航天器的位置和姿态准确估计目标航天器的速度和角速度,并将原来与非合作目标的交会对接任务转变为半合作交会对接任务。估计误差在之后的环节以扰动形式出现在动力学中,并在控制器设计中进行补偿。
1.3 人工势函数
为了实现存在运动约束情况下的交会对接任务,需要在追踪航天器的行进轨迹上设定一个与目标航天器固定的禁飞区域,当追踪航天器一直保持在这一区域外部时,可以保证追踪航天器不会与目标航天器发生碰撞。
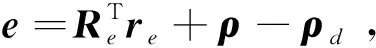
(30)
式中:
包络面是一个封闭曲面,具有如下几种性质:
(1)光滑且连续;
(2)可以通过安全走廊让追踪航天器到达目标航天器的对接口。
相比其他文献中设计的安全包络面,本文设计的包络函数仅由一个函数构成且在控制器设计中能保证避碰函数h导数连续,有效地减少了控制器的抖振现象。为了清晰展示所设计的包络面的大小,当h=0时,绘出三维包络图,如图3所示。
注4.文献[9,11]提出的拼接曲面表达式为:
(31)
式中:b3≥a3≥a2≥a1>0。当对拼接曲面函数求导时,在其拼接处对相对位置e的偏导数不连续,导致在e1穿过a1,a2时,控制器的输出产生突变。而本文所设计三维包络面(30)仅由一个光滑函数构成,因此可以保证导数连续,产生的控制输出更加平滑。
两种三维包络面的二维投影如图4所示,可以看出本文所设计的包络面更加平滑;通过设计一条安全接近走廊保证追踪航天器在不与目标航天器发生碰撞的前提下完成交会对接任务。
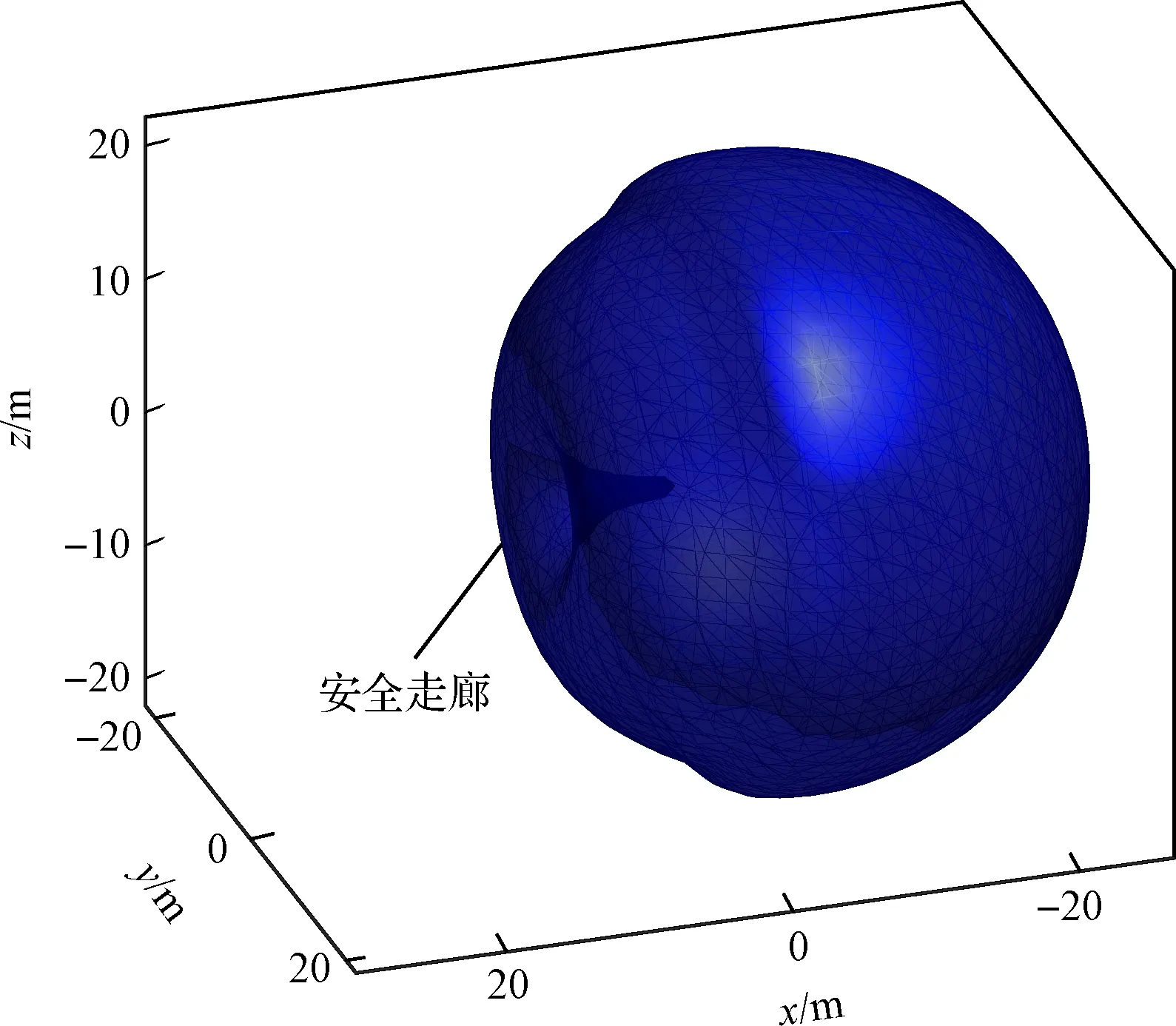
图3 三维包络面示意图Fig.3 3D envelope surface
基于式(30)构成的安全包络函数,设计一种人工势函数如下:
(32)
式中:ky1,ky2为正常数。当h(e)大于零时,可以保证追踪航天器一直处于包络面外部,此时设计的势函数Y也是有界的。
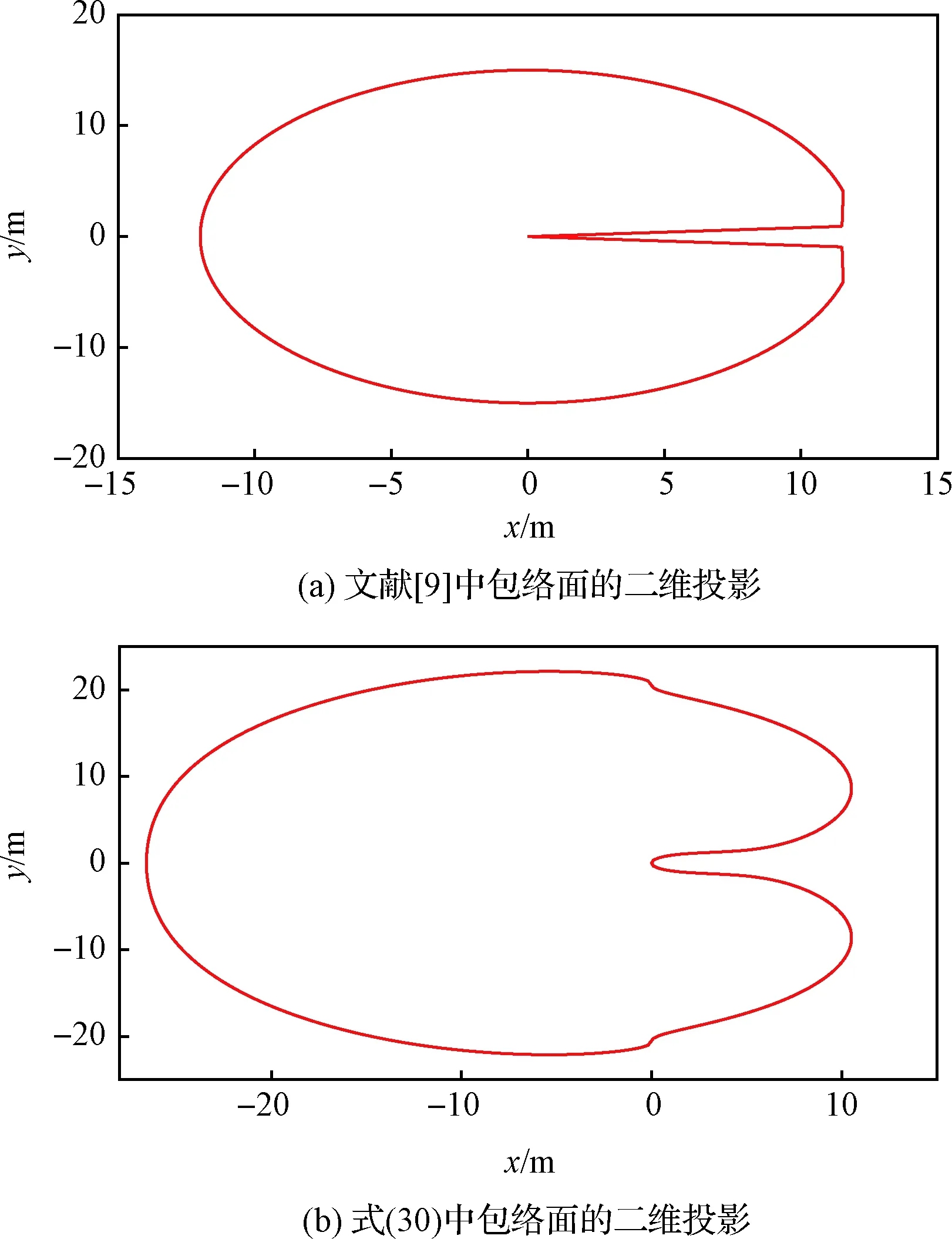
图4 两种包络面的二维投影对比图Fig.4 Two-dimensional projection comparison of two envelope surfaces
2 控制器设计
根据考虑耦合的相对误差动力学式(17)和CFK算法式(22)~(29),并在所设计的人工势函数式(32)基础上,设计一种基于扩张状态观测器的固定时间滑模控制器。该控制器可以保证追踪航天器在同时出现输入饱和、执行器故障情况下仍可以安全地完成非合作交会对接任务。
2.1 相关引理和假设
为进行控制器设计,先提出一些引理和假设。
引理1.对于任意的常数a满足如下不等式:
(33)
式中:ε是一个正常数。
引理2[25].对于系统y=f(x),如果存在一个李雅普诺夫方程V(x)和正常数α>1,0<β<1满足如下方程,则该系统是实际固定时间稳定的且状态x可以在时间tmax之后收敛到边界φx内部。
(34)
且收敛时间为tmax=1/(c1(α-1))+1/(c2(1-β)),收敛边界为
φx=
式中:c1,c2>0;θ∈(0,1);Ω是有界的。
引理3[25].对于任意的正常数α>1, 0<β<1以及向量x∈N,满足如下的不等式:
(35)
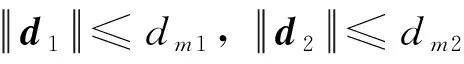
假设2.追踪航天器仅能观测到与目标航天器的相对位置和相对姿态,无法获得相对速度和相对角速度。
假设3.追踪航天器的起始位置和期望位置均处于安全包络面外部。
假设4.执行器发生故障之后仍满足rank(E1H1)=rank(E2H2)=3。
注5.由于航天器的惯性参数、控制幅值和系统的外部扰动都是有界的,因此假设1合理;考虑到追踪航天器体积较小,仅安装激光测距传感器和相机,因此假设2合理;为了实现安全交会对接任务,需要保证追踪航天器距离目标航天器一定范围开始机动且对接成功之后不会发生碰撞,因此假设3合理;由于欠驱动系统不属于本文的研究范围,因此假设4也是合理的。
2.2 固定时间扩张状态观测器
由于追踪航天器不能直接得到与目标航天器的相对速度,本节介绍一种固定时间扩张状态观测器,可以在固定时间内准确估计相对速度和相对角速度:
首先将模型(17)重写为:
(36)
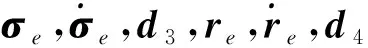
(37)
式中:cij(i=1,2,…,6;j=1,2)为正常数;对于任意的x∈3,定义如下函数:sigγ(x)=diag()sgn(x);αi=i(α-1)+1,βi=β+(i-1)(1/β-1),α∈(2/3,1),β=1/α,i=1,2,3。
通过应用如上的观测器,可以保证在固定时间T0内η1,η2,η3,η4,η5,η6均能收敛到真值附近。且存在正常数σ,r满足r。为了简洁,观测器(37)的收敛性证明参考文献[26]。
注6.通过CFK算法可以获得滤波之后的目标航天器在地心赤道系下的位置rtI、速度vtI以及自身的姿态σt和角速度ωt。结合ESO(36)输出状态和式(5)可以得到估计的rc,vc,σc,ωc。进而可以获得式(17)中的Nω和Nv。其中CFK的估计误差可以被合并进动力学的扰动项d1,d2中。
2.3 固定时间姿态控制器设计
为了实现固定时间姿态同步,设计一种非奇异姿态滑模面S1如下:
(38)
式中:
f(σe,i)=

(39)
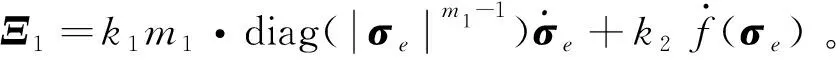
(40)
(41)
因此,所设计的固定时间滑模面是光滑的且不存在奇异问题。在接近原点时,状态量收敛的速度仅仅与ε1有关,通过调节更小的ε1能实现σe更快的收敛。

为了使追踪航天器在输入饱和、模型不确定性、存在扰动和执行器故障情况下仍可以在固定时间内实现与目标航天器的姿态同步,基于滑模面(38),一种自适应固定时间抗饱和姿态控制器设计如下:
(42)
(43)
(44)
(45)
(46)


定理1.在同时存在输入饱和、执行器故障、模型不确定性以及外界扰动的情况下,采用式(37)表示的滑模面,并在姿态控制器(42)、自适应方程(44)~(45)和辅助系统(46)的作用下,系统的滑模面S1和系统状态σe,ωe可以在固定时间T1内分别收敛至原点邻域φs1,φσ,φω。
证.设计一个李雅普诺夫函数如下:
(47)
对上式求导并代入控制器(42)和辅助系统(46)得到:
(48)
将自适应方程(44)~(45)代入上式得:
dm1κ1≤-a1Vσ1+b1
(49)

(50)
式中:
因此,根据以上分析可知b2是有界的,基于引理2可得Vσ2是实际固定时间稳定的,因此S1可在固定时间t1=2/(a2(c1-1))+2/(a3(1-c2))内收敛至边界φs1:
式中:0<ζ<1;λmax(J)表示J的最大特征值。当滑模面S1收敛至φs1后,相对状态σe,ωe随着在S1上滑动至各自的边界φσ,φω。
(51)

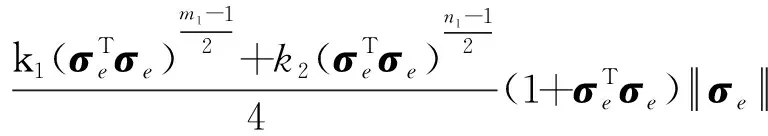
(52)
上式可以写成如下两种形式:
(53)
(54)
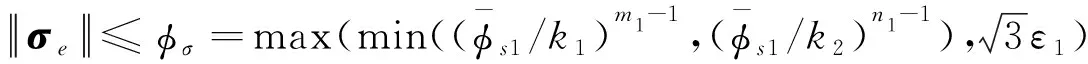
基于以上分析可知在时间T1=t1+t2内,相对姿态σe和相对角速度ωe可以在模型不确定性和外界扰动存在时分别收敛至φσ和φω。
2.4 固定时间轨道控制器设计
为了实现固定时间内满足安全约束条件下实现自主对接,结合人工势函数式(32)设计滑模面S2如下:
(k3sigm2(re)+k4g(re))
(55)
式中:

对式(55)求导得:
(56)
式中:
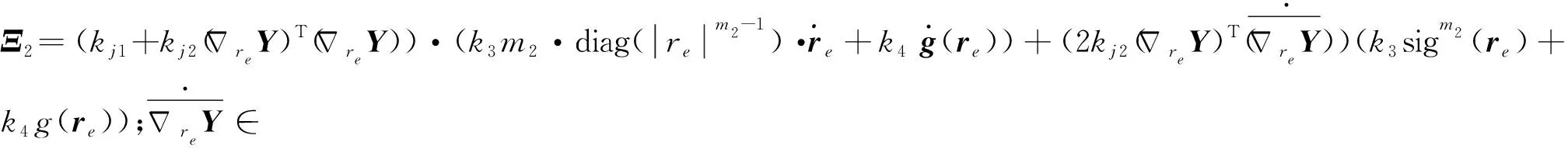



为了使追踪航天器在输入饱和、模型不确定性、存在扰动和执行器故障情况下,并满足安全约束条件下实现自主对接,基于滑模面(55),一种自适应固定时间抗饱和轨道控制器设计如下:
(57)
(58)
(59)
(60)
(61)

注11.由于相对角速度ωe和姿态控制器(42)存在于轨道控制器(57)中,因此设计轨道控制器时会受到姿态控制器的耦合影响。为了减少设计难度并解决存在约束问题,本文分别设计姿态控制器和轨道控制器并实现姿轨一体化的协调控制。
证.设计一个李雅普诺夫函数如下:
(62)
对上式求导并代入式(57)~(61)中得到:
(63)
进一步推导得:
dm2κ2≤-a4Vr1+b3
(64)

(65)
式中:
a5=2(1-c3)/2min(3(1-c3)/2ks3(2/mc)(1+c3)/2,
因此,根据以上分析可知b4是有界的,基于引理2可得Vr2是实际固定时间稳定的,因此S2可在固定时间t3=2/(a5(c3-1))+2/(a6(1-c4))内收敛至边界φs2:
φs2=
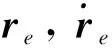
(66)
上式可以写成两种形式:
(67)
(68)

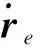
注12.在本文设计的固定时间抗饱和控制器作用下,追踪航天器与目标航天器的相对姿态和相对位置的收敛过程可以分别保证在T1,T2内完成。且收敛时间仅仅受到控制参数的影响而与系统状态初值无关。
3 仿真校验
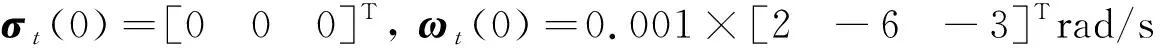

mt=5426.6 kg,

表1 目标航天器初始时刻轨道根数Table 1 Initial orbital elements of the target spacecraft
设计参数中m0=60 kg,J0=diag([30,40,30])。目标航天器和追踪航天器受到的扰动力矩和扰动力被考虑是相同的:
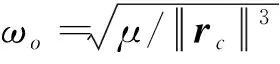



表2 执行器工作情况Table 2 Working conditions of the actuator

图5 姿态误差Fig.5 Attitude errors
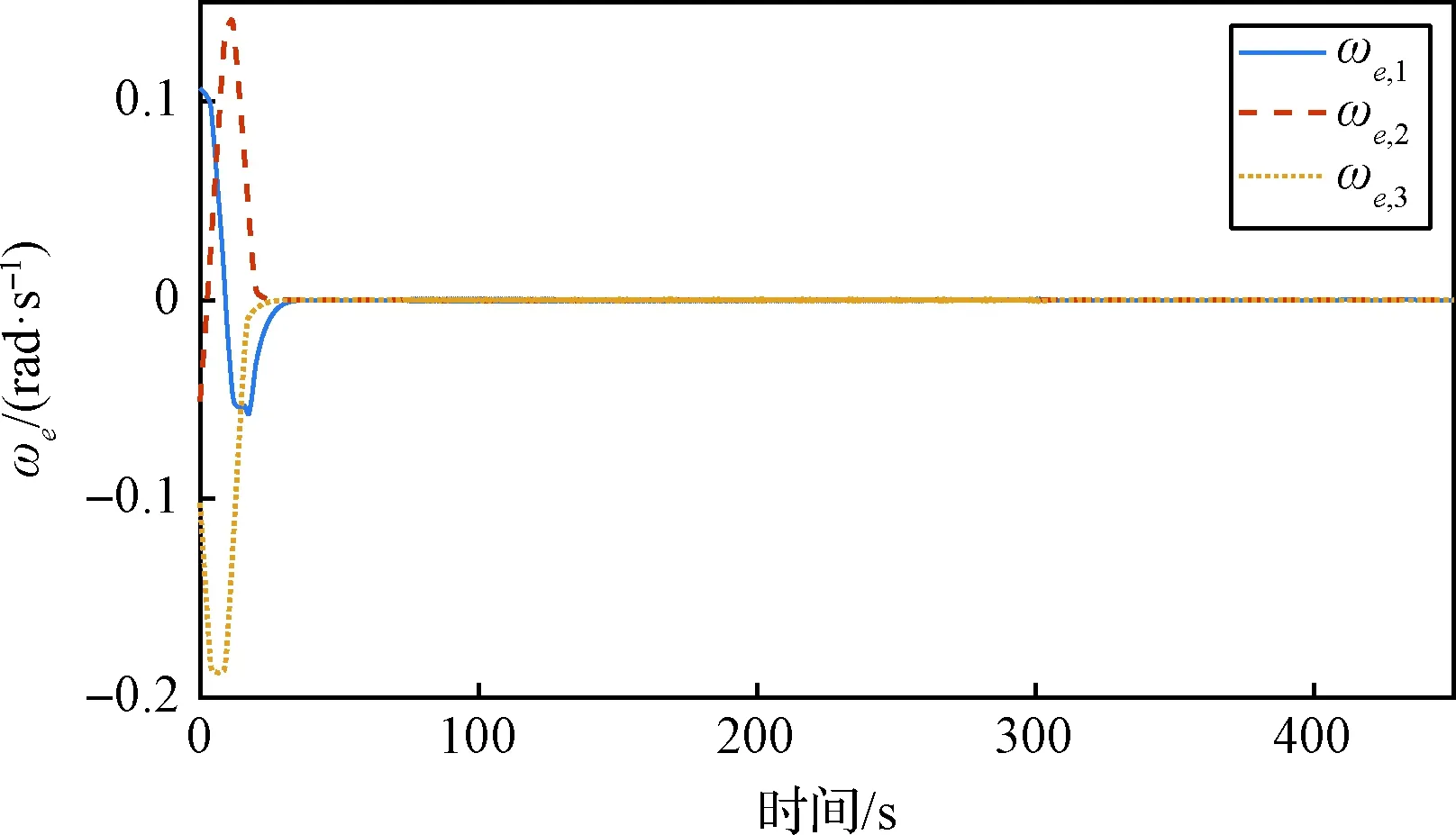
图6 角速度误差Fig.6 Angular velocity errors

图7 相对位置误差Fig.7 Relative position errors

图9 h变化曲线Fig.9 Curve of h

图10 控制器输出Fig.10 Output of the controller
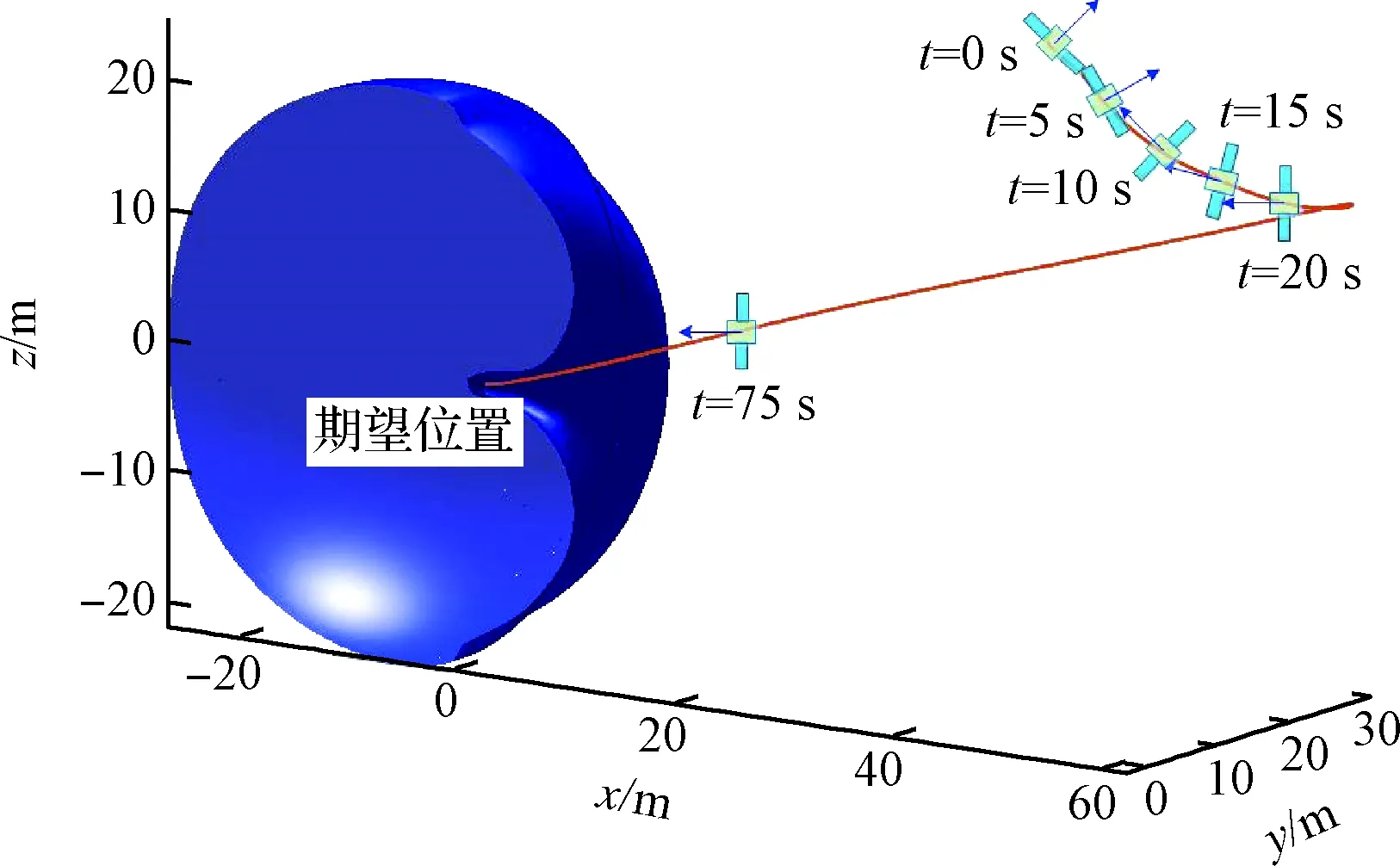
图11 三维轨迹图Fig.11 3D trajectory diagram
4 结 论
本文设计一种固定时间控制策略来解决同时存在运动约束、输入饱和、执行器故障情况下的六自由度非合作交会对接问题。首先,使用容积卡尔曼滤波估计非合作目标航天器的状态,并设计一种光滑的三维闭合曲面作为目标航天器的安全包络面。之后,基于扩张状态观测器和人工势函数设计位姿一体化自适应避碰固定时间滑模控制器。同时,设计一种非奇异辅助系统对执行器故障和输入饱和造成的影响同时进行补偿。最后,使用李雅普诺夫方法证明了最终的收敛时间与状态初始值无关。仿真结果表明了所提控制策略的有效性。未来的工作将致力于使用强化学习方法解决无速度情况下的非合作交会对接问题以获得更好的控制效果。

