利用姿态机动的绳系卫星编队系统轨道协同控制
贾 程,孟中杰
(1. 西北工业大学航天学院,西安 710072; 2. 西北工业大学航天飞行动力学重点实验室,西安 710072)
0 引 言
航天器编队具有系统成本低、工作性能好、可靠性高等优点,在通信、导航、对地观测等航天领域中存在巨大的发挥空间,并展现出非常广泛的应用前景[1]。针对编队航天器的构型维持、轨道机动[2]、碰撞规避[3]等问题,已有相当可观的研究成果。
由于系绳特有的柔性和弹性,绳系系统在轨运行过程中会显现出特有的一些动力学现象,对于绳系卫星的编队控制,目前仍有许多急需解决的问题。以系绳摆动为例,在机动变轨过程中,系绳并不能严格与推力方向保持一致,会导致系绳产生周期性的摆动现象[4]。系绳摆动会产生张力力矩作用于领航星,干扰其姿态甚至影响整个绳系编队系统的轨道运动。因此,系绳摆动的抑制问题得到了广泛关注。
受科氏力影响,通过合理地收放系绳可以实现系绳摆动的抑制,基于此,Vafamand[5]提出了一种鲁棒自适应反步控制器调节绳长以抑制摆动,并采用径向基函数(Radial basis function, RBF)估计系统的未建模动态和不确定性。Liu等[6]在得到能抑制摆动的期望绳长速率后,根据小增益理论设计了张力控制律,从而实现绳长和速率的跟踪控制。Wen等[7]通过势能成型和阻尼注入理论,提出了仅利用绳长反馈信息的张力控制律。刘贺龙等[8]基于高阶滑模算法设计了无抖振的系绳张力控制律,在保证高精度跟踪的同时,有效避免了滑模控制固有的抖振现象。通过收放系绳抑制摆动具有两个问题导致其适用范围受限,一是需针对重力梯度较大的低轨卫星才能显著抑制其摆动;二是频繁地收放系绳必然会导致系绳张力的突变,引发绳系卫星所特有的松弛等现象,严重时甚至会引起编队卫星之间的碰撞[9]。卢山等[10]以拖船航天器喷气推力为控制器输入,基于相平面方法设计了组合体的面内外摆角控制律,并将摆角衰减至稳定极限环内,但并未完全消除摆动现象。Yousefian等[11]通过分析卫星姿态与系绳摆动间的动力学耦合特性,提出利用姿态机动抑制系绳的控制方法。但在他们的研究成果中,摆动抑制耗时长达多个轨道周期。在此基础上,Meng等[12]在卫星推力作用下基于卫星姿态机动设计了能实现系绳摆动抑制的分层滑模-预测控制算法,使平台能跟踪标称轨道且同时抑制系绳摆动。但是,上述文献均忽略了系绳的摆动对卫星轨道的干扰。根据文献[13],摆动会影响领航星姿态,改变平台推力进而导致系统偏离预定轨道。因此,在轨道机动过程中,除抑制系绳摆动外,还需要使系统轨道跟踪其参考指令值,以实现精确的轨道转移。
由于滑模控制具有算法简单、对匹配扰动和模型不确定项具有鲁棒性等优点,并在航天器的姿轨控制方面有广泛应用[14-15],故本文亦采用滑模控制算法改变领航星推力方向以实现轨道跟踪与摆动抑制,并考虑了系绳摆动对领航星轨道的影响。此外,结合模型预测控制(Model predictive control, MPC)算法设计滑动模态的切换控制输入,以尽量降低抖振的影响。
本文后续章节安排如下:第2节基于拉格朗日法建立了绳系系统的面内运动模型;第3节以推力方向角作为控制输入,基于分层滑模控制(Hierarchical sliding mode control, HSMC)和MPC算法设计了相应的控制算法;第4节采用MATLAB/Simulink平台搭建了相应的数字仿真平台并验证了所提控制算法的有效性;第5节给出了相应结论。
1 绳系双星编队系统模型
绳系双星编队系统平面模型如图1所示。其中r为领航星质心的轨道地心距,α为领航星纬度幅角,γ为领航星推力方向角,d为领航星与追随星之间的质心距,θ为系绳面内摆角。

图1 绳系双星编队系统模型示意图Fig.1 Model of the tethered two-satellite formation system
绳系双星编队系统的运动方程由领航星质心的轨道运动方程和追随星相对于领航星的运动方程两部分组成,分别如式(1)和式(2)所示[16]。
(1)
(2)
式中:mp,md,mt依次为领航星、追随星和系绳质量;m=mp+md+mt为耦合体系统总质量;m*=(mp+mt/2)(md+mt/2)/m-mt/6为系统约化质量;F为领航星推力;γ为推力方向角,可通过领航星姿态机动改变。广义力、力矩和Qd,Qθ分别为:
(3)
式中:T为系绳张力。
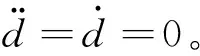
(4)
至此,式(1)~(4)共同组成绳系拖曳系统的平面模型如下:

(5)

由式(5)可以看出,摆动抑制与轨道跟踪都可通过姿态机动调整推力方向角来完成。考虑到领航星具有完备的姿态控制功能,且已有相当文献对其进行研究,本文并不涉及领航星姿态控制。此外,面内摆动系统共有3个自由度,控制量却只有推力方向角γ,又因为推力方向角γ与状态矢量互相耦合,属于典型的非仿射欠驱动控制问题。
2 控制器设计
2.1 领航星质心参考指令设计

(6)

基于以上摆动平衡位置和参考领航星轨迹,可得如下控制目标:
(7)
2.2 控制算法设计
由上一节分析可知,由领航星姿态机动调整推力方向角实现系绳摆动抑制和轨道跟踪的控制策略导致整个系统是非仿射欠驱动系统。因此,本节通过辅助积分法[18],将姿态角速度视为虚拟控制量,把原系统转化为仿射型,在此角速度驱动下,领航星能抑制系绳摆动且能跟踪期望轨迹。具体来说,以各状态变量作为反馈信号,使用二阶HSMC算法和基于超螺旋算法(Super-twisting algorithm, STA)的控制观测器,推导得到角速度在滑动模态上运动的等效控制律,并结合MPC算法给出了趋近控制律。相应的控制结构图如图2所示。
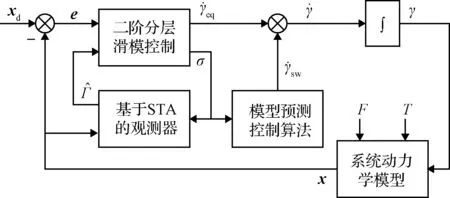
图2 编队系统控制结构图Fig.2 Control diagram of the formation system
由图2可知,控制系统包括二阶HSMC算法,基于STA算法的控制观测器和MPC算法三部分。下面分别进行介绍。
1)分层滑模面设计
首先,定义跟踪误差向量为
e=x-xref
(8)
式中:xref为式(7)给出的参考指令。对式(8)求导,得到
(9)
式中:
(10)
将误差系统(9)划分为三个子系统,并分别设计对应的滑模面为:
si=kie2i-1+e2i
(11)
式中:ki为待定正系数。
定义聚合型分层滑模变量如下:
(12)
式中:k4和k5为待定权重系数。
2)基于升阶法的等效控制律设计

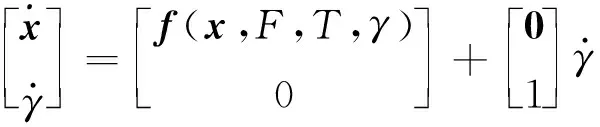
(13)

(14)
式中:
(15)
设计最高层滑模变量为:
σ=k6S+Sv
(16)
式中:k6为最高层滑模变量的待定权重系数。
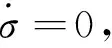
(17)

3)基于STA算法的控制观测器设计
考虑到Γ的真实值难以获取,故采用基于STA算法的控制观测器对其进行估计。定义观测误差为:
ξ=-σ
(18)
(19)
将式(19)代入式(18)的一阶导数中可得:

(20)
(21)
式中:k7和k8为待定正系数。
4)基于MPC算法的趋近律设计
典型的滑模控制算法可分为趋近控制律和等效控制律两部分。其中等效控制律已由式(17)得到,本小节结合MPC技术计算得到切换控制输入项使得滑动模态以最优的方式趋近于滑模面,以克服抖振影响。
MPC的控制目标为使最高层滑模面σ趋于0,即σ→0。令采样时间为Ts,采用一阶欧拉法将系统(16)离散化为:
(22)
基于预测模型(22),可迭代计算得到预测时域Np内的状态变量σ(k+i+1k)(i=0,1,2,…,Np-1),定义二次型性能指标函数为:
(23)
式中:Q,R为正定权重系数。


(24)
因此,在k时刻,MPC控制问题可描述为:
(25)
求解上述优化问题,然后将优化解的第一个分量uk|k作用于系统,循环往复至k→∞。
在控制律(25)作用下,被控系统是渐近稳定的。仿照文献[19-20],证明过程如下。
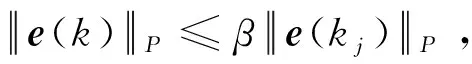
(26)
式中:e(0)为初始误差值。
由ρ∈[0, 1)可得eρ-1-ρ≥0与ρk≤e-(1-ρ)k等价,因此可得
(27)
和
(28)
注意到int(k/N)≥(k/N)-1,故
βe-(1-ρ)int(k/N)≤βe-(1-ρ)[(k/N)-1]
(29)
因此,对任意k∈Ζ+都有
(30)
即系统是稳定的。证毕。
3 仿真校验
为验证控制策略的有效性,采用MATLAB/Simulink搭建仿真平台。拖曳系统参数如表1所示,控制器参数如表2所示。同时,考虑到领航星推力方向改变是由姿态机动实现的,而姿态机动过程中,其角速度不能太大以防止引起挠性附件振动等,因此推力方向角和角速度的变化范围分别取为[-π/9, π/9]和[-0.1, 0.1]rad·s-1,并取仿真时长为200 s,步长为0.1 s。同时,取文献[10]中所提出的双闭环分层滑模/模型预测方法作为对比,仿真结果如图3~6所示。

表1 编队系统参数Table 1 Parameters of the formation system
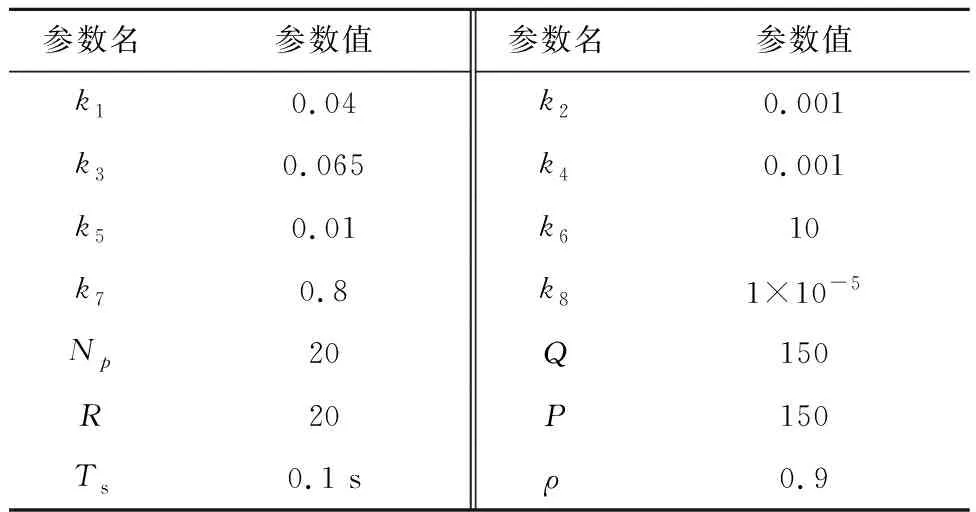
表2 控制器参数Table 2 Parameters of the controller
图3为系绳面内摆角在轨道机动过程中的变化曲线。可以看出,面内摆角在150 s后便能跟踪上平衡位置,且整个跟踪过程较为平稳,超调角度约为16.1°,表明系绳“摆动”在所设计的控制算法作用下可以得到完全抑制。

图3 面内摆角及其导数跟踪轨迹Fig.3 Trajectory of the in-plane angle and its derivative
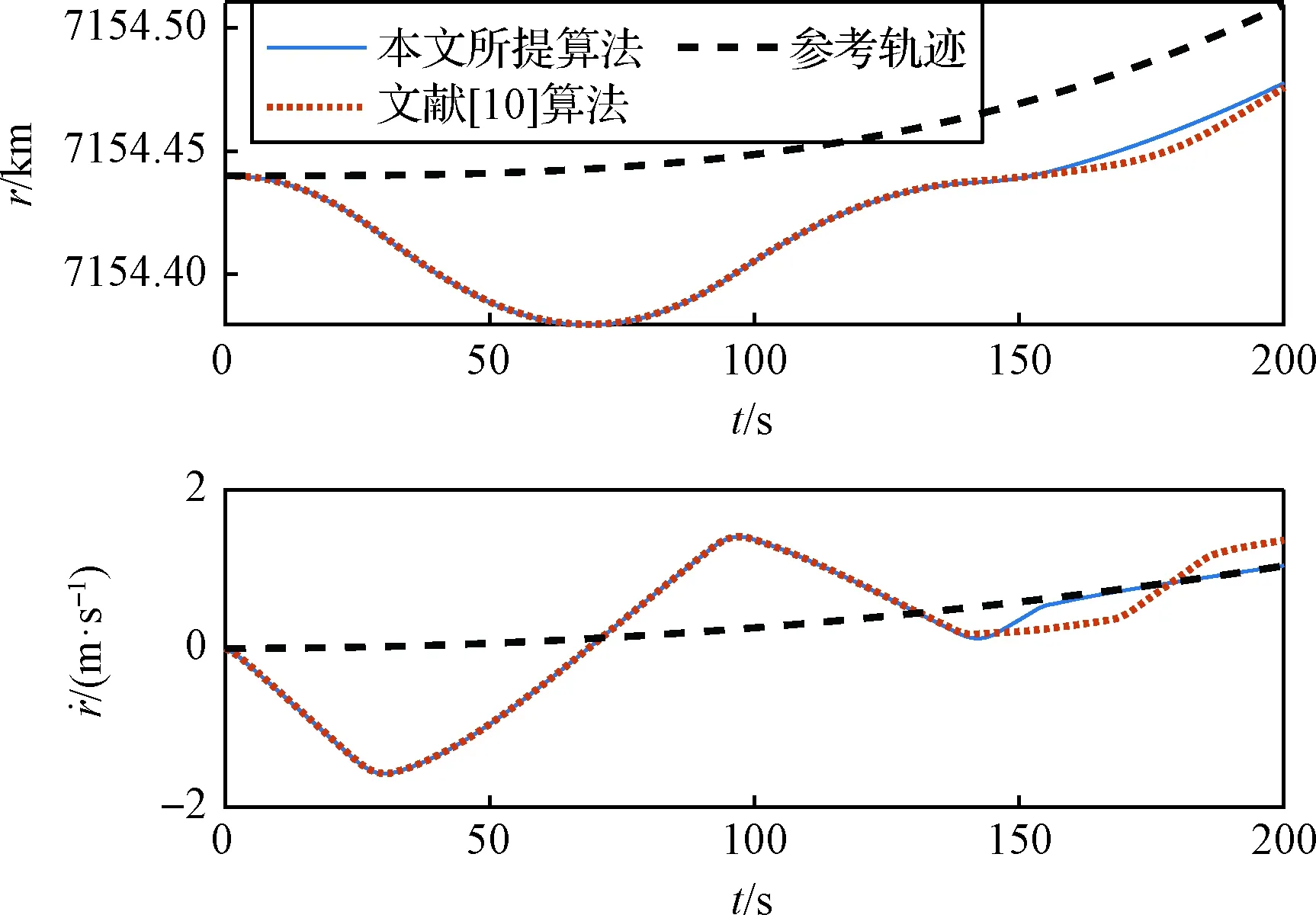
图4 地心距及其导数跟踪轨迹Fig.4 Trajectory of the radius and its derivative
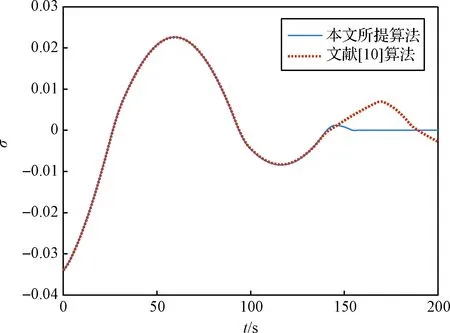
图5 最高层滑模量变化曲线Fig.5 Trajectory of the highest layer sliding variable
图4为轨道机动过程中领航星的轨道地心距的变化曲线。可以看出,在机动过程的初始阶段,面内摆角的存在使得推力方向与编队系统并不严格共线,此时在领航星推力作用下,轨道地心距跟踪误差逐渐增大;约70 s后,地心距变化率超过其参考值并逐渐逼近于参考值,跟踪误差逐步减小,可以预见,经过一定时间,便可以实现轨道地心距的精确跟踪。
图5给出了最高层滑模变量σ的变化曲线,推力方向角及其角速度绘制于图6中。在系绳摆角趋于稳定后,最高层滑模面逐渐收敛到0,与文献[10]中推力方向角在0附近来回波动不同,本文所设计的基于模型预测的滑模趋近律可以使角度平滑地收敛到0附近,且整个控制过程中大大削弱了角速度的抖振现象。此外,本文所提算法在整个控制周期内均没有违背角度和角速度的约束条件。

图6 推力方向角及其导数变化曲线Fig.6 Trajectory of the thrust direction and its derivative
需要指出的是,在控制初期,两种控制算法表现出了极其相似的运动行为。分析可知,系统的动力学行为主要由推力大小所决定,为将摆角快速收敛到参考指令附近,控制初期推力方向角始终保持在其边界值附近,相近的变轨推力必然会导致相似的运动行为。但随着时间的推移,推力方向角逐渐衰减至0,系绳摆动对系统的影响愈发明显。由于本文直接考虑了其影响,因此,面内摆角和地心距的收敛速度有所提升。
4 结 论
针对绳系编队系统的轨道协同机动控制问题,本文提出一种通过调整领航星推力方向进而实现编队系统轨道机动的控制算法。具体来说,在采用拉格朗日法建立双星系统的数学模型之后,对其进行适当简化以便于控制器设计;其次,分析系统的平衡位置并设计了相应的参考轨迹;在此基础上,为各子系统设计相应滑模面后将其聚合得到高层滑模面和等效控制输入;为解决控制策略导致的非仿射问题,采用升阶法将角速度作为虚拟控制输入并采用观测器在线估计系统的非线性项;然后基于模型预测控制算法实现最高层滑模面的趋近控制;最后采用MATLAB/Simulink验证了所提算法的有效性。

