基于Backstepping的非线性无人船航向控制算法

魏 琼， 周 刚， 金 鹏， 张金姣， 胡新宇

(湖北工业大学机械工程学院， 湖北 武汉 430068)

无人船在海洋航行时受到风、浪、流的影响，出现轨迹偏离的情况，因此一个具有抗干扰能力的航向控制器是至关重要的[1]。目前，无人船航向控制算法主要有传统PID、模糊PID自适应控制、神经网络控制和其他一些基于专家经验智能算法的结合算法等[2]。但是这些算法与无人船航向控制器的设计结合时大都采用Nomoto线性无人船模型[3]。由于无人船装载状态、外界干扰等时常发生变化，线性模型已经不能精确描述系统的动态响应特性[4]。针对上述问题，本文在具有非线性特性的船舶运动模型中考虑了相关参数和外部干扰的不确定性，设计了非线性Backstepping自适应控制算法，并使用Lyapunov函数进性论证，仿真验证该算法合理可行。

1 无人船和干扰模型设计

由于无人船装载状态、外界干扰等时常发生变化，仅线性无人船Nomoto模型已经不能准确地描述系统的动态响应特性，所以应采用无人船非线性Norrbin模型。

1.1 无人船模型设计

Norrbin模型[5]可表示为：

(1)

(2)

其中，θ1=-1/T，θ2=-α/T，b=K/T。假设外界干扰是有界的[7-8]，因此|ω|≤Φ，Φ为常数。

本设计选取无人船相关参数[9]如表1所示。

表1 无人船相关参数

1.2 干扰模型设计

为了使仿真效果更符合实际情况，在仿真中加入风浪流的干扰。通过查阅文献可知，海流对无人船的干扰为一恒值，对船体模型影响较小可不考虑。而风浪对无人船的干扰可以通过白噪声和一个二阶波浪传递函数实现[10]：

(3)

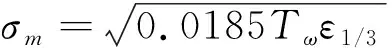
(4)

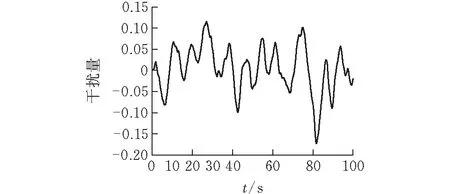
图 1 干扰信号

2 无人船航向控制算法

2.1 控制算法方案选择

传统PID控制算法多应用在线性Nomoto船体模型中，而将其应用到非线性Norrbin模型中发现超调量较大。模糊PID控制算法也大多用在线性Nomoto无人船模型中，相比传统PID控制算法具有更好的控制效果，但将其应用到非线性Norrbin无人船模型中时，超调量和稳定时间欠佳，抗干扰性能也较差。针对无人船航向控制系统模型存在模型参数和外界干扰不确定性的特点，也为了解决传统PID控制算法和模糊PID控制算法应用在非线性无人船模型抗干扰能力差、超调量和稳定时间欠佳的问题，本文提出了一种基于Backstepping的非线性无人船自适应航向控制算法。

2.2 控制算法设计

定理 对于一个由微分方程(2)表征的系统，通过构造一个正定的Lyapunov函数(7)，使该函数对时间的全导数负定(式(7))或半负定(式(10))，证明该系统的渐近稳定性。

证明 该航向控制算法稳定性证明过程由两步组成。

第一步 设定偏差变量

e1=x1-xd

(5)

e2=x2-Λ

(6)

其中：Λ为虚拟镇定函数，ξ为引入的积分项。构造无人船模型(5)(6)的第一个Lyapunov函数[12]

(7)

则V1对时间的导数

(8)

取虚拟镇定函数

(9)

其中，c1为大于0的待设定系数。将式(9)带入式(8) 可得

(10)

第二步 设定无人船模型全系统的Lyapunov函数

(11)

综上可得，无人船模型全系统Lyapunov函数对时间的导数

(12)

设定

F(x)=[x2x23]

(13)

(14)

将式(13)、(14)带入式(12)可得

(15)

设定θ的自适应控制率

(16)

设定舵角的控制律

(17)

(18)

将式(17)代入式(14)得

(19)

查阅资料可得

|γ|-1γ=sgn(γ)=sgn(b)

(20)

设定γ的控制律

(21)

将式(16)、(17)和(21)代入式(15)，并利用不等式x2+y2≥2xy可得

(22)

(23)

(24)

(25)

(26)

由上式可得

(27)

可知V2是呈指数形式衰减的，同时

(28)

因此，闭环系统的解是一致且最终有界的，且c1,c2,k1,k2,ρ,r1,r2,ε均为大于0的待设计参数。

3 仿真分析

通过查阅无人船船体参数[9]，计算可得Norrbin船舶非线性模型参数，其中K=8.2369，T=14.66，α=30°。

取定设计参数为c1=0.8,c2=5,k1=10,k2=10,ρ=10,r1=2,r2=2,ε=0.45,θ10=-0.012,θ20=-0.045。为了避免仿真结果的偶然性，实验设定了三组预期航向角，分别为30°，45°，60°，分别在Matlab里进行非线性Backstepping自适应航向控制算法、PID控制算法、模糊PID控制算法的航向控制仿真，结果如图2-7所示。

图 2 30°时航向控制算法对应的航向角变化

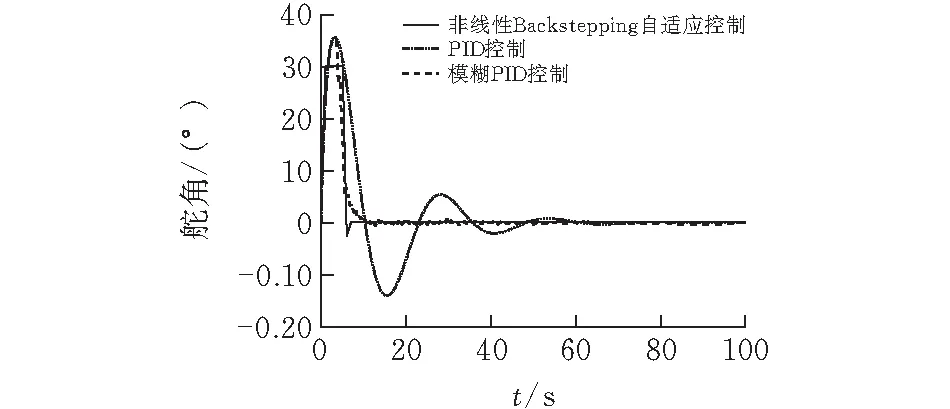
图 3 30°时航向控制算法对应的舵角变化

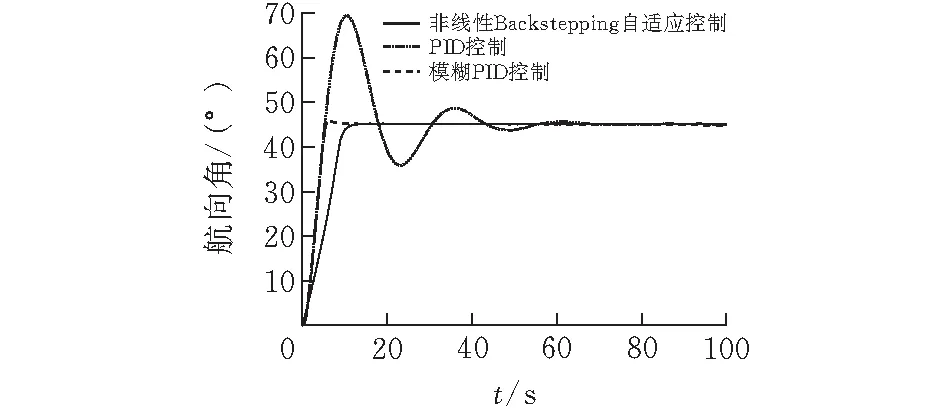
图 4 45°时航向控制算法对应的航向角变化

图 5 45°时航向控制算法对应的舵角变化

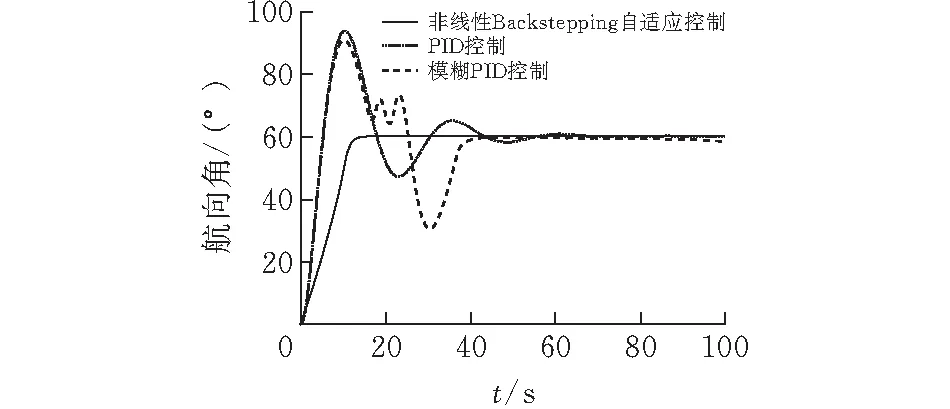
图 6 60°时航向控制算法对应的航向角变化

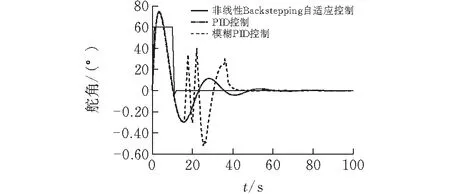
图 7 60°时航向控制算法对应的舵角变化

从图2-图7的仿真结果可得表2。

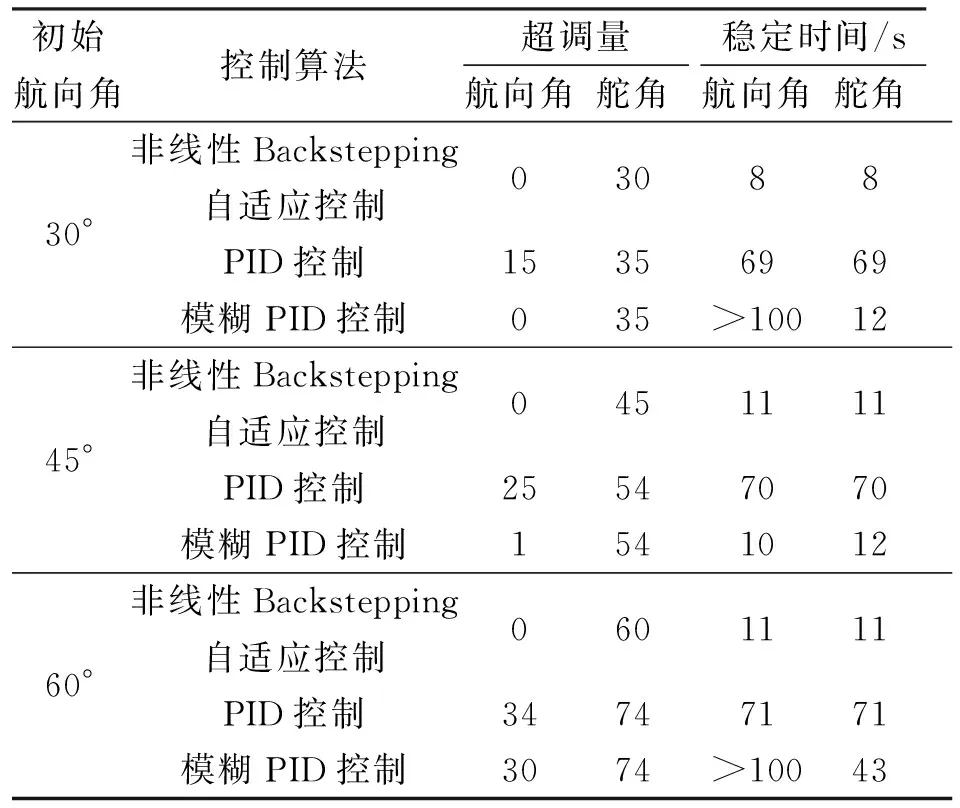
表2 仿真数据

由表2仿真结果可知：

1)在初始航向角为30°时，PID航向控制算法较其他两种算法超调量高15%;非线性Backstepping自适应航向控制算法的航向角稳定时间较其他两种算法至少减少61 s，且该航向控制算法较其他两种算法在舵角超调量上减少5；同时该航向控制算法在航向角稳定时间上仅为8 s。

2)在初始航向角为45°时，PID航向控制算法较其他两种算法超调量高25%;非线性Backstepping自适应航向控制算法在航向角稳定时间上较优，仅为11 s，且该航向控制算法较其他两种算法在舵角超调量上减少9；同时该航向控制算法在航向角稳定时间上仅为11 s。

3)在初始航向角为60°时，PID航向控制算法较非线性Backstepping自适应航向控制算法超调量高34%;非线性Backstepping自适应航向控制算法的航向角稳定时间较其他两种算法至少减少60 s，且该航向控制算法较其他两种算法在舵角超调量上减少14；同时该航向控制算法在航向角稳定时间上仅为11 s。

由上述数据分析可知，该非线性Backstepping自适应航向控制算法较其他两种航向控制算法具有较好的保持性能和动态品质。该航向控制算法不因初始航向角的不同而有过大的超调量。同时在参数变动及外来干扰的影响下，该控制系统具有较小的超调量和较短的稳定时间，说明该系统具有良好的抗干扰性能[13]。

4 结论

本文针对无人船航向控制Norrbin非线性系统，设计了一种基于非线性无人船的Backstepping自适应控制算法，借助Lyapunov函数验证了该算法可以使系统为最终一致且有界，并将该航向控制算法与PID航向控制算法和模糊PID航向控制算法进行对比，得出该控制算法在无人船非线性模型航向控制方面相比PID控制算法和模糊PID控制算法具有更好的抗干扰性能。