时间代价启发式多月基装备协同任务规划方法

赵宇庭，徐 瑞，于登云，朱圣英，李朝玉，赵志军，潘 博

(1. 北京理工大学宇航学院，北京 100081；2. 深空自主导航与控制工信部重点实验室，北京 100081；3. 中国航天科技集团有限公司，北京 100048；4. 北京空间飞行器总体设计部，北京 100094)

0 引 言

月球作为地球唯一的天然卫星，从古至今承载着人类的好奇与向往。随着各国月球探测计划的公布，新一轮的探月热潮正在兴起。中国和俄罗斯在2021年6月发布了国际月球科研站合作伙伴指南[1]，以月球构造、空间观测、原位资源利用等为科学目标，向国际伙伴发出邀请，就和平探索和利用外空月球开展合作。国内的学者从月球基地的研究任务、发展阶段[2]、结构形式[3-4]、月面机器人[5-6]等方面进行了研究和设想。美国国家航空航天局(NASA)的“阿尔特弥斯”计划，准备再次将宇航员送上月球[7]。由喷气推进实验室(JPL)主导的RLSO2(Robotic lunar surface operations 2)项目以建立一个可持续月球基地为目标，集结了任务设计、空间结构、月面机器人操控、自动化技术、原位资源利用、操作分析、载人任务和月面实验方面的专家，并研究利用水冰生产推进剂的技术[8]。德国宇航局研究了可通过机器人布置到月面的地球物理和天文学观测系统，并在月面模拟试验场验证了这种月球探测方式的可行性[9]。

从上述各国的探月计划可以看出，月球科研站的建设离不开月基装备。多种装备联合操作能够实现月球科研站中设施建设、天文观测、物料运输、原位资源利用等任务。用于特定任务的专门装备只需在其任务场地活动，而通用型装备需要在不同的任务场地间移动。物料运输装备不仅能服务多种任务，还需要在场地间多次往返传递物料。月球科研站空间范围大，地形复杂，装备在不同任务场地间移动会带来不可忽视的时间代价。如何在多装备间合理分配任务，降低路径转移代价，提高多任务执行效率，对月球科研站的建设有重要意义。而这一目标的实现有赖于任务规划技术的发展。

月球科研站构建任务规划中需要考虑多装备任务分配、装备调度、路径优化，又涉及单装备的动作规划、机械臂轨迹规划等因素，是一个综合性的复杂规划问题。此类任务规划问题往往以时间跨度或活动粒度分为多层进行规划，每一层有其相应的规划方法。如中国空间站的任务规划分为大粒度的月事件任务规划和小粒度的飞控操作规划[10]。德国宇航中心的ARCHES项目[11-12]，提出了一种高层任务控制流程，用任务路径图表示机器人的转移路径和多任务规划顺序，设计两步启发式算法求解多探测器合作的规划方案[13]，研究多异构机器人协同在月球低频无线电望远镜阵列布置、巡视和采样任务中的应用。然而此项目中机器人类型有限，没有考虑在同一路径上往返的物资运输活动。

欧洲的PRO-ACT计划[14]研究了异构多机器人在月面协同巡视、卸载物资、运输大型模块以及原位资源利用工厂装配任务的任务分配、任务规划以及机器人控制技术。采用了基于招投标的任务分配方法，基于时间线模型的合作多智能体任务规划、执行和监视方法，以及多机器人协同的轨迹规划和控制方法。在任务分配中，任务是由地面选择并逐个处理的，忽略了多个任务间的依赖关系和任务执行顺序的优化。

本文以月球科研站构建的上层任务规划问题为研究对象。装备通过原位任务执行、路径转移和物料运输三类大粒度活动，协同完成场景中的资源获取、设施建设、物料运输等任务。此规划问题可以看作多机器人任务分配领域的ST-MR-TA问题[15]，即每个装备同一时刻只能执行单项任务(ST)，一项任务需要多个装备(MR)协同进行，同一装备在一段时间内完成多项任务(TA)，即考虑装备的调度。除此之外，月球科研站构建中各任务间还存在时间约束，使此规划问题更为复杂。

在国内的月球表面装备规划研究中，文献[16]突出了月球车路径行为和其他行为耦合的特点，研究了单个月球车的任务规划技术；文献[17]研究了月球车的路径规划问题。在包含多个子任务的复杂场景下，多月基装备协同任务的规划方法尚待研究。

其他领域的任务规划方法可以为此问题提供参考，但难以直接应用。状态空间规划方法[18-19]以状态为搜索节点，而月球科研站构建场景中的任务、装备、路径都是状态中的变量，多变量的不同取值排列组合产生的巨大状态空间会降低规划效率。规划空间规划以部分规划为搜索节点，采用缺陷修复[20]或启发式搜索[21]进行规划，规划效率更高。两种方法都可以通过启发式策略[22-24]加速搜索，但现有启发式策略多以减少规划步数和解的规模为目标，对月球科研站构建任务规划关注的任务整体用时、装备转移路径选择、多装备任务分配等需求缺乏相应的优化机制。

本文针对月球科研站构建的多装备协同任务规划问题，建立相应规划模型。基于缺陷修复式规划的思想，将未安排时间的任务和任务未被满足的装备需求视作待修复的缺陷，将每一轮规划分解为任务选择、装备选择和装备活动安排三个阶段，并在缺陷修复的过程中加入优化机制。考虑场景中在固定区域发生的原位任务以及用于物资运输的路径任务的耦合关系，提出双类型任务关系图作为规划的基础。将月基装备在不同任务场地间转移的时间代价抽象成任务场景时间地图，基于此图求解多位置转移时间代价启发式策略以引导双类型任务关系图的搜索，优化任务规划顺序，从而缩短装备路径转移时间。设计时间代价启发式装备选择策略，为每个任务选择能尽早完成任务的装备组合。在装备活动时间线生成过程中构建任务活动混合时间约束网络，推理此网络生成具有时间灵活性的规划方案，并为时间代价启发式策略提供时间信息。

1 规划问题建模

本文的研究对象是包含多装备任务分配和活动安排的月球科研站构建上层任务规划问题，任务时间跨度持续数月，关注资源开采、物料转移、房屋建设等大粒度活动。

定义 1.月球科研站构建的多装备协同任务规划问题P可采用如下元组表示：

P=

(1)

式中：M为任务场景时间地图；T为需要完成的任务集合；R为任务可以采用的各类装备集合；S为任务活动混合时间约束网络；D为任务的最大允许时长。规划目标为利用集合R中的月基装备在时间D内协同完成T中的所有任务，规划的解包含各装备的活动时间线以及时间约束网络S。

定义2.任务场景的时间地图是一个以任务位置为点，任务位置间路径为边的加权有向图，边的权值是路径用时区间，表示如下式：

M=Vt,Et

(2)

式中：Vt={v0,v1,…,vi,…,vn}为位置点集合，每个位置点由二维坐标表示vi=xi,yi，场景中的初始点v0是任务开始前存放所有装备的大本营；Et={e0,e1,…,ei,…,en}为路径集合，每条路径表示为：

ei=vi,vj,[dmin,dmax]

(3)

式中：vi为起点，vj为终点；[dmin,dmax]为路径权值；dmin为装备通过路径的最短用时，dmax为最长用时。图1展示了包含三个位置点的场景时间地图，其中从点i到点k的路径用时最短为10，最长为20，从k到i点的路径用时最短为20，最长为35。两点间往返用时不同是为了更好地描述月球表面地形高低起伏和障碍物对装备行走时间的影响。利用此图中的时间信息，可以估计任务路径耗时和装备完成任务所需的时间。

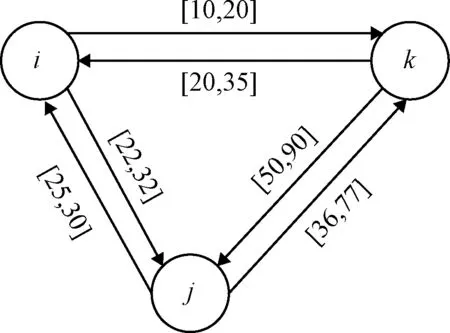
图1 包含三个位置点的任务场景时间地图Fig.1 Time map of a mission scenario with three locations

根据月球科研站构建任务的特点，将所有任务分为原位任务和路径任务。原位任务的执行空间是位置点附近的有限范围，通常需要多月基装备合作完成，比如资源采集、设备组装、房屋建设等。路径任务的执行空间是场景中的路径，通过装备的移动在路径上运输原位任务所需的物料，例如月壤、水资源、建筑模块及设备组件等。结合两种类型任务的信息，形成统一的任务定义。

定义3.任务可以定义为一个元组，包括任务名称、任务位置、时间和资源约束、对装备的需求、任务类型、与其他任务间依赖关系和执行后产生任务效果。具体表示如下式：

t=N,L,Ct,Cr,R,l,Prel,Prep,Eff

(4)

式中各项的含义如下：

1)N为任务名称；

2)L为任务位置参数，原位任务的位置为位置点v，路径任务的位置为路径e，与任务场景时间地图中定义的点和路径一致；

3)Ct=[smin,smax],[emin,emax],[dmin,dmax]为时间约束，用任务开始时刻、结束时刻和持续时长的允许范围表示；

4)Cr=r,nr为资源约束，需要在任务执行前满足，其中r为资源名称，nr为资源量，路径任务的路径起点即为资源所在位置，每个路径任务只能运输一种资源，因此只有一个资源约束，而原位任务的资源需求通过其依赖的路径任务实现；

5)R={a1,n1,a2,n2, …,ai,ni, …,an,nn}为此任务对装备的需求，用二元组集合表示，二元组的第一项ai为装备能力，用装备能力而非装备类型描述任务对装备的需求是因为单个装备可以具备多种能力；第二项ni为装备数量需求，对于路径任务，此值为任务允许调用的装备数上限，对于原位任务，此值为任务需要的装备数量；

6)l∈{1,2}为任务类型，1代表原位任务，2代表路径任务；

7)Prel=c1,T1,c2,T2为此任务依赖的原位前提任务集合，二元组的第一项表示前提的约束类型的字符串，有开始型前提c=“st_st”和结束型前提c=“et_st”，第二项表示前提任务集合T={t0,t1, …,ti, …,tn}；

8)Prep=c1,T1,c2,T2为此任务依赖的路径前提任务集合，同样根据前提约束类型分为开始型和结束型两类；

9)Eff为资源效果和装备状态改变效果，资源效果指此任务在某位置点增加或减少的资源，装备状态改变指装备中添加完成此任务的活动及装备位置的变化，资源效果是提前定义的，装备状态改变在规划中根据决策产生。

任务集合T={t0,t1, …,ti, …,tn}包含所有当前问题中需要规划的任务。

定义 4.月基装备是具备一种或多种能力的在月面工作的装备，包括着陆器、巡视器和特种机器人等，表示如下：

r=Nr,A,c,Tl,p

(5)

式中：Nr为装备名称；A={a0,a1, …,ai, …,an}为装备能力集合；c为装备运输容量；Tl={act0,act1, …,acti, …,actn}为装备的活动时间线，一个按时间先后排列且互不重叠的活动序列。本规划方法生成的时间线具备时间灵活性，即活动的开始时刻、结束时刻及持续时长以可行区间形式表示。p为装备当前位置。

定义 5.任务活动混合时间约束网络是以任务或活动的开始、结束时刻为节点，以时间约束为边的有向图，表示如下：

S=Vs,Es

(6)

式中:Vs为点集，Es为边集，边集为Vs阶方阵。点集中设置时间零点，作为任务规划的时间参考点。从点i指向点j的边eij表示两点间的时间关系为tj-ti≤eij。在规划开始时，时间约束网络中只有时间零点，随着任务规划的进行，逐步加入新的点和边。网络中既有表示任务的点也有表示活动的点，任务间的约束通过任务与活动的绑定关系传播到活动之间。

2 时间代价启发式规划算法设计

提出基于双类型任务关系图搜索的启发式规划，设计时间代价启发式策略，以在满足复杂约束的同时优化任务用时。设计多位置转移时间代价启发式任务选择策略以引导双类型任务关系图的搜索方向，减小路径转移代价。选定任务后，依据时间代价启发式装备选择策略为任务分配合适的装备组合。完成每个任务的装备分配后，更新任务活动混合时间约束网络并进行约束推理，生成时间灵活的活动方案。当前部分规划中任务和活动的时间信息是后续规划中求解时间代价启发式策略的基础。

2.1 基于双类型任务关系图搜索的启发式规划

原位和路径任务的耦合是月球科研站建设任务的突出特点。因此，提出双类型任务关系图表示任务间的耦合关系。

定义 6.双类型任务关系图是以两种类型的任务(原位任务、路径任务)为节点，以任务间的约束为边的有向无环图。图中的边由前提任务指向当前任务，边值为表示前提约束类型的字符串(“st_st”或“et_st”)。

图2展示了双类型任务关系图的结构，圆形节点代表原位任务，方形节点代表路径任务，边代表优先约束。“st_st”型约束(图中虚线箭头)表示当前任务在前提任务开始后即可开始，前提任务在当前任务结束前结束。“et_st”型约束(图中实线箭头)表示当前任务要在前提任务结束后才能开始。

根据双类型任务关系图的结构，逐个规划原位任务及其依赖的路径任务，就能够得到一套可行的规划方案。但对于月球科研站建设任务，仅求可行解显然难以满足实际需求。因此，构建任务场景时间地图，利用此图的信息求解时间代价启发式任务选择策略和装备选择策略，使规划解不仅满足约束还具备时间优化效果。

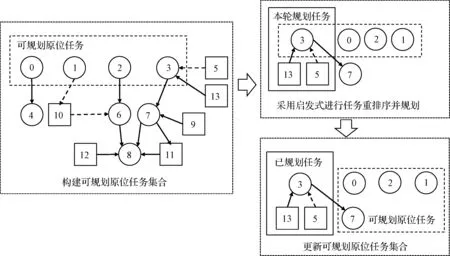
图2 基于双类型任务关系图搜索的规划流程Fig.2 Planning process based on the dual-type task relationship graph search

规划算法以双类型任务关系图中的原位任务为脉络，路径任务为分支，由多位置转移时间代价启发式策略决定搜索方向。规划流程需要借助三个任务集合实现：未规划原位任务集合U，已规划原位任务集合D，当前可规划原位任务集合O。规划流程见图3，其中具体步骤如下：

1)从问题文件中读取任务，加入任务集合U。

3)采用多位置转移时间代价启发式策略对O中的任务进行排序，排序后取O中第一个任务t。

4)采用多位置转移时间代价启发式策略对任务t的路径前提任务集合Prep中的任务排序。

5)规划任务t的路径前提任务集合Prep中的任务。根据物资运输量、各装备运输能力、物资运输路径、装备当前位置和时间线上的历史活动，采用时间代价启发式装备选择策略选择能最早运输完物资的k辆装备(k不大于允许此任务调用的装备数n)，并确定运输物资需要的总运输次数nt。

6)向装备添加完成此路径任务的活动。若装备位置不在路径起点，在装备时间线上添加移动活动，使装备移动到路径起点。若装备在路径起点，直接添加运输活动。将运输活动的相关约束加入时间约束网络，依据网络推理结果提取活动时间参数。时间约束网络中包含任务和活动的绑定约束，能够保证活动时间更新后任务时间也随之更新。

图3 双类型任务关系图启发式规划流程图Fig.3 Flow chart of dual-type task relationship graph heuristic planning

7)采用时间代价启发式装备选择策略为原位任务t选择装备组合，并在装备的时间线上添加以任务位置为终点的路径转移活动。

8)将原位任务t加入装备活动时间线。首先将任务加入时间约束网络中，然后将原位任务的活动加入到上一步选择的装备中。添加活动的同时，将活动和任务相关的时间约束加入时间约束网络，并进行推理。根据时间约束网络推理的结果给活动和任务的时间参数赋值。

9)更新任务集合，将t从未规划原位任务集合U及当前可规划原位任务集合O中剔除，加入已规划原位任务集合D(规划开始时为空集)。

重复步骤(2)到(9)直到满足任务规划结束条件：集合U及集合O都为空。

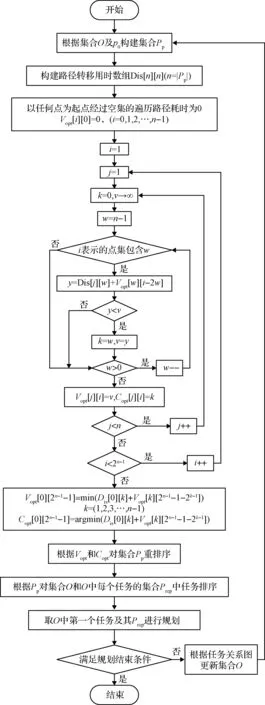
图4 多位置转移时间代价启发式求解方法Fig.4 Time-cost heuristic calculation method based on the multi-location transfer time

2.2 多位置转移时间代价启发式任务选择策略

月球科研站构建任务中包含多个子任务，不同的任务可能会需要具有相同能力的装备，由此引发装备在不同任务位置间的移动。因此路径转移的时间将对整体的任务用时产生很大的影响，规划中可以通过优化任务的规划顺序减少装备路径转移用时。

常见的启发式策略先对每个候选节点进行评价，再从中选择最优节点。多位置转移时间代价启发式策略采用了一种新的候选节点评价思路，不评价每个节点的代价，而是评价遍历多个节点的不同排序方案的代价，然后选取代价最低的方案中第一个未规划节点作为决策结果。

定义 7.多位置转移时间代价启发式策略是一种基于时间代价的双类型任务图搜索方向引导策略。该策略求解遍历多个任务点的最短路径，并取此路径中的第二个点作为下一个被搜索的节点(路径起点为上一个已规划任务所在位置，其它点为集合O中所有任务的位置)。

如图4所示，在每一轮规划中，提取集合O中每个任务的位置p组成位置点集合Ph，任务集合D中最后一个任务的位置p0。当D=∅，p0=v0，v0为场景中的初始位置。求解以p0为起点，遍历Ph中所有点的最短耗时路径Pp。路径转移用时从场景时间地图M中提取，取路径的最短允许时长用于时长估计。

多点遍历最短路径问题与旅行商问题[25]相似，具有最优子结构性质，适合采用动态规划方法求最优解。用矩阵Vopt[j][i]存储以j(j∈Ph)为起点，经过i表示的点集(集合Ph/p0的子集)的最短路径的长度，矩阵中各元素初始值为无穷。用Copt[j][i]存储最短路径的第二个点，元素初始值为空。其中，i为用状态压缩法表示的节点集合，将i转换为二进制数后，第n位为1表示集合包含节点n，第n位为0表示集合不包含节点n。

遍历i,j的值域并更新Vopt[j][i]和Copt[j][i]能够避免同一点集最短遍历路径的重复计算，提高求解效率。

得到两个矩阵后，再从中提取最短路径方案Pp。集合O中的任务按任务位置在Pp中的顺序排序，集合Prep中的任务按路径起点在Pp中的顺序排序。集合O中第一个任务即此轮规划即将处理的任务。此轮规划结束后，更新集合O并在下一轮规划中再次调用启发式策略选取最佳任务进行规划，重复此过程，直到规划结束。

用图5说明上述启发式策略实现的增量式任务路径更新效果。图中的点代表任务，有向边的长度表示从出点到入点的位置转移时间代价。采用多位置转移时间代价启发式策略对任务排序后，得到装备从上一个已规划任务位置(虚线圆点)出发遍历集合O中所有任务位置的最短用时路径，下一个待规划的任务从任务0变为任务1。完成任务1的规划后，规划算法更新集合O，剔除已规划的任务1，加入以任务1为唯一前提的任务4，再次采用启发式策略对任务排序。

图5 基于路径用时的增量式任务排序Fig.5 Incremental task sorting based on path time

2.3 时间代价启发式装备选择策略

任务选择策略选定的任务需要适合的装备来完成。以可行解为目标的任务规划方法，只要求装备的功能符合任务需求，不考虑不同的装备组合对任务完成时间的影响，容易因装备选择不当而浪费装备资源、延长任务耗时。

考虑运输装备的历史任务对新任务开始时刻的影响，装备数量与路径任务用时并非严格负相关。因此，路径任务需要在装备分配数量上限n以内选择最早完成任务的装备组合。原位任务对各类装备的需求量和任务用时是给定的问题输入参数，影响任务完成时间的主要因素是装备到达任务位置的时刻。

为了方便遍历，路径任务的启发式装备选择策略将所有装备组合信息压缩为从1到2k-1(k=R，R为装备集合)的整数。在路径代价求解时，将整数i转换为k位二进制数字，数字的第n位为1表示此组合里包含装备n。从所有装备数不超过装备分配数量上限n的组合中选择时间代价最小的作为此路径任务的装备集合。

时间代价指装备组合Rc完成此路径上的物资运输任务的最早预计结束时刻。算法根据任务场景时间地图估计装备在路径p上反向移动一次需要的时间dre：

dre←M.getpath(p.get_vj(),p.get_vi()).get_dmin()

(7)

将此路径任务的“et_st”型原位前提任务的最早结束时刻、“st_st”型原位前提任务的最早开始时刻，以及各装备到达路径起点的最早时刻加入集合Ttmp。对Ttmp中的元素取最大值用于预测路径任务的最早可能开始时刻。

装备从路径p的起点出发，经过几次往返后在路径终点结束物资运输，按此运输模式估计路径任务的时间代价cR：

cR←max(Ttmp)+「nt/Rc⎤·(p.get_dmin()+

dre)-dre

(8)

其中，nt为多个装备合作需要的总运输次数，由物资量nr除以单装备运输能力l后向上取整得到：

nt←「nr/l⎤

(9)

确定装备组合后，将路径转移活动和运输活动加入各装备的时间线中。每辆运输装备的运输活动数采用如下方法计算：将总运输次数除以车数后取整，得到每辆车的基础运输次数nb：

nb←[nt/k]

(10)

余下的运输次数则逐个分配给较早到达运输起点的若干运输装备。

原位任务的装备选择策略则较为简洁，收集所有符合能力条件的装备，比较其完成历史任务后沿路径到达当前任务场地的最早时刻ta：

(11)

2.4 任务活动混合时间约束网络推理

为了应对月球科研站构建任务中的不确定因素，需要通过时间约束网络的构建和推理实现规划的灵活性。添加新的任务、活动、约束或改变活动时间后，要在时间约束网络中进行约束推理。再从推理的结果中提取出任务或活动的开始时刻、结束时刻、持续时长的可行区间。在下一轮规划中，这些信息作为时间代价估计的输入，影响后续的活动安排方案。

图6 任务活动混合时间约束网络Fig.6 Hybrid time-constrained network for task activities

规划中的任务和活动在时间上是相互耦合的，活动要符合任务的时间约束，任务的完成时间受活动的影响。如图6所示，任务活动混合时间约束网络中既有表示任务的点也有表示活动的点，一个任务或活动由开始、结束两个节点表示。点1, 2表示任务0，点3, 4表示任务1，点5, 6表示任务2。图中的边表示约束，约束不仅存在于任务之间、活动之间，也存在于任务和活动之间。

图6中的0, 1, 2三点间的六条边表示了任务自身的时间约束，点1表示开始时刻，点2表示结束时刻。边的权值如图7所示，vs为开始时刻，ve为结束时刻，边上的权值表示开始结束时刻的允许范围，以及持续时长的允许范围。

图7 向时间约束网络加入新任务或活动Fig.7 Adding a new task or new activity to the network

任务间的前提约束通过属于不同任务的点之间的边表示。图6中点3与点2之间的边表示任务1与任务0之间为“et_st”型约束，即任务1在任务0结束后开始。点2与点5之间的边和点4点6之间的边，表示任务1与任务2之间为“st_st”型约束，即任务2在任务1开始后开始，在任务1结束前结束。任务间的时间约束也需要传递给活动，由于任务0是任务1的前提，完成任务1的活动的节点9与任务0的结束节点2之间也存在前提约束。此外，属于同一个装备时间线的活动间天然存在前提约束，如节点9与节点8之间的边表示绿色活动在蓝色活动之后。

图8 向时间约束网络加入有前序约束的活动(任务)Fig.8 Adding a new activity (task) with priority constraint to the temporal network

前序约束的具体表示如图8，其中vpre为前提节点，D为任务场景的时长，表示此活动(任务)的开始时刻vs在前提节点表示的时刻之后。

任务与完成它的活动间存在包含约束。图6中由点7、点8表示的装备0的活动及由点11、点12表示的装备1的活动能够完成节点1, 2表示的任>务，任务与活动间的边表示包含约束。图9展示了一个任务和一个活动间包含约束对应的边值，代表任务在活动开始前开始，在活动结束后结束。

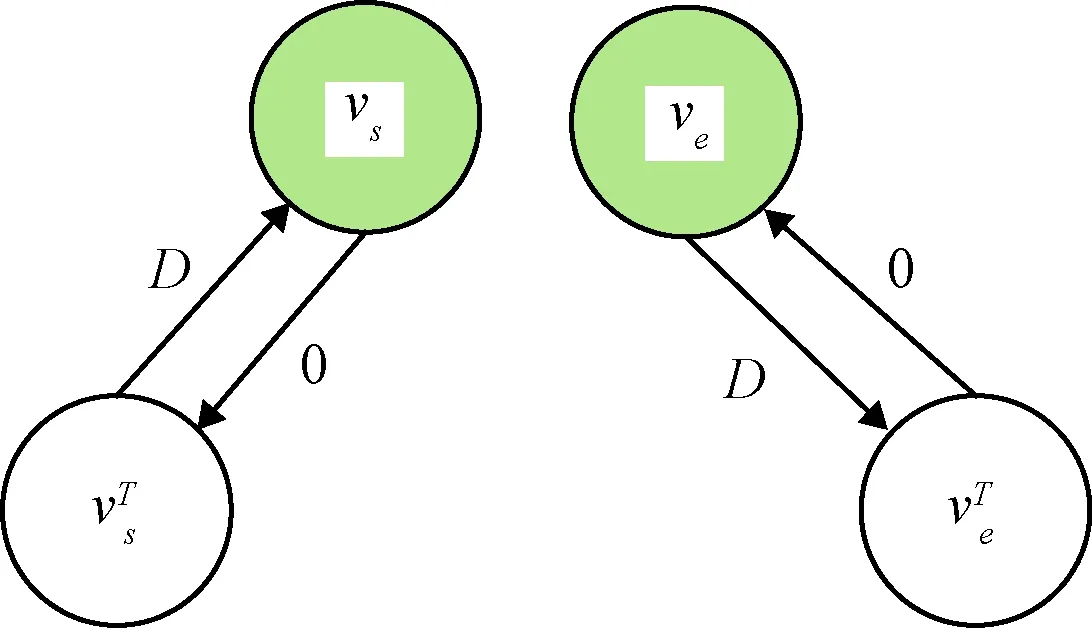
图9 向时间约束网络添加包含约束Fig.9 Adding a inclusion constraint to the network

协同完成同一个原位任务的多个装备的活动间有并行约束，即不同装备完成同一个任务的活动的开始、结束时刻相同。要表示两个节点时间同步，只需将两点间的两条边的权值都设为0。

月球科研站构建任务规划中时间约束复杂，时间约束图中的边多于点，是一个稠密图。因此采用适合稠密图多源最短路径求解的Floyd-Warshall算法[26]。时间约束推理后，再提取网络中的边值，为活动和任务的时间参数赋值。

3 仿真校验

3.1 场景设计

为了说明规划方法的效果，设计任务场景进行仿真。场景包含资源获取、电站建设、房屋建设等任务，场景时长为15000 h。图10为所有任务及任务间约束。

如图11所示，场景中有7个随机选取的位置点，0点代表所有装备的初始着陆区域的中心坐标，其余点代表原位任务区域的中心坐标。

图10 月球科研站构建场景的双类型任务关系图Fig.10 Dual-type task relationship graph of the lunar scientific research station construction scenario

图11 任务场景地图Fig.11 Mission scenario map

土壤运输任务的起点为1，终点为3；水资源运输任务的起点为2，终点为3；电站模块运输任务的起点为0，终点为4；建筑材料运输任务的起点为3，终点为5；建筑模块运输任务的起点为5，终点为6。为了模拟月面的高低起伏，0点设为场景中的最低点，远离0点的路径耗时多，趋近0点的路径耗时少。

表1展示了每个任务的用时区间及装备需求，用<能力，数量>表示原位任务的装备需求，<能力，数量，运输资源量>表示路径任务的装备需求。图10中的边表示任务间约束关系。月壤采集任务的资源效果是月壤3000单位，水资源采集任务的资源效果是水资源2000单位，建筑材料生成的效果是4000单位材料，建筑模块制造的效果是400个模块。

表1 任务需求信息Table 1 Mission requirements

表2展示了场景中的装备，装备的能力代表其可以进行的活动。按照未来的技术发展趋势，设置了若干多功能装备。除了表中列出的功能外，每个装备都具备移动能力。

表2 装备功能信息Table 2 Robot functions

3.2 对比分析

为了验证规划方法的有效性，用Java实现规划算法并对所设计的任务进行规划。仿真测试环境为：Windows10 64位操作系统，i5-1035G1 CPU，主频1.00 GHz，内存16.0 GB。

将规划问题以JSON格式文件的形式输入到规划器中，规划后输出装备活动时间线，并统计任务总时长、装备工作时长等参数。为了验证规划方法的有效性，用三种算法规划同一问题。三种算法分别为：缺陷修复式规划、基于招投标机制的规划、双类型任务图时间代价启发式规划。缺陷修复式规划将未规划的任务和任务未满足的装备需求视作缺陷，按任务集合的生成顺序处理原位任务和路径任务，按装备加入集合的初始顺序依次采用装备。基于招投标机制的规划按任务加入集合的顺序逐个进行任务招标，符合条件的装备组成团队进行投标，最早完成任务的装备团队中标，与时间代价启发式装备选择策略等效。本文提出的双类型任务图时间代价启发式规划方法，用多位置转移时间代价启发式任务选择策略决定任务规划顺序，并采用时间代价启发式装备选择策略为每个任务选择装备集合。

分别采用无任务选择策略、单次转移时间代价启发式任务选择策略和多位置转移时间代价启发式任务选择策略进行规划，并对比其形成的任务路径。任务路径的最短用时见表3,相应的任务路径如图12所示。

表3 原位任务路径Table 3 In-situ task paths

单次转移时间代价启发式任务选择策略仅根据新任务与上一个已规划任务间的路径用时选择任务，不预测后续任务对路径的影响，因此其生成的任务路径用时要长于多位置转移时间代价启发式任务选择策略。

图12 不同任务选择策略下的原位任务路径对比Fig.12 Task paths generated by different strategies

统计每个装备的时间线上最后一个活动的最早允许结束时刻，表示此装备完成任务所需的工作时长。

图13展示了三种方法得到的各装备工作时长，启发式任务选择策略和装备选择策略有效降低了任务耗时。只求可行解的缺陷修复式规划方法得出的方案至少耗时13689 h完成场景中所有任务，基于招投标机制的规划方法得出的方案需要8963 h，本文提出的规划方法得到的方案仅需要8161 h。从图中折线的走势可以发现，任务中用时较长的装备是具备运输能力、碎石能力和装配能力的装备，这些装备需要在多个任务中共用，优化它们的任务时长是减少任务总耗时的关键。

图13 不同规划方法下的装备工作时长Fig.13 Working time of the robots with different methods

如表4所示，本文提出的方法得到的规划方案比缺陷修复式规划方法节约28.95%的多装备总用时，说明多位置遍历时间代价启发式任务选择策略和时间代价启发式装备选择策略不仅能减少任务用时，还可以缩短装备的活动时长。

表4 多装备总工作时长Table 4 The total working time of the robots

图14展示了三种方法得到的规划方案的各装备的任务路径，用不同的颜色和线宽区分装备，路径相同的多个装备用同一条较粗的曲线表示，各装备在同一段路径上的往返运输次数由文字标注。

对比前两个路径图中从点0到点4的电站模块运输任务，缺陷修复式规划方法得到的方案需要装备1,2,3往返5次，装备0往返4次，基于招投标机制的规划方法得到的方案需要装备2,3往返6次，装备0往返7次，说明装备选择策略优化了任务的装备选择方案。虽然任务需求中允许给此任务分配四个装备，但采用三个装备能更高效地完成任务。同样的，从点3到点5的建筑材料运输任务经过装备选择策略的优化，选择了2,3,4三个装备实现40次运输，而不是选择4个装备各往返10次。

图14 三种方法的多装备任务路径对比Fig.14 Task paths of the robots with different methods

本文提出的方法得到的方案中装备9,10,11在位置4和位置6之间没有来回折返。因为多位置转移时间代价启发式策略优化了任务规划的顺序，装备可以连续完成位于相同位置的任务，然后再前往下一个位置，从而避免装备在不必要的路径转移活动上浪费时间。

每种规划方法对任务进行十次规划，并取计算时间的平均值，结果如图15所示。相比其他两种方法，双类型任务图时间代价启发式规划方法的规划效率更高。此结果说明启发式策略不仅能优化任务收益，还能提高规划效率。虽然采用启发式策略进行任务和装备评估需要时间，但也能使装备任务路径更简洁，减少约束网络中的节点数量，缩短约束网络推理的时间，从而提高了整体的计算效率。

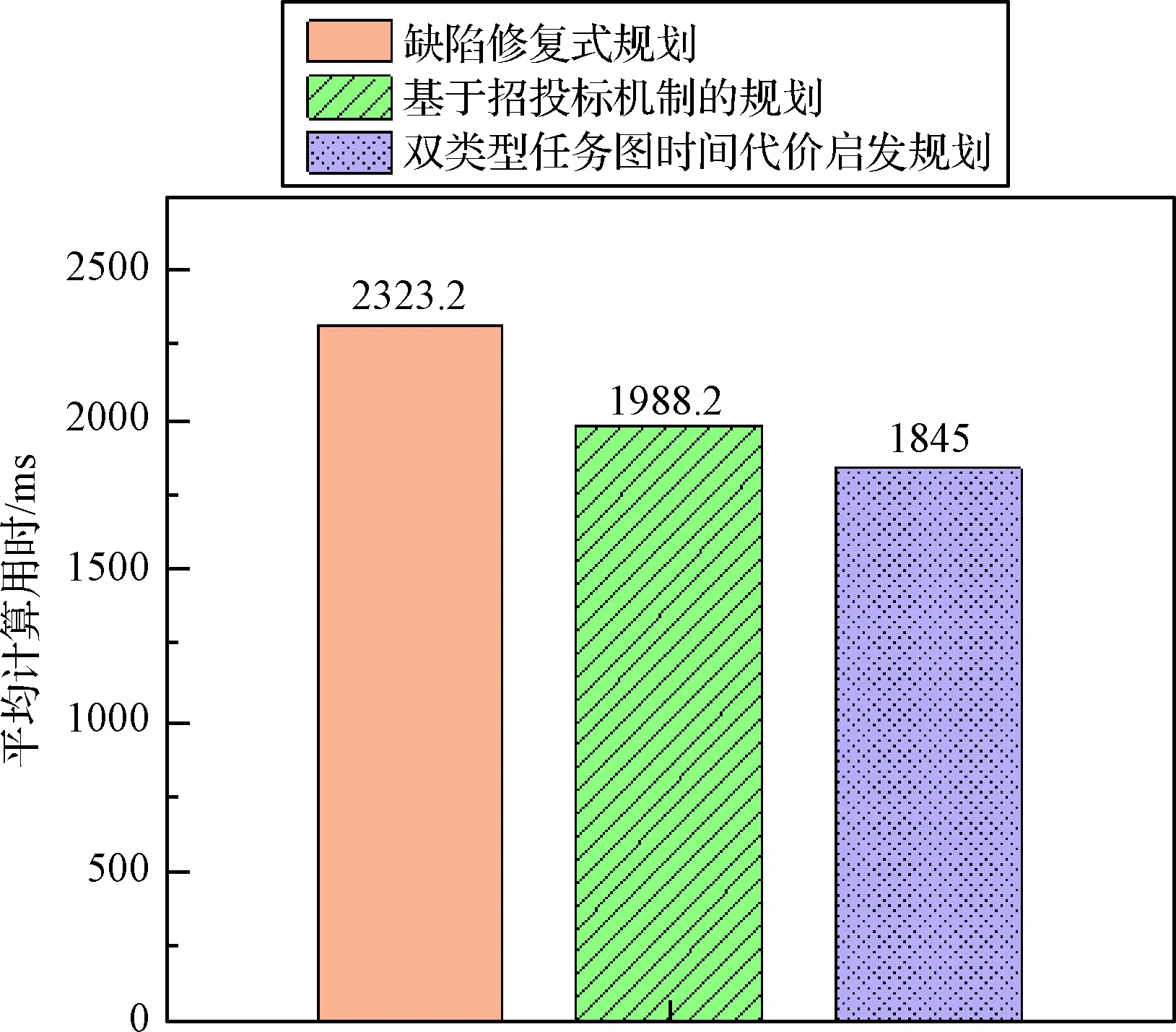
图15 平均计算用时对比Fig.15 Average calculation time comparison

为了应对任务中的不确定因素，本文提出的方法构建了时间约束网络，在网络中进行约束传播，得到时间灵活的规划方案。

表5展示了装备0,1的活动时间线，每个装备有三种类型的活动，移动活动表示为<移动，起点，终点，开始时刻区间，结束时刻区间>，物资运输活动表示为<任务名，起点，终点，往返次数，开始时刻区间，结束时刻区间>，原位活动表示为<任务名，开始时刻区间，结束时刻区间>。活动的开始、结束可以根据实际情况选取具体执行时刻。

表5 时间代价启发式规划方法得到的规划方案Table 5 Plans generated by the proposed method

取每个活动的最早开始时刻和最早结束时刻绘制甘特图(见图16)。图中各装备的活动安排满足任务间的前提约束和协同装备间的并行约束，符合各任务对装备类型和数量的要求。任务时间安排紧凑，所有任务都能在前提条件满足后及时开始。例如，装备4结束电站模块运输后，装备0,1,9,10,11立即开始建设电站。建筑模块运输时，场地平整任务也同步展开，场地平整完成后，紧接着开始建筑建设。受益于规划算法对任务路径的优化，装备在完成土地平整任务后，可直接在原地完成后续的设施建设任务，避免了路径转移耗时。在时间代价启发式装备选择策略的作用下，相同功能的多个装备的任务负载较为均衡。以运输任务为例，没有出现某些装备完成大部分任务，而其他装备空闲的现象，从而节省了任务总体用时。

4 结 论

本文针对月球科研站构建的任务规划问题，提出时间代价启发式多月基装备协同任务规划方法。考虑月基装备路径任务与原位任务耦合的特点，设计双类型任务关系图作为规划基础。针对月球科研站构建任务的时间优化需求，提出了多位置转移时间代价启发式任务选择策略，通过优化任务规划路径缩短装备路径转移用时；提出了时间代价启发式装备选择策略，能够均衡多装备任务负载、缩短整体任务用时。构建任务活动混合时间约束网络并采用多源最短路径算法进行推理，使规划方案具备时间灵活性并为启发式策略提供时间信息。本文提出的方法能够生成满足复杂时间约束的规划方案，具有可行性；用可行范围表示活动时段，具有时间灵活性；与缺陷修复式规划和基于招投标的规划方法相比，装备的任务分配更合理、任务用时更短，具有时间优化性。本文提出的方法能够为未来的月球科研站构建任务提供规划技术支持。

图16 各装备活动时间线的甘特图Fig.16 Gantt charts of the robots activity