刚柔混合双臂空间机器人抓持-操作协同规划

胡忠华，徐文福，杨太玮，梁 斌

(1. 聊城大学, 聊城 252000; 2. 哈尔滨工业大学(深圳)，深圳 518055; 3. 清华大学，北京 100084)

0 引 言

近年来，在轨服务引起了各航天大国的关注，并且正在成为空间技术发展的重要领域之一[1-3]。在轨服务主要是为太空中的航天器提供在轨操作，如燃料加注、故障部件维修和关键模块安装等。然而，上述任务的操作对象往往处于部分封闭的环境中，如狭窄平面空间或狭窄弯曲空间，将为空间机器人完成对目标卫星在轨操作带来巨大的挑战。

由于双臂机器人系统在协同操作中具有较高的精准度、高效率和灵巧性等优点，被广泛应用于各种生产场景中，如部件组装、物品分拣及商品包装等[4-5]。同样地，基于双臂机器人的上述优点，它们也被用于在轨服务操作任务中[6-7]。与地面双臂机器人不同，在轨双臂机器人的基座处于自由漂浮状态，当双臂协同执行在轨操作时会对基座造成扰动，而基座的运动又会带动机械臂运动从而影响双臂末端的操作精度[8-10]。另外，当在轨操作环境受限时，还需要考虑双臂协同运动中避免与周边的物体发生碰撞，因此它对在轨服务双臂机器人的灵巧性以及协同规划算法有更高的要求。目前，双臂协同运动主要包括主从协同规划、多优先级协同规划以及基于避障策略的协同规划[11]。Chen等[12]提出了一种始终保持基座固定的空间双臂捕获目标的轨迹规划方法。其中一个机械臂为任务臂，采用多项式插值方法实现末端点到点规划，另一个机械臂为平衡臂，用以实现基座的稳定。但该方法仅能适用于二维平面双臂空间机械臂，且待捕获的目标处于静止状态。为了实现对运动目标的捕获，Wu等[13]利用一种无模型强化学习策略实现了双臂协同捕获运动目标的在线轨迹规划。但文献[12]和[13]在进行双臂协同规划时并未考虑操作环境中出现障碍物的情况。为了解决上述问题以实现受限空间中的协同规划，Nithya等[14]设计了一种静态避障的准则，可以在任意时刻避免与障碍物发生碰撞。但该避障方法仅可实现离散约束空间的避障，而不能用于连续约束空间(狭窄平面约束、弯曲管道约束)中的避障规划。

此外，在太空任务操作中，机械臂的可操作度指标也是空间机器人领域的研究热点之一。Yoshikawa[15]最早提出了可操作度的概念，用以确定各种类型的关节机器人的最优姿态，但这些机器人的基座均为固定形式。文献[16]分析了漂浮基平面两自由度空间机器人的可操作度，同时得到了该平面空间机器人的工作空间，但此文献中的相关理论很难直接应用于三维多自由度的空间机器人。Nenchev等[17]推导了FAR(Fixed-attitude-restri-cted)雅可比矩阵，提出了FAR可操作度的概念并以基座扰动大小的程度衡量空间冗余机械臂任务操作性能，但该方法仅对单臂空间机器人的可操作度进行了分析。对于多臂空间机器人，张博等[18]分析了辅助臂和基座对任务操作臂耦合作用下的可操作度，实现了空间双臂机器人的构型优化，但没有考虑双臂操作目标中系统形成闭链时对机械臂可操作度的影响。为了解决这一问题，Xu等[19-20]对闭链时多臂空间机器人的可操作度进行了分析，并将自由漂浮闭链系统的可操作度椭球、可操作度和任务兼容性等理论进行了拓展。闫磊等[21]提出了一种多目标优化的双臂协调规划方法，其中一个优化目标为机械臂的可操作度，可使得双臂的操作度最大，但没有考虑当操作环境受限时机械臂的可操作度优化问题。

综上所述，在以往的文献研究中，要么仅解决了双臂协同规划问题，要么仅解决了机械臂的可操作度优化问题，极少将这两个问题同时考虑并加以解决。因此为了同时解决以上两个难题，本文提出了一种基于受限空间可操作度优化的刚柔混合双臂协同轨迹规划方法。该方法不仅可实现刚柔混合双臂的协同规划以完成狭小平面空间的穿越，还可实现操作臂在任务操作方向上的可操作度优化，使其具有更大的任务操作能力。

1 刚柔混合双臂空间机器人建模

1.1 混合双臂空间机器人构型设计

传统的空间双臂系统一般装载两个相同的刚性机械臂，此刚性臂类似于工业机械臂，驱动电机和控制器集中于关节处，体型较大难以完成受限空间的操作任务。如图1所示，与传统的双臂空间机器人不同，本文设计的混合双臂空间机器人系统包含两个结构不同的机械臂，其中一个与上述刚性臂类似，为无偏置刚性机械臂，另外一个是分段联动绳驱柔性臂。这种设计方式的优势为：刚性臂整体刚度大、负载强有利于实现目标卫星的抓捕，而绳驱柔性臂的灵巧性和灵活性高，有利于实现目标卫星上受限空间内的任务操作。

其中，无偏置刚性臂有7个自由度，采用R-Y-R-Y-R-Y-R的关节配置。绳驱柔性臂则由5个相同的联动段组成，每个联动段共有n(n为偶数)个模块化联动关节，且每个关节均为万向节。对于第i个关节，若i为奇数，此关节的配置为P-Y型，当i为偶数时，关节配置为Y-P型。一个模块化关节和连接在此关节上的一个刚性臂杆组成了一个子节。因此可知，每一个联动段包含n个结构相同的子节。由于联动作用，每个联动段中相当于仅有1个自由运 动的关节(即第1个万向节)，其余关节与第1关节保持联动运动。因此，对于上述分段联动绳驱柔性臂，它的自由度数为10。

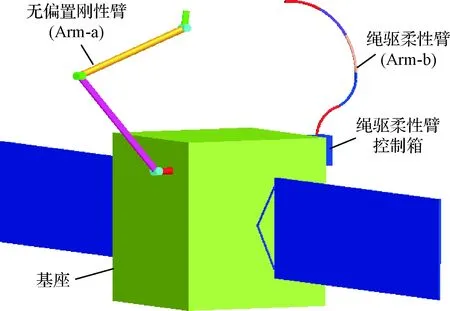
图1 混合双臂系统的构型设计Fig.1 Configuration design of the hybrid dual-arm system

1.2 混合双臂空间机器人运动学建模

刚柔混合双臂系统广义模型如图2所示。图中各个符号的含义可参考文献[22]和文献[23]。根据传递关系可知刚柔双臂末端的位置矢量分别为

(1)

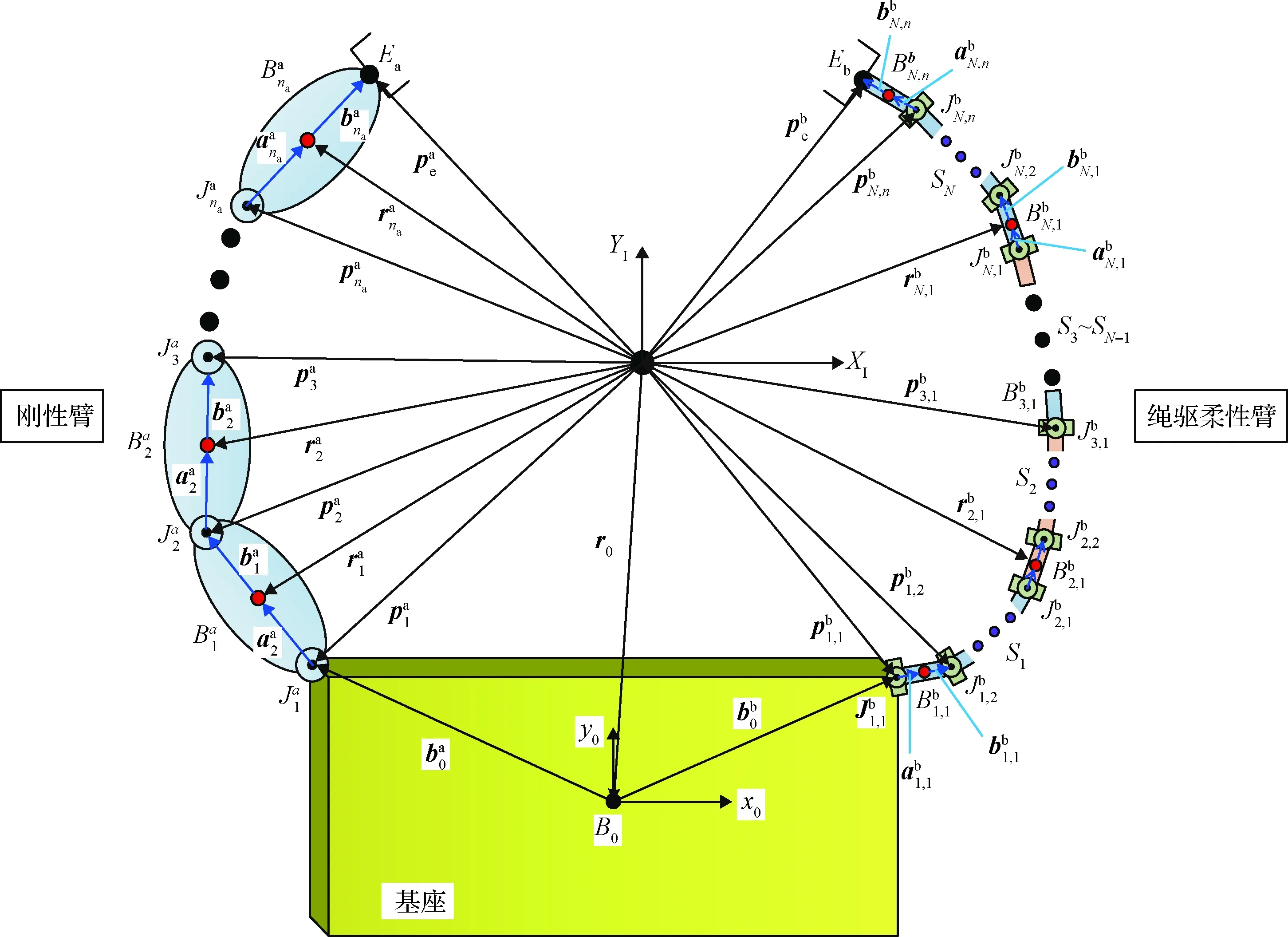
图2 混合双臂系统的广义模型Fig.2 Generalized model of the hybrid dual-arm system

(2)

根据相对运动的原理，刚性臂(Arm-a)和绳驱柔性臂(Arm-b)的末端角速度分别为

(3)

联立式(2)和式(3)可得

(4)

式中：

(5)

(6)

(7)

(8)

(9)

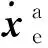
对于自由漂浮模式下的双臂空间机器人，由于没有外力、外力矩作用，系统的线动量以及角动量守恒。整个双臂空间机器人系统满足如下完整、非完整约束：

(10)

P0和L0分别为刚柔混合双臂系统初始的线动量和角动量，初始时设P0和L0为0。那么，根据式(10)可得

(11)

将式(11)代入到式(4)可得刚性臂末端、绳驱柔性臂末端与各个关节之间的映射关系,分别为

(12)

(13)

联立式(12)和式(13)可得

(14)

式中：Jg为刚柔混合双臂空间机器人的广义雅可比矩阵。

2 刚柔双臂抓持-操作协同策略与等效建模

2.1 受限空间操作任务分析及操作策略流程

本文研究的受限空间在轨操作的任务场景如图3所示。从图中可以得出，目标点位置处于狭小空间内，因此需要将结构尺寸较小的绳驱柔性臂作为主臂实现狭窄空间穿越并完成操作任务，而负载大的刚性臂作为辅臂来调节目标卫星与绳驱柔性臂的相对位置关系，从而辅助绳驱柔性臂完成上述任务操作。

图3 在轨服务任务场景Fig.3 On-orbit servicing mission scenario

本文中的狭小空间主要指狭窄平面空间，它是故障帆板与卫星主体之间的宽度仅为60 mm的缝隙区域，而目标操作点就在此区域内。因此，在对混合双臂进行协同规划时，不仅需要使得主臂(绳驱柔性臂)的末端到达期望的目标点，还需要保证主臂的各个臂段不与故障帆板和目标卫星主体发生碰撞，而主臂的各个臂杆的直径为40 mm，与狭缝的宽度相比仅有20 mm的余量，给主臂进入狭小空间内进行维修操作带来巨大的挑战。另外，为了提高主臂对故障帆板进行维修时的操作能力，还需要对主臂的可操作度进行优化从而增大主臂在任务操作方向上的可操作度。而主臂的可操作度不仅与自身的构型有关还与基座的状态、刚性臂的构型有关，这进一步增大了机械臂进入狭窄空间中进行维修操作的轨迹规划难度。因此针对以上难题，本文提出了基于受限空间可操作度优化的混合双臂协调规划方法，不仅可以使得主臂穿越狭窄平面空间完成维修任务,还能避免与故障帆板、卫星本体发生碰撞，此外还增强了机械臂的任务操作能力。

混合双臂空间机器人系统完成狭小空间作业操作的策略流程如图4所示。

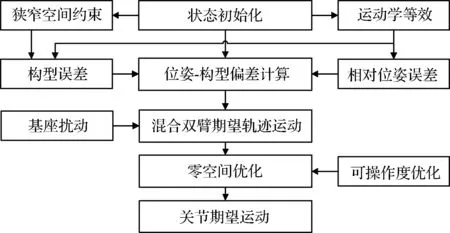
图4 受限空间操作的策略流程Fig.4 Strategy flow for the confined space operation

首先确定目标捕获时两星的初始状态及狭窄空间约束条件，并对绳驱柔性臂进行运动学等效。这里对它进行运动学等效的主要目的是实现其末端位姿和臂型的同步控制，以使其完成狭窄空间作业任务。其次，根据当前两星的相对位姿状态及狭窄空间约束条件,计算得到作业臂末端与目标点的相对位姿偏差和作业臂与狭窄平面空间的构型偏差。根据上述偏差数据规划刚柔双臂末端的期望运动，在此过程中基座处于自由漂浮状态，因此在混合双臂末端轨迹规划中也需考虑基座扰动带来的影响。然后，为了保证作业臂在完成狭窄空间作业任务的前提下还具备更大的操作能力，这里采用零空间矩阵对作业臂在受限空间操作方向上的可操作度进行优化。最后，得到经过可操作度优化后的刚柔双臂的期望关节角度。

2.2 绳驱柔性臂运动学等效后的系统建模

为了实现混合双臂系统中绳驱柔性臂的臂型控制以完成狭窄平面空间的穿越，这里对该臂进行运动学等效，具体理论及证明可详见文献[23]。可知基座漂浮状态下，绳驱柔性臂等效后的运动学模型为

(15)

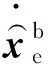
等效后的关节角度与原始绳驱柔性臂的关节角度之间的关系可表示为

g(Θb)

(16)

可得绳驱柔性臂等效后关节角速度与等效前关节角速度之间的关系

(17)

(18)

将式(17)代入到式(15)中可得

(19)

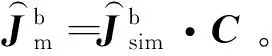
联立式(11)、式(14)和式(19)可得绳驱柔性臂运动学等效后的混合双臂系统运动学方程为

(20)

(21)

可得它的零空间投影矩阵为

(22)

3 操作度优化的协同轨迹规划方法

3.1 刚柔混合双臂末端运动规划

混合双臂开始执行狭窄空间作业任务时，混合双臂与任务目标点的相对位姿和相对臂型状态如图5所示。

图5 维修任务中混合双臂与目标点的相对状态Fig.5 Relative state between the hybrid dual-arm system and the target point in the maintenance task

此时，绳驱柔性臂末端与目标点的相对位置、相对指向和相对臂型偏差分别为：

(23)

式中：pt为目标操作点在惯性系中的位置；kt为目标操作点的指向；nt为目标操作点所在狭窄平面的法向量。

因此，规划的混合双臂末端期望速度分别为

(24)

(25)

联立式(20)、式(24)和式(25)可得

(26)

3.2 任务操作方向上可操作度优化的轨迹规划

根据式(14)可知，当基座处于自由漂浮状态时，绳驱柔性臂的运动学方程为

(27)

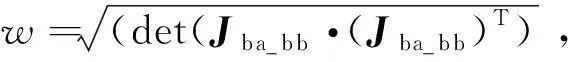
(28)

(29)

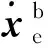
(30)

式中：γ1～γ6表示末端速度和角速度与坐标系各轴的夹角。

将式(29)代入到式(28)可得

λ2(pT·(Jba_bb(Jba_bb)T)-1·p)=1

(31)

当机械臂工作时，一般希望允许的λ值越大越好。因此，在速度方向p上的可操作度可定义为：

Mm=λ2=(pT·(Jba_bb(Jba_bb)T)-1·p)-1

(32)

需要指出的是，在式(32)中计算的可操作度综合考虑了末端线速度和角速度两个因素。而在实际的任务操作中，往往只需保证末端有足够大的线速度即可。因此在进行可操作度计算时，只需要雅可比矩阵Jba_bb的上三行数据即可。由此，设混合双臂系统中作业臂在任务操作方向为kt∈R3×1，则将式(32)中的p替换为kt，将式(32)中的Jba_bb替换为Jba_bb(1∶3,∶)，可得在kt方向上的可操作度大小为

(Jba_bb(1∶3,∶))T)-1·kt)-1

(33)

式中：Jba_bb(1∶3,∶)表示矩阵Jba_bb上三行的数据。

令κ=∂Mm/∂Θ，可得

(34)

又根据式(14)和式(26)可得，为了使刚柔混合双臂末端达到期望速度，则刚柔双臂系统中各个关节角速度应为

(35)

式中：φ为零空间的任意向量，即待优化的向量。

将式(35)代入式(34)可得

(36)

由于式(36)中的φ为任意向量，为了使作业臂在任务方向上的可操作度足够大，这里令

φ=ρκ

(37)

式中：ρ为正实数。因此将式(37)代入到式(36)，可得

(38)

(39)

4 仿真校验

4.1 仿真系统建立

仿真系统的初始状态如图6所示，该仿真系统模型通过联合仿真软件建立，然后得到相应的仿真数据和仿真动画。无偏置刚性臂的DH参数如表1所示，绳驱柔性臂的DH参数可参见文献[23]。

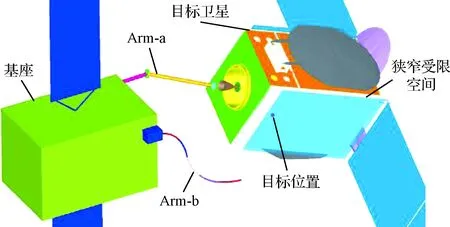
图6 仿真的初始状态Fig.6 The initial state of the simulation

表1 无偏置刚性臂的DH参数Table 1 DH parameters of the rigid arm without offset

在当前构型下，刚柔双臂的初始角度分别为：

(40)

根据等效前绳驱柔性臂的关节角度Θb，可得当前构型下绳驱柔性臂等效后的关节角度为

-7.2°, -15.3°, 6.3°, 26.5°, 2.8°]Τ

(41)

在仿真中，运动学等效前的绳驱柔性臂各个关节角的极限值为

(42)

因此，绳驱柔性臂等效后的关节角极限值为

(43)

当前构型下，目标位置向量以及目标操作方向向量在惯性系下分别为

(44)

此时目标点所在的狭窄平面空间的法向量为

(45)

4.2 仿真结果

本小节对提出的基于任务可操作度优化的刚柔混合双臂协调轨迹规划方法进行仿真分析。其中，刚性臂和绳驱柔性臂的各个时刻的期望关节角速度按照式(39)规划。这里，将系数ρ的值设置为0.5，优化向量κ的方向的计算过程如式(34)所示。

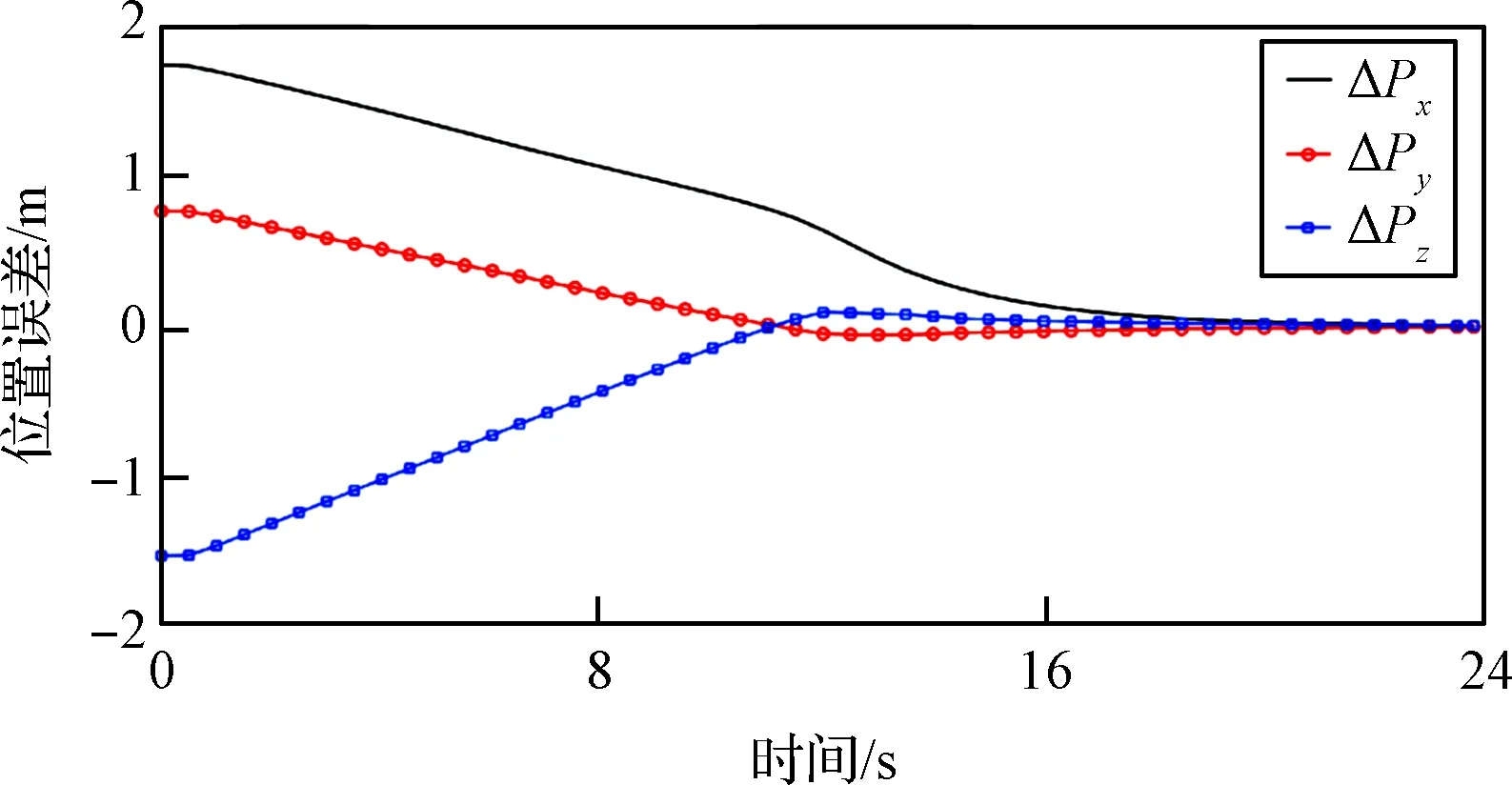
图7 仿真中的相对位置偏差Fig.7 Relative position deviation in the simulation

图8 仿真中的相对姿态偏差和构型偏差Fig.8 Relative attitude and configuration deviation in the simulation

根据仿真结果可知，仿真总时间为23.8 s。在仿真中，绳驱柔性臂与任务目标点的位置偏差曲线如图7所示，绳驱柔性臂与任务目标点的指向偏差曲线以及与受限空间的构型偏差曲线如图8所示。根据图7和图8中的仿真结果可知，在仿真的最后时刻，绳驱柔性臂与目标点的位置偏差和指向偏差为[6.75,-3.64, 6.35]mm和0.0004°，绳驱柔性臂与受限空间的构型偏差为0.0006°，上述偏差值全部小于所设定的阈值，因此可以得出：通过刚性臂和绳驱柔性臂的协同规划成功地完成了狭小空间内的作业任务。

在仿真过程中，混合双臂系统的基座处于自由漂浮状态。整个仿真过程中，基座质心的位置变化和姿态变化曲线如图9所示。仿真过程中，某些时刻的仿真系统的状态如图10所示，进一步地验证了算法的有效性。

如图11所示，给出了分别采用有可操作度优化方法和无可操作度优化方法时，任务方向上可操作度大小的变化曲线。其中，虚线表示有可操作度优化时任务方向上的可操作度，实线表示无可操作度优化时任务方向上的可操作度。

从图中可知，在仿真的任意时刻有操作度优化方法的可操作度数值要大于或等于无操作度优化时的可操作度数值。在仿真的终止时刻，有可操作度优化方法的可操作度大小为56.33，而无可操度优化方法的可操作度大小为41.19。从而可知，通过可操作度优化方法使得机械臂在进行受限空间作业时，可操作度提高了36.76%。通过计算也可得到两种方法中任务方向的平均可操作度大小，具体的计算过程如下：

(46)

式中：tf为仿真的总时间。

根据式(46)可得,采用有可操作度优化方法的平均可操作度值为68.38；无可操作度优化方法的平均可操作度值为56.76。从而可知，通过可操作度优化方法使得机械臂在进行受限空间作业的过程中，平均可操作度提高了20.49%。

图9 基座质心的位置和姿态变化曲线Fig.9 Position and attitude curves of the centroid of the base

图10 某些时刻时仿真模型的状态图Fig.10 The state of the simulation model at some moments

图11 两种方法中任务方向上的可操作度Fig.11 Manipulability in the direction of the task in both methods

5 结 论

本文建立了绳驱柔性臂运动学等效后的刚柔混合双臂模型，并推导了等效后混合双臂系统的广义雅可比矩阵以及对应的零空间投影矩阵。基于上述零空间投影矩阵建立了绳驱柔性臂可操作度优化的目标函数，同时结合广义雅可比矩阵得到了刚柔混合双臂协同执行狭窄空间作业时的期望关节角速度和关节角度。本文的主要创新点为,解决了传统算法中未考虑在轨狭小空间作业时的操作能力优化问题。通过本文方法不仅实现了绳驱柔性臂安全地穿越狭小空间，同时还提高了在任务操作方向上的操作能力，其中在终止时刻的可操作度提高了36.76%，整个任务过程中的平均可操作度提高了20.49%。