一道高考平面解析几何试题的思考与探究

王雪尧

(云南师范大学数学与统计学院，云南昆明，650500)

1 试题呈现

例1(2021年乙卷理科第21题)已知抛物线C：x2=2py(p>0)的焦点为F，且F与圆M：x2+(y+4)2=1上点的距离最小值为4.

(1)求p；

(2)若点P在M上，PA，PB是C的两条切线，A，B是切点，求△PAB面积的最大值.

本题考查平面上一点与圆上点的距离的最值、抛物线的标准方程，抛物线的几何性质，抛物线的切线，三角形面积及其最值的求法等相关知识，涉及的知识面广，综合性强.此外，该试题聚焦数学运算、逻辑推理、直观想象等数学核心素养，蕴含数形结合、函数与方程、转化与化归等数学思想方法，有效发挥了高考的选拔功能.

2 解法探究

第(1)问p=2.本文仅对第(2)问进行探究.第(2)问属于圆锥曲线中求解三角形面积的问题，解题的突破口是选择合适的方式将三角形面积表示出来，结合本题的已知条件，可采用以下几种方法解题.

由题意可得直线AB斜率存在，设其方程为y=kx+b，

Δ=(-4k)2-4×(-4b)=16k2+16b>0，x1+x2=4k，x1x2=-4b，

因为P在M上，故4k2+(4-b)2=1，即(4-b)2=1-4k2≤1，

于是-1≤4-b≤1，即3≤b≤5.故，

4k2+4b=-b2+12b-15=-(b-6)2+21.

由3≤b≤5知，当b=5时-(b-6)2+21取得最大值20.

解法2用三角形面积公式的向量坐标形式求面积

命题：设点A(x1，y1)，B(x2，y2)，C(x3，y3)，则△ABC的面积.

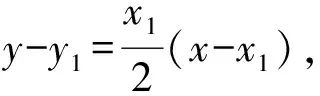
点A，B坐标满足2y-x0x+2y0=0，

所以直线AB的方程为2y-x0x+2y0=0.

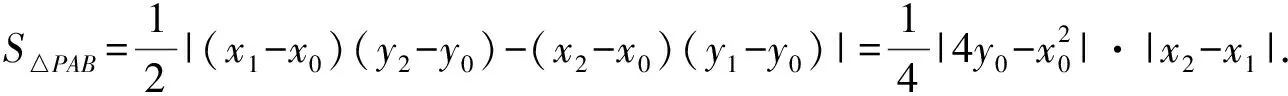
P点坐标满足：x02+(y0+4)2=1.

∴(y0+4)2=1-x02≤1∴-5≤y0≤-3.

∴x02-4y0=1-(y0+4)2-4y0=-(y0+6)2+21.

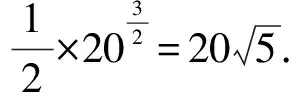
分析：该解法思路简单明了，只需直接套用命题结论并利用韦达定理进行化简，即可依据函数的单调性求出最大值，但该方法属于知识拓展性的解题策略，需要学生掌握向量方法表示的三角形面积公式，学生相对来说比较陌生.

解法3利用阿基米德三角形的性质求面积

观察图1可知，当P点位于圆偏上的位置，如P′，A′、B′两点在抛物线靠下方，此时开口小，A、B两点间的距离小；让P点沿圆顺时针旋转，发现，当P点位于圆偏下的位置，如P″，A″、B″两点在抛物线靠上方，此时开口大，A、B两点间的距离大.所以，当P点位于圆的最下方，即圆与y轴的交点(0，-5)时，此时A，B间的距离最大.

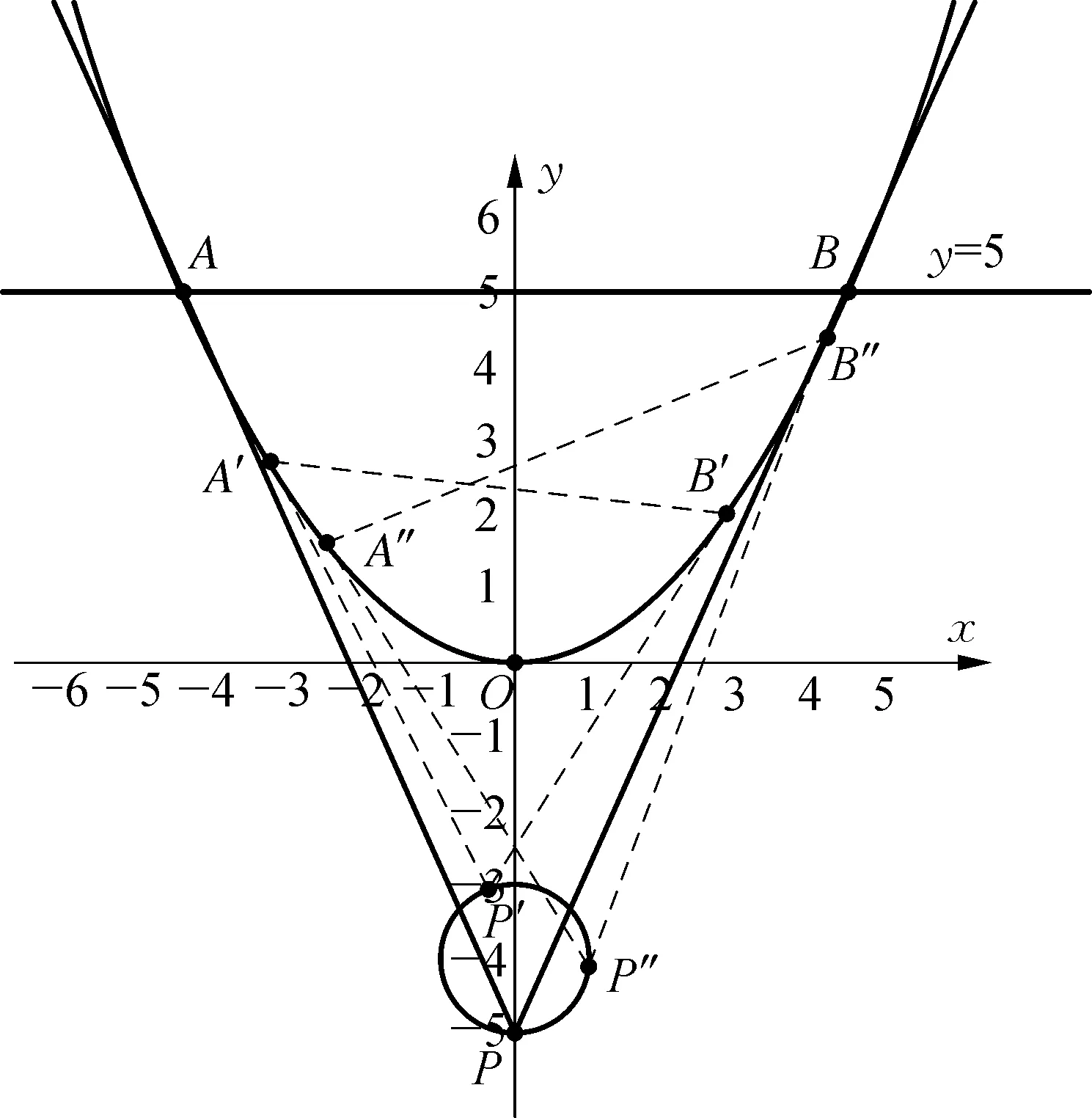
图1

解：P点坐标为(0，-5)时，△PAB的面积最大.

由极点极线原则[1]可知P为极点，AB为极线，AB的直线方程为y=5.

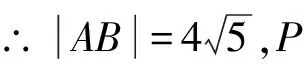
分析：利用阿基米德三角形的性质，由图可直观得出三角形面积取最大值时点P的坐标，进而得出面积的最大值，显示了阿基米德三角形的“威力”，体现了数形结合的思想.若学生了解阿基米德三角形的相关性质，该题的解答将手到擒来.

该解法揭示了本题的背景知识——阿基米德三角形，抛物线弦的两个端点以及在这两端点处的切线的交点所构成的三角形就称为阿基米德三角形.阿基米德三角形具有深厚的背景和丰富的内涵，高考命题者对此图形青睐有加.阿基米德三角形的相关性质也是命题者的热点素材，在高考试题中屡见不鲜，如2019年全国3卷理科第21题、2006年全国2卷理第21题、2012年江西(理)第21题、2013年辽宁(理)第21题.“对该三角形的性质作进一步的研究对于提高学生对抛物线几何性质的认识以及培养他们的数学美学意识是必要的、有益的.”[2]

3 教学建议

3.1 研究背景知识，拓宽解题思路

高考试题具有较深的背景知识，但由于不了解试题背景，学生在解题过程中可能会出现解题思路不简洁、解题方法不优化等解题障碍，加强试题背景知识的学习可以拓宽学生的解题思路、优化解法方法，还能加深学生对知识发生发展过程的理解，增强学习热情与信心.因此在教学中，教师要深入挖掘试题背景知识，进一步分析研究背景知识，引导学生探究拓展学习，使学生掌握更多的解题方法.此外，追根溯源是加强背景知识学习的有效途径.教师应多钻研高等数学知识，用“高观点”来研究中学数学，厘清知识的来龙去脉，以便能将知识深入浅出地教授给学生.

3.2 落实核心素养，渗透思想方法

“不管平面解析几何试题的背景知识是什么，落脚点都在考查学生的基本思想方法与能力，关注的不是学生对背景知识的熟悉程度，而是学生核心素养的落实.”[3]不管高考试题怎样千变万化，都是以考查基础知识与基本方法为落脚点的，都是聚焦核心素养的落实，发挥其选拔的功能.特别地，对于平面解析几何试题，聚焦学生的“转化与化归、数形结合、探索实践”等基本思想方法和能力，关注的是“数学运算、逻辑推理、直观想象”等核心素养的落实.在教学中，教师要着重培养学生的“四基”“四能”，关注数学核心素养的有效落实，体现数学学科的全面育人价值和创新应用价值.

3.3 提倡一题多解，优化解题方法

教师在平时的解题教学中，不能盲目采用“题海战术”，而应该追求试题的典型性与拓展性，讲清楚试题的内涵与外延，提倡一题多解，寻求最优解题方法.在数学解题教学中，要引导学生深入分析题目的条件与结论，从不同角度不断挖掘二者之间的联系，尽可能多的发现问题的不同解法，并分析哪种解法是最优且有效的，经过这样的训练，有助于学生快速发现问题的不同解法并选择最优且有效的方法解题；其次是在解题教学中要注重引导学生总结解题方法.考查某一个知识点的题目千变万化，但万变不离其宗，要帮助学生透过现象看本质，分析问题特征，不断总结解题经验，通过解一道题就会解一类题，达到举一反三的教学效果；最后要关注问题情境，对学生进行变式训练，从而提高学生应对多变问题情境的能力，发展思维的灵活性.